1. T Chen, B Dai, D Liu, J Song, and Z Liu, "Velodyne-based curb detection up to 50 meters away," In:
Proceedings of 2015 IEEE Intelligent Vehicles Symposium (IV); Seoul, South Korea. 2015, pp 241ŌĆō248.

2. M Tan, B Wang, Z Wu, J Wang, and G Pan, "Weakly supervised metric learning for traffic sign recognition in a LIDAR-equipped vehicle,"
IEEE Transactions on Intelligent Transportation Systems, vol. 17, no. 5, pp. 1415ŌĆō1427, 2016.

3. S Kim, D Oh, and J Lee, "Joint DFT-ESPRIT estimation for TOA and DOA in vehicle FMCW radars,"
IEEE Antennas and Wireless Propagation Letters, vol. 14, pp. 1710ŌĆō1713, 2015.

4. MS Lee, V Katkovnik, and YH Kim, "System modeling and signal processing for a switch antenna array radar,"
IEEE Transactions on Signal Processing, vol. 52, no. 6, pp. 1513ŌĆō1523, 2004.

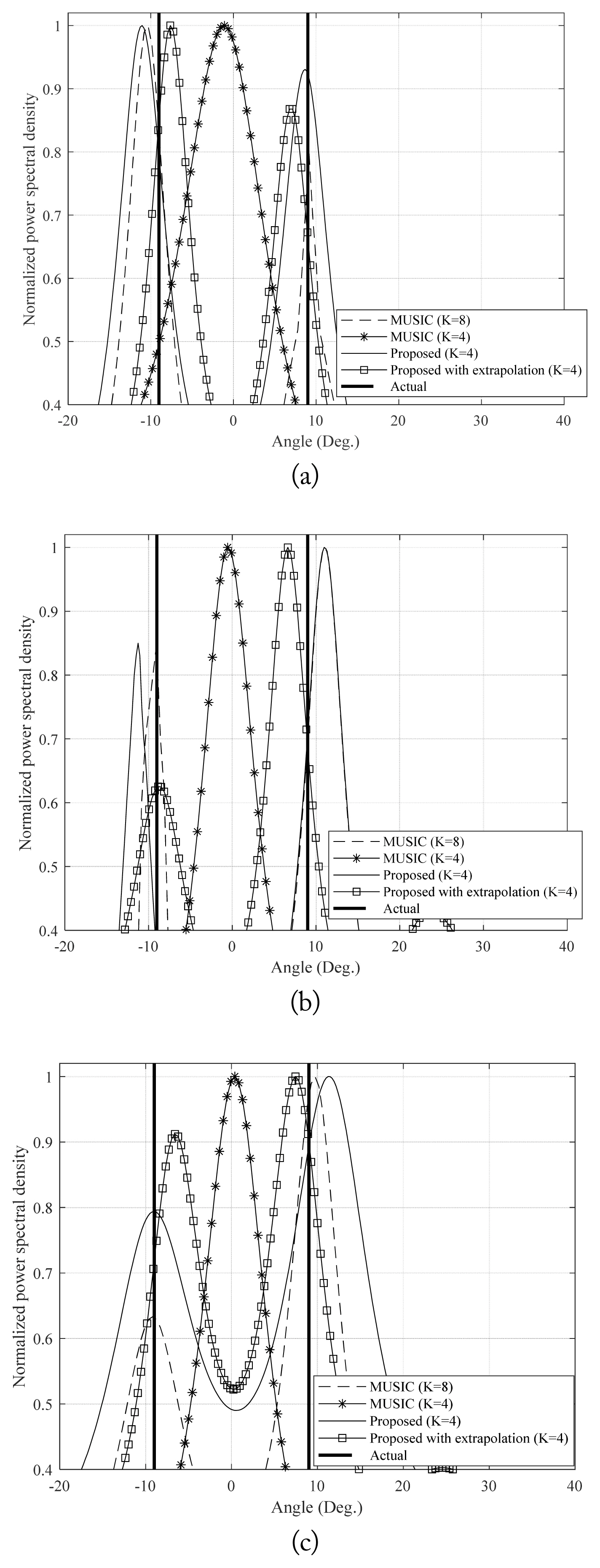
5. S Kim and KK Lee, "Low-complexity joint extrapolation-MUSIC-based 2-D parameter estimator for vital FMCW radar,"
IEEE Sensors Journal, vol. 19, no. 6, pp. 2205ŌĆō2216, 2019.

6. S Saponara and B Neri, "Radar sensor signal acquisition and multidimensional FFT processing for surveillance applications in transport systems,"
IEEE Transactions on Instrumentation and Measurement, vol. 66, no. 4, pp. 604ŌĆō615, 2017.

7. F Wan, WP Zhu, and MNS Swamy, "Spacial extrapolation-based blind DOA estimation approach for closely spaced sources,"
IEEE Transactions on Aerospace and Electronic systems, vol. 46, no. 2, pp. 569ŌĆō582, 2010.

8. VK Nguyen, MD Turley, and GA Fabrizio, "A new data extrapolation approach based on spectral partitioning,"
IEEE Signal Processing Letters, vol. 23, no. 4, pp. 454ŌĆō458, 2016.

9. Z Peng, JM Munoz-Ferreras, Y Tang, C Liu, R Gomez-Garcia, L Ran, and C Li, "A portable FMCW interferometry radar with programmable low-IF architecture for localization, ISAR imaging, and vital sign tracking,"
IEEE Transactions on Microwave Theory and Techniques, vol. 65, no. 4, pp. 1334ŌĆō1344, 2017.

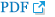
10. Z Peng, L Ran, and C Li, "A K-band portable FMCW radar with beamforming array for short-range localization and vital-Doppler targets discrimination,"
IEEE Transactions on Microwave Theory and Techniques, vol. 65, no. 9, pp. 3443ŌĆō3452, 2017.

11. M Nosrati, S Shahsavari, S Lee, H Wang, and N Tavassolian, "A concurrent dual-beam phased-array Doppler radar using MIMO beamforming techniques for short-range vital-signs monitoring,"
IEEE Transactions on Antennas and Propagation, vol. 67, no. 4, pp. 2390ŌĆō2404, 2019.

12. Y Huang, Y Zhang, W Li, Y Zhang, and Z Wang, "Angular super resolution for scanning radar with music based on virtual array mapping," In:
Proceedings of 2015 IEEE Radar Conference (RadarCon); Arlington, VA. 2015, pp 0324ŌĆō0328.

13. B Kim, S Kim, and J Lee, "A novel DFT-based DOA estimation by a virtual array extension using simple multiplications for FMCW radar,"
Sensors, vol. 18, no. 5, pp. 1560ŌĆō1576, 2018.



14. BW Choi, EH Bae, JS Kim, and KK Lee, "Improved prewhitening method for linear frequency modulation reverberation using dechirping transformation,"
The Journal of the Acoustical Society of America, vol. 123, no. 3, pp. EL21ŌĆōEL25, 2008.


15. F Belfiori, W van Rossum, and P Hoogeboom, "Coherent MUSIC technique for range/angle information retrieval: application to a frequency-modulated continuous wave MIMO radar,"
IET Radar, Sonar & Navigation, vol. 8, no. 2, pp. 75ŌĆō83, 2014.

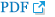
16. S Kim and K Lee, "A low complexity based spectrum partitioning-ESPRIT for noncontact vital radar,"
Elektronika ir Elektrotechnika, vol. 23, no. 2, pp. 54ŌĆō58, 2017.