I. Introduction
Electromagnetic metamaterials (MTMs) [1] are broadly defined as artificial and effectively homogeneous electromagnetic structures with unusual properties not readily available in nature. MTMs enable the generation of left-handed waves through effective negative permittivity and permeability. MTMs have various applications, such as lens, absorber, and cloak, among others [2ŌĆō4].
However, MTMs have a limitation when applied to radio frequency (RF) devices because they are lossy and have a narrow bandwidth (BW) in the microwave frequency range. To overcome these problems, the composite right-/left-handed (CRLH) transmission line (TL) was introduced [5]. Many miniaturized antennas, power dividers, resonators, filters, and couplers [6ŌĆō12] can be designed and applied for many RF applications using CRLH TLs. However, until now, no detailed investigation on the positive/negative nth-mode resonance frequency and its BW of N unit cell CRLH TL has been conducted as far as we know.
This study defines the negative mode and provides the guideline for designing a resonance antenna using the CRLH TL. The physical resonance mechanism can be explained by using the circuit model. Specifically, the difference between the negative and positive modes can be clearly seen, and the physical meaning of the negative mode is explained. Moreover, by deriving the analytic expression of the negative/positive nth mode resonance frequency to show the correlation between the BW and the dispersion curve slope, this study provides the guideline for easily designing a resonance antenna.
II. Resonance Mechanism of the Negative/Positive nth Mode of the N Unit Cell CRLH TL
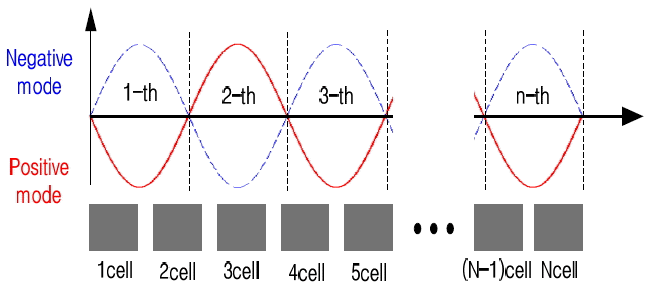
Fig. 1 shows the current distribution of the positive/negative nth mode for N cells with an open boundary condition at both ends. For the nth mode, because the total electrical length is a multiple of ŽĆ with an open-ended boundary, the nŽĆ/N phase delay is expected to occur per unit cell when n = 0, ┬▒1, Ōŗ», ┬▒ NŌĆō1, and the current distribution has n time variations of a standing wave pattern for both the positive and negative modes. The length of one variation corresponds to a half wavelength of each mode. Therefore, both the nth positive and negative modes have the same wavelength (or the same magnitude of a propagation constant) even though the corresponding frequencies are different because of different dispersion branches. However, the phase difference between the positive and the negative mode is 180┬░ because of the opposite direction of the propagation direction between the two modes. The phase difference of 180┬░ is easy to understand from the current standing wave pattern with an open boundary condition at both ends given by
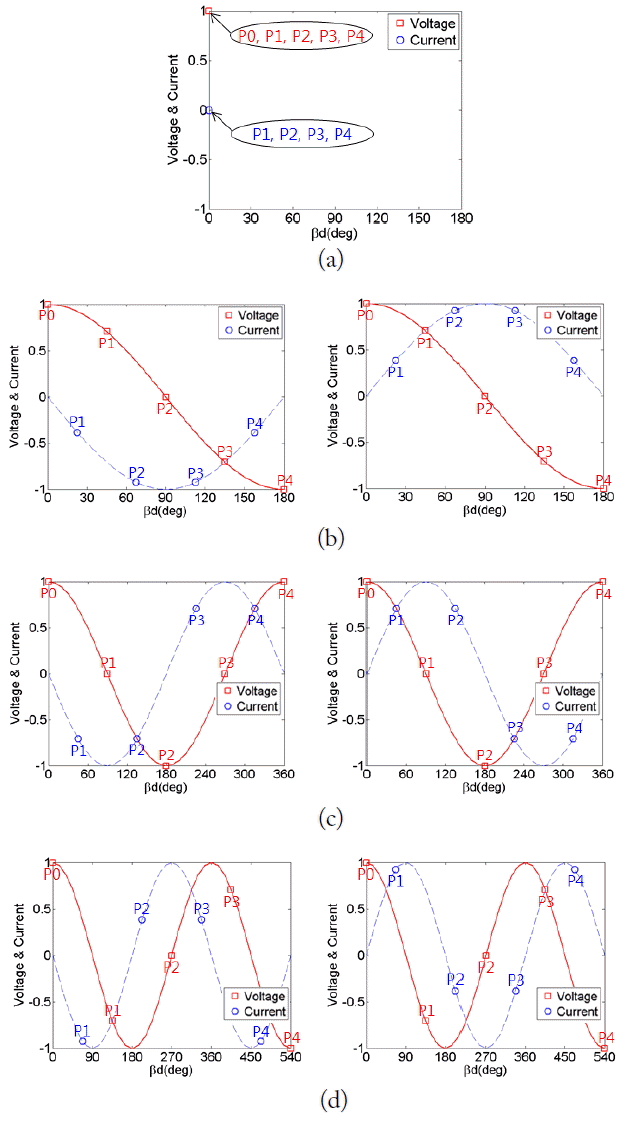
To confirm the illustration in Fig. 1, the current distribution of the N unit cell CRLH TL with an open boundary condition is simulated with the Advanced Design System (Fig. 2). If a lossless structure with no resistance exists, only the magnitude of the reactance will distribute the amplitude of the current and the voltage. For N = 3, the voltages and the currents of each node in Fig. 2 are measured with probes labeled P0, 1, 2, Ōŗ», N and compared (Fig. 3).
The magnitude of the voltage and the current is normalized to 1, and the current flowing in the ŌłÆz direction is a (+) sign. The left column of Fig. 3 shows the positive modes and the right column shows the negative modes. The result indicates that the voltage and the current have a cosine and sine distribution, respectively, except for the 0th mode.
For the 0th mode, no current flows and the voltage operates without a phase delay because of the zero value of Yp. The 0th-order resonance with an open-ended boundary condition occurs at the shunt resonance (Yp = 0). Moreover, the number of half wavelength variations increases as the mode number of n increases. When the distributions of the positive and negative modes are compared, note that the current distribution changes to 180┬░ in the phase as discussed previously, and the voltage distribution is the same as that in the open boundary condition.
In terms of the circuit, the P0 probe is fixed at +1 Vdc at the input node. Therefore, its amplitude is +1 V regardless of the mode. For the positive mode, Yp/2 has a positive value because CR is predominant over LL; for the negative mode, Yp/2 has a negative value because LL is predominant over CR. Therefore, the direction of the current changes in the negative mode. The reason for the existence of negative modes is that they are another combination that makes the total input reactance zero. In other words, Zs and Yp of the negative mode have the same ratio as Zs and Yp of the positive mode. The only difference is that the signs of Im(Zs) and Im(Yp) of the negative mode are negative and those of Im(Zs) and Im(Yp) of the positive mode are positive. Fig. 3 satisfies the condition of
1 / L L C R > 1 / L R C L 1 / L L C R 1 / L R C L 1 / L R C L
III. Derivation of Resonance Frequency
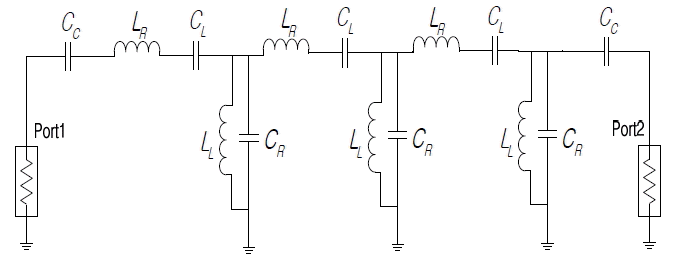
The unit cell of CRLH TL can be drawn as an equivalent T circuit as shown in Fig. 4.
The following relation can be obtained by using the phase difference (╬Ė = nŽĆ/N) between two terminals:
where N is the number of total unit cells, and n is the number of arbitrary unit cells.
Eq. (3) is represented by a matrix. When it is compared with the ABCD matrix, the following equation is obtained:
As Eq. (4) has a non-trivial solution and the circuit in Fig. 4 is reciprocal (AD ŌĆō BC = 1), we can summarize both as Eq. (5):
where
Eq. (5) is a quartic equation for Žē. By substitution into a quadratic equation, the following equation can be obtained:
where
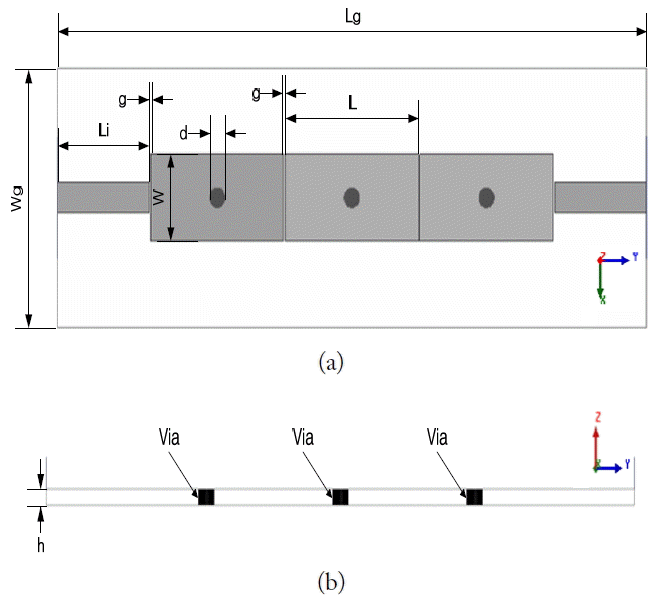
To confirm the result of Eq. (6), the resonance frequencies of the three-unit cell CRLH TL are calculated using the circuit simulation of Ansoft Designer and the full wave simulation of HFSS. Fig. 5 is the electrically coupled three-unit cell CRLH equivalent circuit employed in the circuit simulation. Fig. 6 shows the mushroom structure, and Fig. 5 illustrates its parameters (CR, LR, CL, and LL) and their values. The structure in Fig. 6 is obtained from [13] and simulated by High Frequency Structure Simulator (HFSS). Table 1 compares the resonance frequencies of the three-unit cell CRLH TL obtained from Eq. (6), HFSS, and Ansoft Designer, respectively.
Table 1 shows that the results obtained by Eq. (6), and all the data in Table 1 are obtained with an unbalanced condition. The circuit simulation is almost the same as expected. However, the results from HFSS have some differences in the resonance frequencies caused by the errors of the extracted parameters (CR, LR, CL, and LL) from the real structure. The method of parameter extraction from the dispersion curve inevitably cannot produce perfect matched results in all modes. However, the overall results are in good agreement.
IV. Correlation between Slope and BW
The slope of the dispersion curve df/d╬Ė (╬Ė = electrical length per unit cell) is a measure of how much the frequency changes as the electrical length changes. The higher the slope is, the greater the frequency changes even with a change in electrical length. In other words, a large value of
1 d ╬Ė / d f
(7)
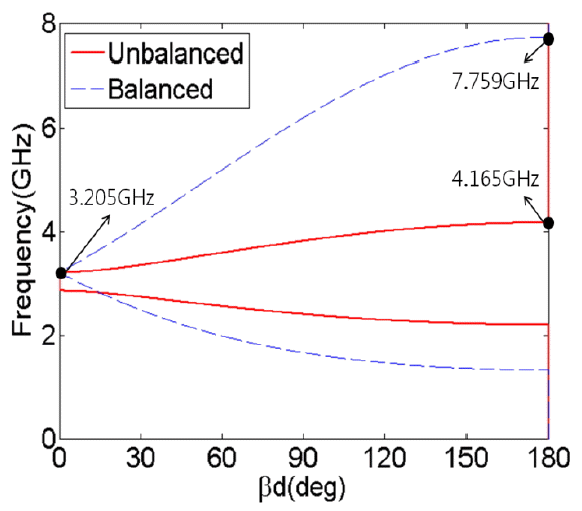
In Tables 2 and 3, the dimensions of slope and BW are in MHz/┬░ and MHz, respectively. Except for the 0th mode of the unbalanced condition, Tables 2 and 3 show that the slope is always closely related to the BW. Fig. 7 illustrates that the BW, which is correlated with the dispersion curve slope, is significantly improved when the balanced condition is satisfied [14]. In other words, the overall BW improves because the average slope from 0┬░ to 180┬░ increases from 5.3 MHz/┬░ to 25.3 MHz/┬░. This finding can be confirmed by comparing Tables 2 and 3.
V. Conclusion
This study has successfully derived the analytic expression for the positive/negative nth-mode resonance frequency of an N unit cell CRLH transmission line. The resonance mechanism of the nth positive/negative mode is investigated by the current distribution of an N unit cell CRLH transmission line. Both the positive and the negative nth resonance modes have n times current variation, but their phase difference is 180┬░. The slope of the CRLH dispersion curve is closely correlated with the BW. When the CRLH TL is designed with a balanced condition, the BW increases from the slope.