Investigation of Single-Input Multiple-Output Wireless Power Transfer Systems Based on Optimization of Receiver Loads for Maximum Efficiencies

Sejin Kim; Sungyoun Hwang; Sanghoek Kim; Bomson Lee

doi:10.26866/jees.2018.18.3.145

J. Electromagn. Eng. Sci > Volume 18(3); 2018 > Article

Kim, Hwang, Kim, and Lee: Investigation of Single-Input Multiple-Output Wireless Power Transfer Systems Based on Optimization of Receiver Loads for Maximum Efficiencies

Regular Paper

Journal of Electromagnetic Engineering and Science 2018;18(3):145-153.

Published online: July 31, 2018

DOI: https://doi.org/10.26866/jees.2018.18.3.145

Investigation of Single-Input Multiple-Output Wireless Power Transfer Systems Based on Optimization of Receiver Loads for Maximum Efficiencies

Sejin Kim, Sungyoun Hwang, Sanghoek Kim, Bomson Lee^*

Department of Electronics and Radio Engineering, Kyung Hee University, Yongin, Korea

^*Corresponding Author: Bomson Lee (e-mail: bomson@khu.ac.kr)

Received September 25, 2017 Revised November 15, 2017 Accepted March 7, 2018

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this paper, the efficiency of single-input multiple-output (SIMO) wireless power transfer systems is examined. Closed-form solutions for the receiver loads that maximize either the total efficiency or the efficiency for a specific receiver are derived. They are validated with the solutions obtained using genetic algorithm (GA) optimization. The optimum load values required to maximize the total efficiency are found to be identical for all the receivers. Alternatively, the loads of receivers can be adjusted to deliver power selectively to a receiver of interest. The total efficiency is not significantly affected by this selective power distribution. A SIMO system is fabricated and tested; the measured efficiency matches closely with the efficiency obtained from the theory.

Keywords: Efficiency, Multiple-Input Multiple-Output System, Multiple Receivers, Optimum Loads, Wireless Power Transfer

I. Introduction

Wireless power transfer (WPT) technology has been actively studied and developed over the past several years and is considered to be one of the most important and promising key techniques to find widespread application in the forthcoming IT industries. Many products related to single-input single-output (SISO) WPT systems, such as charging units for mobile phones and home appliances, are already available in commercial markets. Most of them are based on the inductive or resonant operating mode [1]; the latter is expected to gain more support from the market because it enables an extended power transfer range [2]. Various studies have been conducted focusing on higher efficiencies or longer transfer ranges. For example, WPT systems with a slab of metamaterial were studied for a stronger near-field coupling between two resonant coils [3]. Recently, the multiple-input multiple-output (MIMO) WPT technology has drawn attention of researchers and industries, particularly with the growing interest in the energy autonomy of the Internet of Things (IoT) sensors [4–7]. Although general analyses about MIMO WPT systems are found in literature, their characteristics have been usually examined in detail for some special cases of SIMO or MISO systems [8–13]. From circuit modeling analysis, Bou-Balust et al. [8] claimed that in SIMO systems, the total system efficiency can significantly improve as the number of receivers increases. In another SIMO-related approach [9], the conventional four-coil structure was extended to accommodate a multiple-receiver system with an example of one sending coil, one receiving coil, and two load coils. In [10], the effects of transmit diversity were investigated both analytically and through simulations for the power transfer with multiple transmitters (MISO). The power transfer efficiencies and distribution of magnetic fields were analyzed for a system of multiple misaligned transmitters and a single receiver. In [11–13], a method of providing adjustable power distribution for multiple receivers was presented with an upper bound of efficiency. This work, however, adopted a simplifying assumption that the optimum loads of the receivers are proportional to their internal loss resistances with a constant proportionality ratio.

In the present study, various features of SIMO systems are examined with closed-form optimum loads to maximize the total system efficiency. We demonstrate that the optimum loads are identical for all receivers without the assumption made in [11]. Our results are somewhat different from [8] in that the total efficiency of SIMO systems does not increase significantly as the number of receivers increases. The optimal loads obtained from the closed-form solution are validated with the genetic algorithm (GA) optimization results. Lastly, the theoretical efficiencies with the optimal loads used in this study are compared with electromagnetic simulation and measurement results; they show good agreement with each other.

This paper is organized as follows. In Section II, general MIMO WPT systems are formulated on the basis of circuit theory, and the important behaviors of a typical SISO system are summarized for the purpose of reference. In Section III, the cases of a SIMO system with one transmitter and multiple receivers are analyzed in detail in terms of efficiencies and coupling coefficient interpretations. The total efficiency of typical SIMO systems is shown not to change much as the number of receivers increases. This enables controlled power distribution among the receivers without changing the total efficiency considerably. In Section IV, some important findings of this work are summarized with conclusions.

II. Modeling of MIMO Wireless Power Transfer System

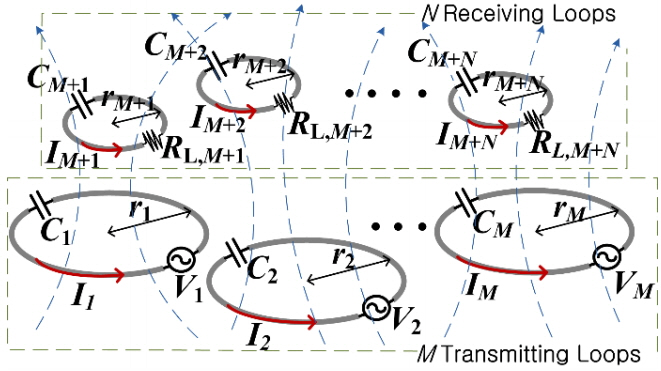
Fig. 1 shows a typical MIMO WPT system, with M transmitters and N receivers. All the loops have some inductances and resistances. We assume that each loop is loaded with a capacitor to resonate at a specific design frequency. In addition, we assume that the M transmitters are excited by voltage sources and that N receivers have extra load resistances to receive transferred powers. Once the sizes and positions of the transmitters and receivers are specified, the coupling coefficients can be determined in a straightforward manner [14, 15]. Then, the WPT system can be analyzed in various aspects. The general MIMO WPT system is commonly analyzed using Z-matrix formulation [16, 17]. The Z matrix as a function frequency is given by

(1)

[V1⋯VM0⋯0]=[Z11⋯Z1,M⋯Z1,M+N⋯ ⋯ZM,1 ZM,M+NZM+1,1 ZM+1,M+N⋯ ⋯ZM+N,1⋯ ⋯ZM+N,M+N] [I1⋯IMIM+1⋯IM+N].

In (1), the first M elements in the column matrix [V] are the supplied voltages. The supplied voltages V_n (= |V_n| ∠ θ_n, n = 1, 2, ···, M) may be complex numbers in general. The principal diagonal elements of [Z] are expressed as

(2)

Zn,n=Rn+jω0Ln (ωω0-ω0ω)

for n = 1, 2, ···, M and

(3)

Zn,n=Rn+RLn+jω0Ln (ωω0-ω0ω)

for n = M + 1, M + 2, ···, M + N, where is the common angular resonant frequency of each loop, R_n’s are the loop resistances, L_n’s are the loop self-inductances, ω₀L_n’s are the reactance slope parameters of the loop resonator, and R_Ln’s are the extra load resistances for the receivers. The other elements of [Z] are given by

(4)

Zm,n=-jωMm,n=-jωkm,nLmLn (m≠n)

for m, n = 1, 2, ···, M, M + 1, ···, M + N, where M_m_,_n and k_m_,_n ’s are the mutual inductances and coupling coefficients between two loops, respectively [18].

When all the elements of the Z-matrix are given, the current at each loop is determined by [I] = [Z]⁻¹[V]. Then, the total input power and the received power at each receiver are given by

(5)

Pin=∑n=1M12Re[VnIn*]

and

(6)

PLn=12RLn|In|2(n=M+1,M+2,⋯,M+N).

The efficiency at the n^th receiver is defined as

(7)

ηn=PLnPin(n=M+1,M+2,⋯,M+N)

and the total efficiency is the sum of (7) and given by

(8)

ηt=∑n=M+1M+Nηn.

Once all the elements of the Z-matrix in (1), including V_n ’s, R_n’s, and R_Ln’s for a MIMO system, are specified, the WPT efficiencies can be easily evaluated at a design frequency ω₀ using (5)–(8). Commonly, we aim to maximize (7) or (8). For this purpose, we may decide the values of R_Ln’s by either an analytical or some numerical optimization methods. In this study, we focus on SIMO WPT systems and obtain closed-form solutions for the optimal loads.

Before we analyze SIMO WPT systems in various configurations, we review a SISO system for reference. In a SISO system (M = 1, N = 1), the WPT efficiency η₂ is compactly expressed [19] as

(9)

η2 (F21,b2)=F212(1+b21+F212)(1+1b21+F212)

where b₂ (= R_L2/R_L2,opt) is the load deviation factor with respect to the optimum (R_L2,opt), which is [20]

(10)

RL2,opt=R21+F212.

In (9) and (10), F21 (=k21Q21=k21Q2Q1) is the figure of merit for the SISO system. Some notable features from (9) are as follows: when b₂ = 1 (R_L2 = R_L2,opt) in (9), the system is at the optimum state and the efficiency touches the upper bound. When b₂ > 1 or b₂ < 1, the system is in the under-coupled or the over-coupled region, respectively, and the efficiencies are lower than the maximum. Explicitly, the efficiency degrades symmetrically with the deviation of b₂ from unity in a log scale. For example, with b₂ = 10 or 1/10, the efficiency degrades in a same rate from (9). Likewise, whether when b₂ → ∞ (open-circuited or under-coupled limit) or when b₂ → 0 (short-circuited or over-coupled limit), η₂ → 0. Lastly, when F₂₁ → ∞ or 0, η₂ → 1 or 0 irrespective of b₂ as long as b₂ has a finite value.

III. Various Configurations in SIMO System

1. SIMO System with M = 1 and N = 2

Consider the case of a SIMO system with M = 1 and N = 2 shown in Fig. 2. One Tx loop and two Rx loops may be randomly positioned according to the required system configuration. If the coupling coefficients between the two receiving loops (k₂₃) are negligibly small compared with k₂₁ and k₃₁, we may assume k₂₃ = 0 and can express the efficiencies for Rx 2 (η₂) and for Rx 3 (η₃) as

(11)

η2 (β2,β3)=β2(1+β2).F212[1+β2+F212+(1+β2)(1+β3)F312]

and

(12)

η3 (β2,β3)=β3(1+β3)·F312[1+β3+F312+(1+β3)(1+β2)F212]

as functions of β₂ and β₃, which are the normalized load resistances defined by R_L₂/R₂ and R_L₃/R₃, respectively. F₂₁ and F₃₁ are the figures of merit given by k21Q2Q1 and k31Q3Q1, respectively. The approximations (11) and (12) are relatively accurate as long as F23≤F212 or F312. Observing η₂ in (11), we see that as β₃ → ∞ (open-circuited) or F₃₁ → 0 (Rx 3 placed far away from Tx 1, for example), the role of Rx 3 vanishes and (11) can be shown to reduce to (9) [19, 20]. The total efficiency η_t is the sum of (11) and (12), and is given by

(13)

ηt (β2,β3)=η2+η3.

To find the optimum normalized load β_2,_opt with which η₂ is maximized for a fixed β₃, we require

(14)

∂η2 (β2,β3)∂β2=0

which is solved to give

(15)

β2,opt=RL2,optR2=1+F212+F3121+β31+F3121+β3.

In (15), we can see that the normalized optimum load β_2,_opt depends on β₃. Especially when β₃ → ∞ (open-circuited) or F₃₁ → 0 (Rx 3 placed far way), the system practically behaves like a SISO and β_2,_opt becomes 1+F212 to be consistent with (10). Similarly, the optimum load to maximize η₃ for a fixed β₂ is

(16)

β3,opt=RL3,optR3=1+F312+F2121+β21+F2121+β2.

On the other hand, to find the optimum loads with which the total efficiency η_t (13) is maximized, the following two equations should be satisfied simultaneously:

(17)

∂ηt (β2,β3)∂β2=0

and

(18)

∂ηt (β2,β3)∂β3=0.

The solution of (17) and (18) can be shown to be

(19)

β2,opt=β3,opt=1+F122+F132.

It turns out that β_2,_opt is equal to β_3,_opt. For some illustrations with respect to the SIMO system in Fig. 2, we assume that r₁ = 15 cm, r₂ = r₃ = 5 cm (which is chosen to represent the size of typical mobile phones), the radius of each loop ring (r_ring) is 0.2 cm, and the resonant frequency (f₀) is 6.78 MHz.

In Fig. 3, we plot the efficiencies as a function of β₂ and β₃ using (11), (12), and (13). The center positions of one Tx and two Rx loops are (0, 0, 0), (0, −15, 10), and (0, 7.5, 25), respectively. The Q-factors of Tx 1, Rx 2, and Rx 3 are 730, 630, and 630, respectively. For this example, F₂₁ = 11 and F₃₁ = 5.8. Fig. 3(a) and (b) show that when β₂ is about 4 and β₃ → ∞, η₂ is maximized to 0.82. Meanwhile, when β₂ → ∞ and β₃ is approximately 2, η₃ is maximized to 0.52. The maximum total efficiency η_t in Fig. 3(c) is about 0.85 when β₂ and β₃ are about 12, as expected by (19). Note that while the efficiencies η₂ and η₃ significantly vary depending on β₂ and β₃, the total efficiency η_t is rarely sensitive as long as they are greater than approximately 4. This is an interesting property of SIMO systems since the efficiency for each receiver may be properly distributed considering the charged battery energy levels of the receivers while the total remains unchanged.

Fig. 4 shows η₂, η₃, and η_t for different center positions (0, 10, v) of loop 3 (Rx 3) in Fig. 2. For this example, the centers of loop 1 (Tx 1) and loop 2 (Rx 2) are fixed at (0, 0, 0), (0, −10, 15), respectively. At each position of Rx 3, β_2,_opt and β_3,_opt given by (19) are shown in Fig. 4. Alternatively, β₂ and β₃ can be optimized to maximize the fitness function η_t (8) using the GA in MATLAB based on (1)–(7). The optimized β₂ and β₃ are in good agreement with β_2,_opt and β_3,_opt obtained by (19). This demonstrates the validity of (19). In the GA optimization of this study, all the coupling effects are considered.

2. SIMO System with one Tx and N Rx’s (Same Receiving Loops Are Symmetrically Positioned)

Now, we consider a more general case of the SIMO system, where all the N Rx loops are identical and symmetrically located around one Tx loop. From the symmetry of the system, the figure of merit (F = kQ) between the Tx and Rx loops should also be identical. When the coupling coefficients between the Rx loops are negligibly small, the total efficiency η_t and the efficiency for each loop η can be expressed as

(20)

ηt=Nη(b,F)=NF2(1+b1+NF2)(1+1b1+NF2)

where b (= R_L/R_L_,_opt) is the load deviation factor from the optimum load resistance, given as

(21)

RL,opt=R1+NF2.

The expressions (20) and (21) are the extensions of (9) and (10) for the SISO system. When N = 1, (20) and (21) reduces to (9) and (10), respectively.

Table 1 shows the optimum load resistances (R_L,opt) for different number of receivers. Again, the solutions from GA optimization are consistent with the closed-form solution in (21), validating the formulations. As the separation between the Tx and Rx loops increases, the figure of merit (F) and the optimum load R_L_,_opt usually become very small, as exemplified in Table 1. Ideally, these small optimum resistances can be transformed to the 50 Ω impedance of typical receivers using a feeding loop. In practice, we may use a multi-turn Rx loop to increase the optimum resistance enough to make it directly match practical receivers [21].

Fig. 5(a) shows a SIMO system (M = 1, N = 4) with four symmetrically placed receivers. The Tx loop is centered at the origin. The vertical and horizontal distances of each Rx loop from the origin are v and h, respectively. Fig. 5(b) shows the fabricated SIMO system based on Fig. 5(a). Additional feeding loops for the Rx loops were used for 50-Ω matching to measure the S-parameters using a network analyzer. Table 2 shows the approximated [21, 22] and measured values of circuit elements. The measured values were obtained using the Keysight E5063A VNA. The measured resistances were about two times the theoretical ones. This has been a usual phenomenon due to oxidization of copper wires [23]. On the other hand, the inductances and capacitances are in close agreement. The measured Q of the transmitting loop and receiving loops are approximately 330 and 234, respectively.

Fig. 6 shows the efficiencies for different numbers (N) of Rx loops in the SIMO system. The resonant frequency (f₀) is 6.78 MHz, r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, the radius of each loop (r_ring) is 0.2 cm, v = 7.5 cm, and h = 15 cm in connection with Fig. 5.

The solid lines are obtained from the GA optimization using the measured circuit values summarized in Table 2. The dashed lines show the efficiencies from the closed-form expression (20). The square symbols show the measured efficiencies using a two-port network analyzer (Fig. 5). It is shown that as the number of Rx loops (N) increases, the total efficiency (η_t) increases to some extent. The efficiency (η_n) for each Rx loop is roughly the total efficiency (η_t) divided by the number of Rx loops N. The efficiencies obtained by the numerical calculations using the GA method, closed-form expressions, and measurements are all in good agreement. In Table 3, we summarize the coupling coefficients between the Tx and Rx loops and between two adjacent Rx loops for different numbers (N) of receivers from 1 to 4 with the configurations described in Figs. 5 and 6. As we have first assumed, the coupling coefficients between the Tx and Rx loops are considerably larger than those between the two adjacent Rx loops. This explains why the efficiencies obtained from the closed-form expressions (20) and (21), neglecting the coupling coefficients between the two adjacent Rx loops, agree well with those obtained from the numerical optimization and measurements.

3. SIMO System with M = 1 and N = 4 (Same Receiving Loops, But Not Symmetrically Positioned)

To analyze the effects of placing the Rx loops over the transmitter with different densities, we have evaluated the efficiencies for three configurations (cases A, B, and C) as shown in Fig. 7. The angles of the two Rx loops seen from the origin are 90°, 60°, and 41° for cases A, B, and C, respectively. For all the three cases, r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, the radius of the loop ring is 0.2 cm, h = 15 cm, and the Rx loops are placed right above the Tx loop with a vertical distance of v.

In Fig. 8(a), we show the total efficiencies η_t obtained using GA as the vertical distance v increases. The system has been optimized to maximize η_t’s for each case. The total efficiency for case A is shown to decrease approximately from 88% to 50% as v increases from 2 cm to 24 cm. The total efficiency for case C is 3%–10% lower than that for case A due to the effect of the stronger mutual couplings between the Rx loops. In Fig. 8(b), η₂ (= η₅) for case C is shown to be the highest, and η₃ (= η₄) for case C is shown to be the lowest and to approach zero when v is about 25 cm. The differences of η₂ and η₃ increase as v increases for case B. This is due to the effects of the mutual coupling between the Rx loops becoming relatively stronger as v increases.

In Fig. 9, the optimum load resistances (R_L,opt) are obtained from GA and plotted as a function of v for the three cases. The optimum load resistances R_L₂_,opt (= R_L_5,_opt) for all of the three cases are shown to decrease as expected when v increases. On the other hand, R_L_3,_opt (= R_L_4,_opt) for case C shows a tendency to increase due to the effect of the strongest mutual coupling between Rx loops.

In Table 4, we show the coupling coefficients for cases A, B, and C. The minus sign implies that the magnetic flux lines generated from one Rx loop cross the other Rx loop in an opposite direction and may counter the flux lines coming from the Tx loop. The coupling coefficients between the Rx loops do not change depending on v. However, as v increases from 1 cm to 25 cm, the coupling coefficient between the Tx loop and any of the Rx loops (k₂₁ = k₃₁ = k₄₁ = k₅₁) decreases from 0.0357 to 0.006. The absolute value of k₃₂ for case C is the largest (= 0.0654), which is even larger than k_n₁ (= 0.0357) for n = 2–5. Therefore, the efficiency η₃ (= η₄) for case C is the lowest.

Fig. 10 shows the geometry of case D where Rx 5 moves outward from the center. The horizontal distance of Rx 5 is h₅. For this case, r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, and the radius of the Rx loop ring is 0.2 cm. In Fig. 11(a) and (b), the efficiencies and the optimum load resistances obtained using GA are shown as a function of h₅. The optimum load resistances have been obtained using the GA to maximize the total efficiencies (η_t) for each h₅ with all mutual couplings considered. In Fig. 11(a), we can see that η_t’s do not change much as h₅ increases from 0 to 26 cm. It only decreases from 87% to 80%. However, the efficiency of each receiver does change significantly. Obviously, η₅ decreases most dramatically from 64% to a few percent. Instead, η₂ (= η₄) and η₃ are shown to increase from about 10% to 26%. One important observation is that the total efficiency can be maintained rather steady while the efficiency for each receiver changes considerably.

IV. Conclusion

Various features of WPT SIMO systems have been investigated on the basis of a more general MIMO system formulation. Useful closed-form expressions for the efficiencies and optimum loads for SIMO systems have been derived and their validity was checked through GA optimization and measurement. The results of this study have provided physical insight that can be employed to any practical SIMO WPT systems and have demonstrated the feasibility of SIMO systems in the range of tens of centimeters with sufficient design examples.

ACKNOWLEDGEMENTS

This research was supported by the Ministry of Science, ICT and Future Planning, Korea, under the Information Technology Research Center support program (No. IITP-2018-2016-0-00291) supervised by the IITP (National IT Industry Promotion Agency).

Fig. 1

A general configuration of a MIMO WPT system with M transmitters and N receivers.

Fig. 2

A SIMO system with M = 1 and N = 2.

Fig. 3

Efficiencies as a function of the normalized load resistances β₂ and β₃ in a SIMO system: (a) η₂, (b) η₃, and (c) η_t. M = 1, N = 2, r₁ = 15 cm, r₂ = r₃ = 5 cm, r_ring = 0.2 cm, F₂₁ = 11, F₃₁ = 5.8, the centers of Tx and Rx loops are (0, 0, 0), (0, −15 cm, 10 cm), and (0, 7.5 cm, 25 cm), respectively.

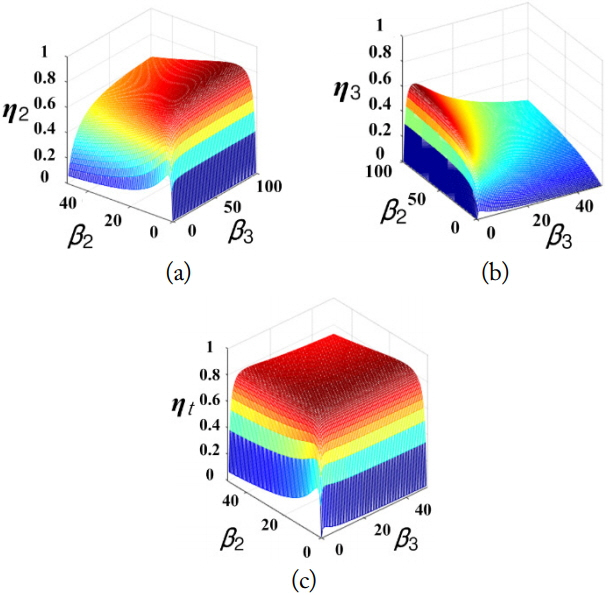
Fig. 4

Efficiencies for different positions (0, 10, v) of Rx 3 and fixed positions of Tx 1 and Rx 2 at (0, 0, 0) and at (0, −10 cm, 15 cm), respectively (r₁ = 15 cm, r₂ = r₃ = 5 cm, r_ring = 0.2 cm and R₂ = R₃ = 0.017 Ω).

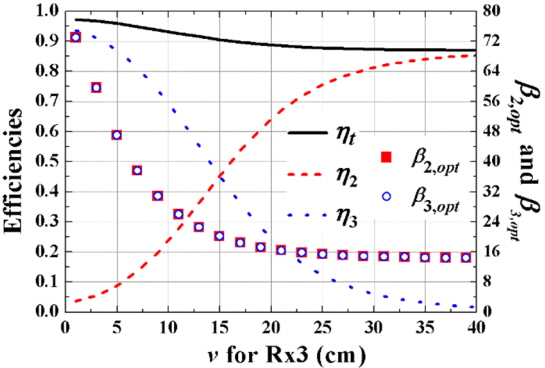
Fig. 5

SIMO system (M = 1, N = 4) with symmetrically placed receivers. (a) SIMO geometry and (b) photograph of fabricated SIMO structure.

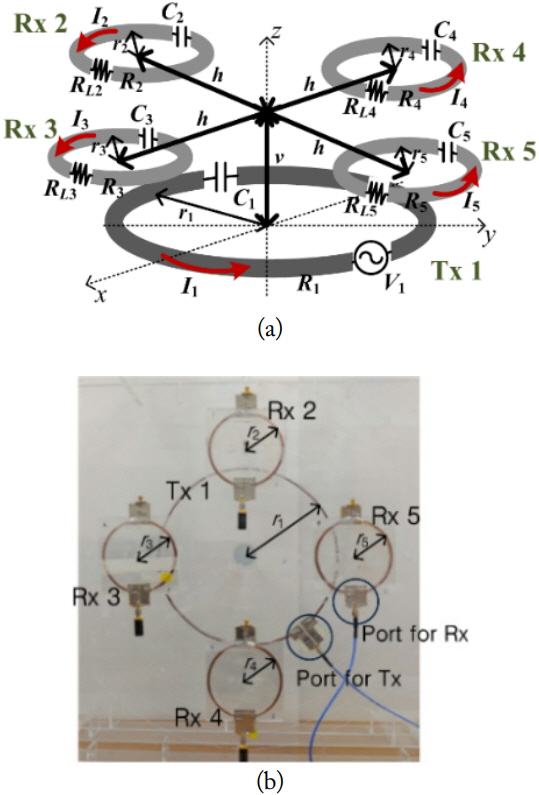
Fig. 6

WPT efficiencies depending on the number of Rx loops (N) in the SIMO system (r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, v = 7.5 cm, h = 15 cm, k₂₁ = k₃₁ = k₄₁ = k₅₁ = 0.02072).

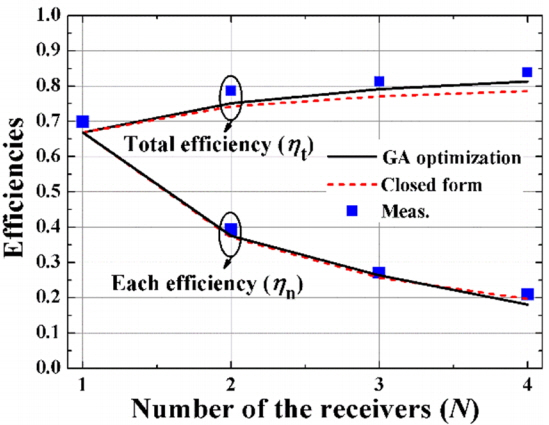
Fig. 7

Three special cases of SIMO system (M = 1, N = 4) with un-symmetrically placed receivers (r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, h = 15 cm, and v is the vertical distance between T×1 and each Rx loop).

Fig. 8

WPT efficiencies obtained using GA as a function of v (Fig. 5) in the SIMO system for cases A, B, and C (r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm). (a) Total efficiencies η_t and (b) each efficiency η_n for n = 2–5.

Fig. 9

Optimum load resistances (R_L,opt) obtained using GA as a function of v (Fig. 5) in the SIMO system for cases A, B, and C (r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm).

Fig. 10

SIMO system (M = 1, N = 4) where one Rx loop (Rx 5) moves outward from the center (r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, v is the vertical distance between T×1 and each Rx loop).

Fig. 11

Efficiencies and optimum load resistances obtained using GA for the SIMO system in Fig. 10 (M = 1, N = 4). (a) Efficiencies by h_r×₅ and (b) optimum load resistances by h_r×₅. r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, v = 7.5 cm.

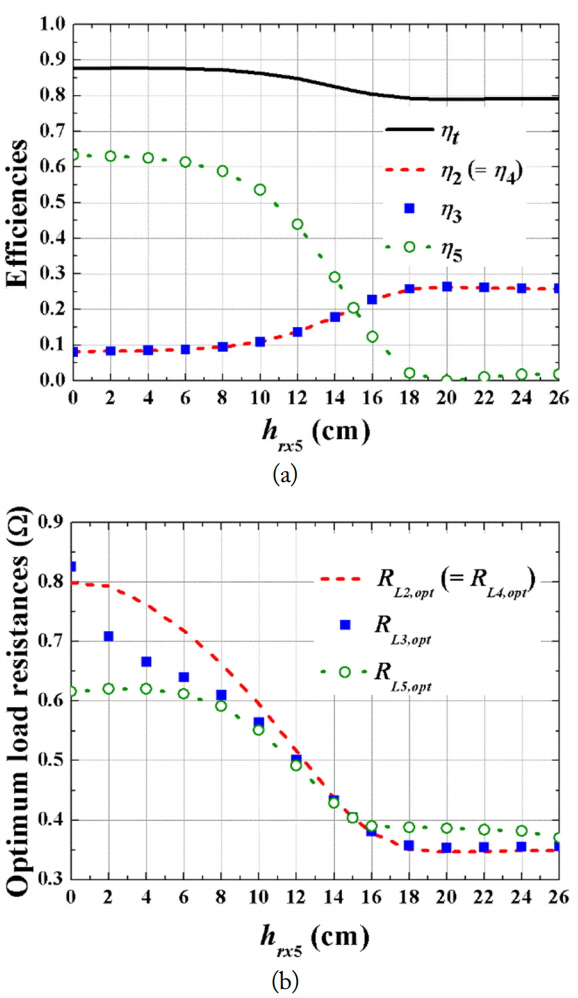
Table 1

Optimum load resistances (R_L,opt)

Number of Rx loops	GA optimization (Ω)	Closed-form (21) (Ω)
1	0.202	0.202
2	0.282	0.282
3	0.346	0.344
4	0.409	0.397

The receivers are symmetrically placed h = 15 cm and v = 7.5 cm.

Table 2

Approximated and measured circuit values

Circuit elements	Approximated [21, 22]	Measured
R₁ (Ω)	0.051	0.11
R₂–R₅ (Ω)	0.017	0.04
L₁ (μH)	0.876	0.853
L₂–L₅ (μH)	0.223	0.22
C₁ (nF)	0.629	0.646
C₂–C₅ (nF)	2.472	5.5
Q₁	730	330
Q₂–Q₅	560	234

Table 3

Coupling coefficients for the SIMO system with N symmetrically placed receivers

	N = 1	N = 2	N = 3	N = 4
k_n₁ (n = 2–5)	0.02072	0.02072	0.02072	0.02072
k₃₂	-	−0.00116	−0.00183	−0.00352
k₄₂	-	-	−0.00183	−0.00116

r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, v = 7.5 cm, h = 15 cm.

Table 4

Coupling coefficients between the Rx loops for three cases

	Case A	Case B	Case C
k_n₁ (n = 2–5)	0.0357 → 0.006 as v increases from 1 cm to 25 cm
k₃₂	−0.00352	−0.01180	−0.06536
k₄₂	−0.00116	−0.00183	−0.00452
k₅₂	-	−0.00116	−0.00174

r₁ = 15 cm, r₂ = r₃ = r₄ = r₅ = 5 cm, r_ring = 0.2 cm, h = 15 cm.

REFERENCES

1. PS Riehl, A Satyamoorthy, H Akram, YC Yen, JC Yang, B Juan et al., "Wireless power systems for mobile devices supporting inductive and resonant operating modes," IEEE Transactions on Microwave Theory and Techniques, vol. 63, no. 3, pp. 780–790, 2015.

2. P Dubal, "Rezence: wireless charging standard based on magnetic resonance," International Journal of Advanced Research in Computer and Communication Engineering, vol. 4, no. 12, pp. 198–200, 2015.

3. B Wang, W Yerazunis, and KH Teo, "Wireless power transfer: metamaterials and array of coupled resonators," Proceedings of the IEEE, 2013;vol. 101, no. 6, pp. 1359–1368.

4. Q Xu, H Wang, Z Gao, ZH Mao, J He, and M Sun, "A novel mat-based system for position-varying wireless power transfer to biomedical implants," IEEE Transactions on Magnetics, vol. 49, no. 8, pp. 4774–4779, 2013.

5. K Na, H Jang, SK Oruganti, and F Bien, "An improved wireless power transfer system with adaptive technique for implantable biomedical devices," In: Proceedings of 2013 IEEE MTT-S International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-BIO); Singapore. 2013;pp 1–3.

6. SYR Hui, W Zhong, and CK Lee, "A critical review of recent progress in mid-range wireless power transfer," IEEE Transactions on Power Electronics, vol. 29, no. 9, pp. 4500–4511, 2014.

7. TM Hayslett, T Orekan, and P Zhang, "Underwater wireless power transfer for ocean system applications," In: Proceedings of OCEANS 2016 MTS/IEEE Monterey; Monterey, CA. 2016;pp 1–6.

8. E Bou-Balust, AP Hu, and E Alarcon, "Scalability analysis of SIMO non-radiative resonant wireless power transfer systems based on circuit models," In: Proceedings of 2015 IEEE International Symposium on Circuits and Systems (ISCAS); Lisbon, Portugal. 2015;pp 694–697.

9. Y Zhang, T Lu, Z Zhao, F He, K Chen, and L Yuan, "Employing load coils for multiple loads of resonant wireless power transfer," IEEE Transactions on Power Electronics, vol. 30, no. 11, pp. 6174–6181, 2015.

10. K Lee and DH Cho, "Diversity analysis of multiple transmitters in wireless power transfer system," IEEE Transactions on Magnetics, vol. 49, no. 6, pp. 2946–2952, 2013.

11. K Lee and DH Cho, "Analysis of wireless power transfer for adjustable power distribution among multiple receivers," IEEE Antennas and Wireless Propagation Letters, vol. 14, pp. 950–953, 2015.

12. YJ Kim, D Ha, WJ Chappell, and PP Irazoqui, "Selective wireless power transfer for smart power distribution in a miniature-sized multiple-receiver system," IEEE Transactions on Industrial Electronics, vol. 63, no. 3, pp. 1853–1862, 2016.

13. KE Koh, TC Beh, T Imura, and Y Hori, "Impedance matching and power division using impedance inverter for wireless power transfer via magnetic resonant coupling," IEEE Transactions on Industry Applications, vol. 50, no. 3, pp. 2061–2070, 2014.

14. SI Babic and C Akyel, "Calculating mutual inductance between circular coils with inclined axes in air," IEEE Transactions on Magnetics, vol. 44, no. 7, pp. 1743–1750, 2008.

15. G Kim and B Lee, "Alternative expressions for mutual inductance and coupling coefficient applied in wireless power transfer," Journal of Electromagnetic Engineering and Science, vol. 16, no. 2, pp. 112–118, 2016.

16. HD Lang, A Ludwig, and CD Sarris, "Magnetic near-field focusing and optimal wireless power transfer," In: Proceedings of 2015 IEEE Wireless Power Transfer Conference (WPTC); Boulder, CO. 2015;pp 1–3.

17. S Kim and B Lee, "Analysis of efficiencies for multiple-input multiple-output wireless power transfer systems," Journal of Electromagnetic Engineering and Science, vol. 16, no. 2, pp. 126–133, 2016.

18. S Raju, R Wu, M Chan, and CP Yue, "Modeling of mutual coupling between planar inductors in wireless power applications," IEEE Transactions on Power Electronics, vol. 29, no. 1, pp. 481–490, 2014.

19. C Kim and B Lee, "Analysis of magnetically coupled wireless power transmission for maximum efficiency," Journal of the Korean Institute of Electromagnetic Engineering and Science, vol. 11, no. 3, pp. 156–160, 2011.

20. G Kim and B Lee, "Analysis of magnetically coupled wireless power transfer between two resonators based on power conservation," In: Proceedings of 2014 IEEE Wireless Power Transfer Conference (WPTC); Jeju Island, Korea. 2014;pp 231–234.

21. J Kim and YJ Park, "Approximate closed-form formula for calculating ohmic resistance in coils of parallel round wires with unequal pitches," IEEE Transactions on Industrial Electronics, vol. 62, no. 6, pp. 3482–3489, 2015.

22. G Kim and B Lee, "Alternative expressions for mutual inductance and coupling coefficient applied in wireless power transfer," Journal of Electromagnetic Engineering and Science, vol. 16, no. 2, pp. 112–118, 2016.

23. A Kurs, A Karalis, R Moffatt, JD Joannopoulos, P Fisher, and M Soljacic, "Wireless power transfer via strongly coupled magnetic resonances," Science, vol. 317, no. 5834, pp. 83–86, 2007.

Biography

Sejin Kim received the B.S. degree in Electronics and Radio Engineering from Kyung Hee University, Yongin, Korea, in 2015. She is currently pursuing a master’s degree in Electronics and Radio Engineering from Kyung Hee University. Her fields of research include wireless power transfer systems, passive devices, small antennas, RFID reader antennas, and metamaterials.

Biography

Sanghoek Kim received the B.S. degree with a double major in Electrical Engineering and Mathematics from Seoul National University, Seoul, Korea, in 2007, and the M.S. and Ph.D. degrees in electrical engineering from Stanford University, CA, USA, in 2013. His research focuses on applications of radio-frequency technology and electromagnetics theory in wireless power transfer, communications, and signal integrity in high-speed channels. After graduation, he has worked at Qualcomm Inc. as a signal/power integrity engineer and in SiBeam Inc., as a millimeter-wave system engineer. Currently, he is an assistant professor in the Department of Electronics and Radio Engineering in Kyung Hee University.

Biography

Sungyoun Hwang received the B.S. degree in Information and Communication Engineering from Soonchunhyang University, Asan, Korea, in 2015. He is currently pursuing a master’s degree in Electronics and Radio Engineering from Kyung Hee University. His fields of research include wireless power transfer systems, passive devices, and small antennas.

Biography

Bomson Lee received the B.S. degree in Electrical Engineering from Seoul National University, Seoul, Korea, in 1982. From 1982 to 1988, he was with the Hyundai Engineering Company Ltd., Seoul, Korea. He received the M.S. and Ph.D. degrees in Electrical Engineering from the University of Nebraska, Lincoln, NE, USA, in 1991 and 1995, respectively. In 1995, he joined the faculty at Kyung Hee University, where he is currently a professor in the Department of Electronics and Radio Engineering. From 2007 to 2008, he was the chair of the technical group for microwave and radiowave propagation in KIEES (Korea Institute of Electromagnetic Engineering & Science). In 2010, he was an Editor-in-Chief of the Journal of the Korean Institute of Electromagnetic Engineering and Science. Since 2015, he has been a vice-chairman in KIEES. His research activities include microwave antennas, RFID tags, microwave passive devices, wireless power transfer, and metamaterials.