I. Introduction
It is difficult to use a feature vector, such as a scattering center, for target classification because although a radar using a low-frequency band has a long maximum detection range, it suffers from a narrow bandwidth. The resonance frequency is a feature vector that can overcome the limitation of narrow bandwidth and that can be well observed at low frequencies. Moreover, the resonance frequency does not theoretically change with the aspect angle, and the lower the frequency becomes, the more suitable it is to be used as the feature vector of the low-frequency radar. Previous studies that used the resonance frequency as a feature vector, performed target classification using a generalized likelihood ratio test (GLRT) [1], studied target identification using the resonance frequency extracted via the extinction-pulse (E-pulse) technique [2], studied target identification using the resonance frequency extracted via the combination of the E-pulse technique and singular value decomposition (SVD)-Prony method [3], and studied target classification using the resonance frequency extracted using the matrix pencil method (MPM) [4]. However, when only the resonance frequency is used as the feature vector, the signal in the early-time region is not used. Because the signal in the early-time region is larger in amplitude than that in the late-time region, it is inefficient not to use the signal in the early-time region. Previous research [5] extracted the waveform structure-based feature vectors in the early-time region and the resonance frequency feature vectors in the late-time region. The target classification experiment was then performed by fusing these feature vectors. Other fusion techniques are presented in [6, 7].
Although the scattering center is mainly used as the feature vector of the early-time region [8], it is difficult to extract it due to the narrow bandwidth in the case of low-frequency radar; therefore, the feature vector based on the waveform structure is used. This feature vector based on the waveform structure can overcome the range resolution problem caused by the narrow bandwidth and does not require an accurate signal model for the waveform [9].
To improve the radar target classification performance, we proposed a two-level feature vector fusion method that combines the abovementioned feature vectors of the early-time and late-time regions into the radar structure. The proposed method can obtain considerable information about the target by performing fusion in various radar structures while using both the early-time and late-time region feature vectors.
We used the electromagnetic analysis tool FEKO in the HF band (2–28 MHz) to simulate the target 3D full-scale model to obtain the radar cross section (RCS). After generating the time domain signal from the obtained RCS, the feature vector based on the waveform structure was obtained in the early-time region. In the late-time region, the resonance frequency extracted using the late-time evolutionary programming (EP)-based CLEAN algorithm [10] was used as the feature vector. After fusing the above two feature vectors in the first-level, we fuse them again between the monostatic and bistatic structures in the second-level. Then we performed the target classification experiments through the neural network classifiers. From the results, we know that the proposed two-level feature vector fusion method has the best target classification performance.
II. Feature Vectors in the Early- and Late-Time Regions
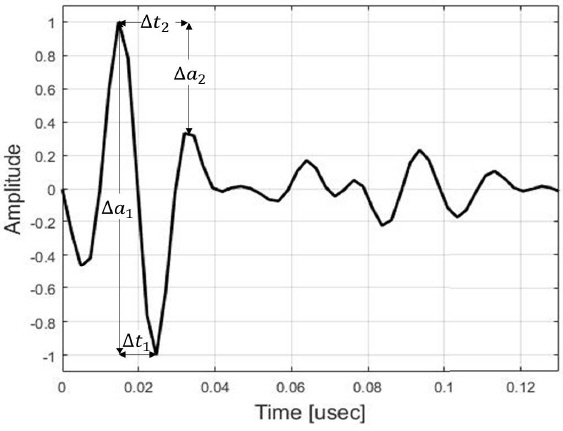
Recent developments in stealth technology with low-RCS have prompted research on detection technology. Radar absorbing material (RAM) used in low-RCS aircraft can be ineffective by using low-frequency radar [11]. Note that the resonance frequency becomes stronger as the frequency becomes lower. The resonance frequency is a feature found in the late-time region of the radar-received signal, and theoretically, does not change with the aspect angle. However, if the target classification experiment is performed only with the feature vector of the late-time region, the signal in the early-time region, which has the larger amplitude than the signal in the late-time region, cannot be considered. Therefore, it is better to use the early-time region signal together with the late-time region signal when performing the target recognition experiment. In the early-time region, the scattering center is used as the feature vector. However, because the bandwidth is limited in the low-frequency band, it is difficult to use the scattering center as the feature vector because of the range resolution problem. This problem can be solved by using the feature vector based on the waveform structure. This feature vector is the time and magnitude intervals between the maximum and minimum values of the early-time region, and the time and amplitude intervals between the maximum and second-largest values [5]. This is illustrated in Fig. 1.
A study [5] shows the fusion of the feature vectors of the early-time and late-time regions extracted using the abovementioned method. The fusion method shows better performance than the methods using only the early-time feature vector or late-time feature vector. The early-time region feature vector based on the waveform structure is shown in Eq. (1):
The late-time region feature vector is the resonance frequency extracted by the EP-based CLEAN algorithm. In general, the response in the late-time domain of the radar signal can be expressed by Eq. (2) using the singularity expansion method (SEM).
In Eq. (2)sm = σm + jωm denotes mth resonance frequency, am denotes the amplitude of the mth resonance frequency, and φm denotes the phase. TF is the time at which the late time region ends, and M is the number of resonance frequencies in the late time response. In this paper, we use the resonance frequency extracted by the EP-based CLEAN algorithm as the feature vector of the late time domain. The detailed EP-based CLEAN algorithm is as follows.
Step 1 is the initialization step. First, set m = 1. m is the repeated index value for the mth resonance frequency extraction, and the measured or calculated late time response is defined as xm(tk) where k = 1,2,…, K, and K is the number of time samples.
Step 2 is the parameter extraction step. Here, we extract the values of am, σm, ωm, and φm that minimize the cost function Jm as shown in Eq. (3) using the EP subroutine.
Here, when the sufficient number of generations has elapsed, the EP subroutine is terminated.
Step 3 is the component removal step. The component of the resonance frequency extracted in Step 2 is removed from xm(tk) to obtain the signal xm+1(tk) as shown in Eq. (4).
Step 4 is a termination confirmation step. After setting m = m + 1, if the desired M resonance frequencies are extracted, the algorithm is terminated. If not, the process returns to Step 2 and the process is repeated. As a result, the late-time EP-based CLEAN algorithm is a technique that iteratively extracts the parameters of Eq. (3) through the EP optimization technique. In this paper, parameters for two resonance frequencies are extracted according to these steps. The feature vectors of the late-time domain are as follows.
III. Feature Vector Fusion in Radar Structure
The radar structure can be divided into a monostatic structure, in which the transmitter and receiver are the same, and a bistatic structure, in which the transmitter and receiver are separated from each other. The general radar structure is a monostatic structure, in which various target recognition experiments are carried out. When an aircraft is designed with a stealth design, the back-scattering signal is reduced due to diffuse reflection. Therefore, in this case, the monostatic radar is difficult to detect; consequently, the use of bistatic radars is more effective. Previous studies on bistatic radars have been performed at Hannam University [12], which compared and analyzed the target classification performance at three bistatic angles (60°, 90°, and 150°). However, by considering only one radar structure, either monostatic or bistatic, enough information about the target cannot be utilized. Another previous study [8] showed improved target recognition performance by extracting scattering centers using fast Fourier transform (FFT)-based CLEAN [13] at each radar structure and combining them of monostatic and bistatic structures. In that study, experiments were performed on various bistatic angles, rather than one bistatic angle, to find the optimum bistatic angle with the best recognition performance.
IV. Two-Level Feature Fusion Method
This paper proposes a two-level feature vector fusion method. Here, a feature vector is fused in two steps. The first-level feature vector fuses an early-time region feature vector with a late-time region feature vector. The second-level feature vector fuses a monostatic feature vector with a bistatic feature vector. We performed experiments at three bistatic angles of 30°, 90°, and 150° to find the bistatic angle that exhibits the best target classification performance. The detailed two-level feature vector fusion method is as follows. The feature vector of the early-time region based on the waveform structure and the late-time region feature vector are fused as shown in Eq. (6):
Next, the first-level feature vectors obtained at monostatic and bistatic structure by Eq. (6) are fused once more as shown in Eq. (7):
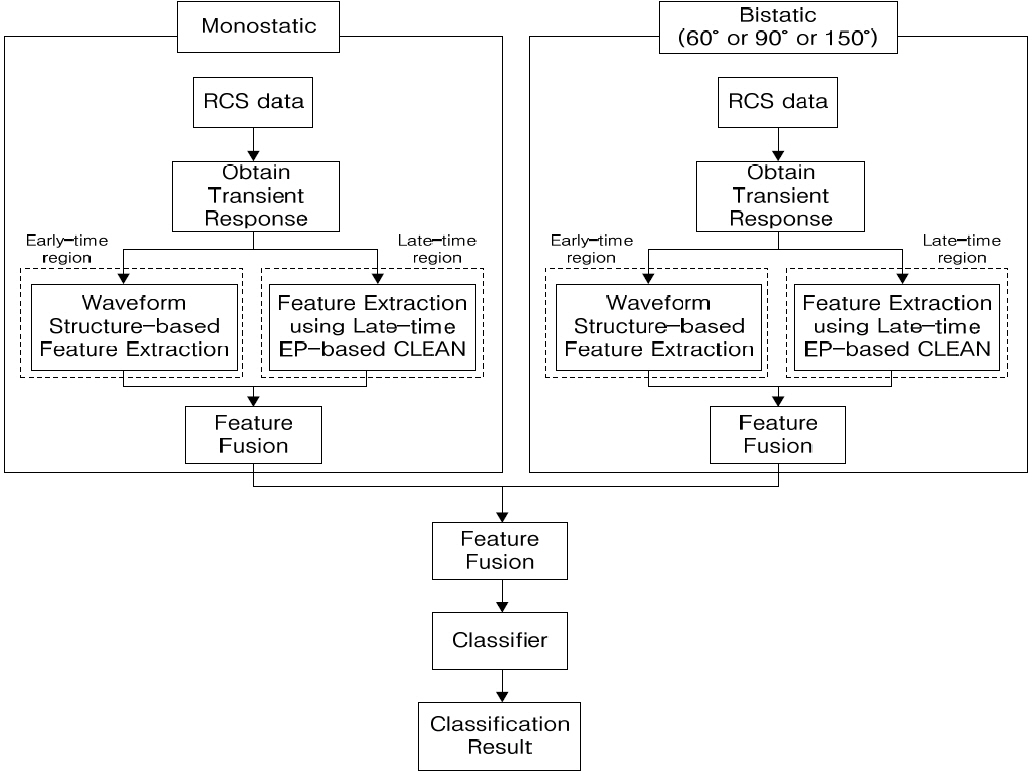
The proposed two-level feature vector fusion method can consider monostatic and bistatic structures, and use the feature vectors of both the early-time and late-time regions. Simulations were performed at several bistatic angles. Fig. 2 shows a block diagram of the proposed method.
V. Simulation and Results
First, we used FEKO, a widely used electromagnetic analysis tool, for the target classification experiment. RCS was obtained for eight 3D full-scale targets (B-2, F-22, F-15, F-117, MIG-29, SU-27, J-20, T-50) similar to the actual size of target, and time-domain signals were obtained by inverse FFT. From these time-domain signals, feature vectors of the early-time and late-time regions were extracted. We used the method of moments (MoM) option for the calculation. The selected frequency range was the HF band (0.2–28 MHz), the frequency sampling point was 140 points with 0.2 MHz intervals, and the polarization was HH (horizontally transmitting, horizontally receiving) polarization. Elevation angles were fixed at 0°, assuming the target to be at a long distance, and the aspect angles were 0° to 180°, with 1° intervals, resulting in a total of 181 points. In addition, 50 Monte Carlo simulations were performed to increase the reliability of the experimental results.
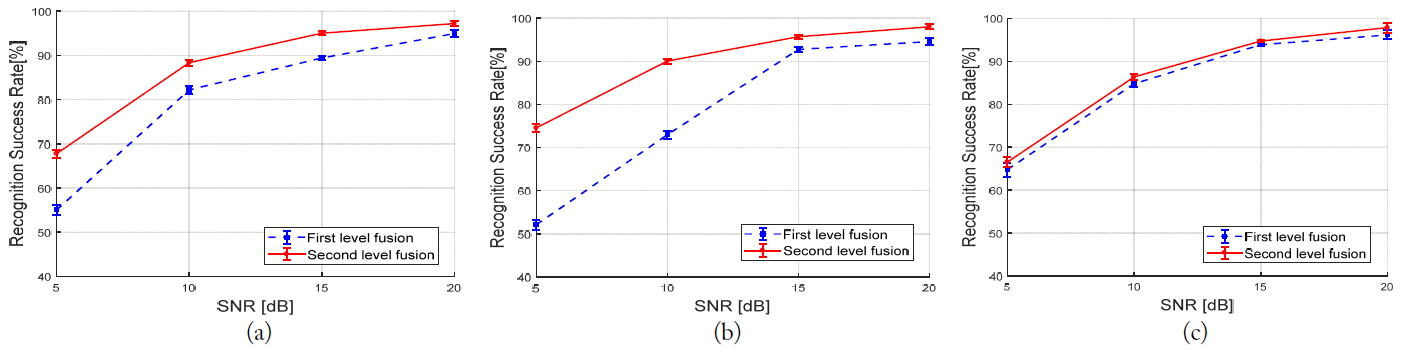
In the target classification experiment, a neural network classifier is trained until a mean square error of 10−3 was reached. Data with SNR = 20 dB were used as the training data, while white Gaussian noise was added to the test data, with SNR = 5, 10, 15, and 20 dB. We also compared the target classification performance at three bistatic angles of 60°, 90°, and 150° to find the best bistatic angle showing the best performance. Prior to the two-level feature vector fusion, the target classification experiment was performed through the one-level feature vector fusion which uses only the first-level fusion step. The target classification results using the 8-dimensional feature vectors obtained through the one-level feature vector fusion were compared with those using the 16-dimensional feature vectors obtained through the two-level feature vector fusion. Fig. 3 show the comparison of target classification performance for each bistatic angle. The target classification percentage is the average of 50 Monte Carlo simulations, and the standard deviation was also shown as bar.
As a result, at three bistatic angles of 60°, 90°, and 150°, target classification performance is improved when two-level feature vector fusion is used. At the bistatic angles of 60° and 90°, the lower SNR is, the more improved target classification performance is when the two-level feature vector fusion is used. At the bistatic angle of 150°, the difference between the one-level fusion and the two-level fusion is not big for all SNR.
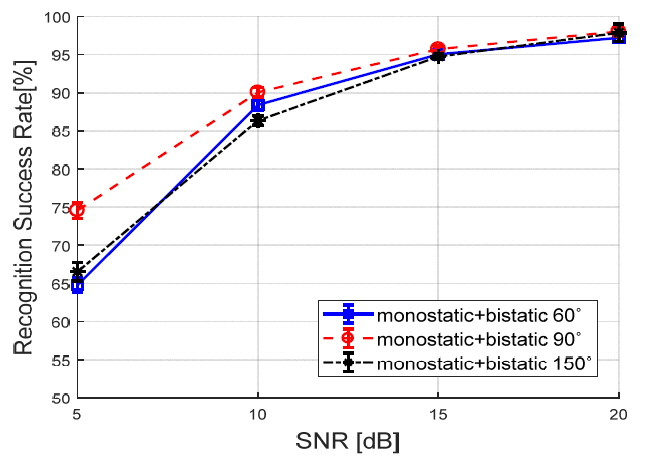
Fig. 4 compares the results obtained by combining monostatic structures at bistatic angles of 60°, 90°, and 150°. When the second-level feature vector fusion was performed at the bistatic angle of 90°, the best classification performance was obtained in all SNR environments. This means that the optimum selection of the second-level feature vector fusion is the monostatic and the bistatic of 90°. Also, in the low-SNR environment, there was a big difference in the target classification according to the bistatic angles, but there was not a big difference in the high SNR environment according to the bistatic angles.
As a result, both monostatic and bistatic radar structures were considered together with the feature vectors of both the early-time and late-time region. So, the target classification performance was improved by increasing the information of the target. Table 1 shows the confusion matrix at SNR = 20 dB and bistatic angle = 90°, which shows the best performance of the proposed method. The confusion matrix represents the relationship between the actual target and the classified target. The diagonal elements of the confusion matrix match the correct classification and other elements match the misclassification. In the confusion matrix shown in Table 1, the diagonal elements were close to 100% and the other elements of misclassification were very small. Therefore, we can overcome the problem of low resolution for the HF band radar by using the feature vector combining the resonance frequency and waveform structure.
VI. Conclusion
In this paper, we propose a two-level feature vector fusion method to improve the classification performance of the radar target. The proposed method combines the feature vectors of the early-time and late-time region and then combines them once more to the radar structure. We used the extracted parameters based on the waveform structure as the feature vector of the early-time region and the resonance frequency extracted by the late-time EP-based CLEAN algorithm as the feature vector of the late-time region. The feature vector based on the waveform structure and the resonance frequency can overcome the limitation of a narrow bandwidth in the HF band. To verify the performance improvement of the proposed method, we compared our method with the one-level feature vector fusion method, which fused only the feature vectors of the early-time region and the late-time region. The two-level fusion method is better than the one-level fusion method for all bistatic angles and all SNRs. We also do the simulation to find the optimum second-stage fusion combination for three bistatic angles. As a result, the best classification performance was obtained when the monostatic and bistatic 90° feature vectors were combined. Finally, we showed the confusion matrix of the proposed method. This result show that the all targets are well classified using the two-level feature vectors and misclassification is very small. Our method can be applied to the low frequency radar which can detect the low RCS targets such as stealth target or small missiles.