|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 18(4); 2018 > Article |
|
Abstract
An electromagnetic boundary-value problem of a tapered rectangular waveguide is rigorously solved based on eigenfunction expansion and the mode-matching method. Scattering parameters of the tapered rectangular waveguide are represented in a series form and calculated in terms of different rectangular waveguide combinations. Computation is performed to analyze reflection and transmission characteristics. Conductor loss by surface current density is also calculated and discussed.
Electromagnetic scattering from waveguide transition structures is a canonical problem. During the last few decades, there have been extensive studies on the scattering of waveguide transitions for many applications such as transformers [1], filters [2], and power dividers [3]. Moreover, a tapered waveguide can be used in a measurement system to characterize the electromagnetic properties of biaxial anisotropic materials [4].
The numerical method can be used to analyze electromagnetic scatterings from discontinuities in rectangular waveguides, but the more powerful method is the mode-matching method because it provides rigorous mode solutions in given regions. The analysis of the waveguide with one or more discontinuities is usually conducted using the mode-matching method in conjunction with the generalized scattering matrix technique [5–7]. In fact, the tapered structure can be analyzed using the mode-matching method by dividing the transition region into a number of sub-regions where the electromagnetic field can be defined in a series form of modes [2, 8, 9]. One study analyzed the rectangular waveguide transition using mode matching in X- to Ku-band applications to predict scattering parameters [2]. Studies on tapered waveguides have also been conducted using impedances [10], equivalent circuits, and the numerical method [11]. However, there has been no study on tapered waveguides based on the mode-matching method for V to W band applications, and much of the research has focused only on reflection and transmission characteristics to design the transition structure.
In this paper, we solve an electromagnetic boundary-value problem on a linearly tapered waveguide based on the mode-matching method. The eigenfunction expansion is used to represent the electromagnetic field in each region. The boundary conditions are enforced to obtain a set of simultaneous equations. Scattering parameters are represented in a series form and computed. To validate our formulation, simulation results of ANSYS High Frequency Structure Simulator (HFSS), a full-wave electromagnetic simulator, are compared with our results. Conduction loss in each rectangular waveguide is also calculated and discussed.
The geometry of a tapered rectangular waveguide is shown in Fig. 1. An incident wave is assumed to be TE10 mode, which is a dominant mode of rectangular waveguides. Region II should be divided into a number of rectangular waveguides to solve a boundary-value problem of a rectangular waveguide transition based on the mode-matching method. Each step waveguide has different widths and heights. A time convention of ejωt is suppressed throughout the analysis. The permittivities and permeabilities in each region are ε1, μ1, ε2, μ2, ε3, and μ3. In Region I, the incident and reflected fields based on vector potentials are:
where
k m n I = k 1 2 - ( m π a ) 2 - ( n π b ) 2 k 1 = ω μ 1 ɛ 1
where
k s i p i I I - ( i ) = k 2 2 - ( s i π x i ) 2 - ( p i π y i ) 2 k 2 = ω μ 2 ɛ 2
where
k u v I I I = k 3 2 - ( u π c ) 2 - ( v π d ) 2 k 3 = ω μ 3 ɛ 3 A m n - , B m n - , C s i p i + , C s i p i - , D s i p i + , D s i p i - , E u v + F u v +
In order to predict the transmission characteristics of the linearly tapered rectangular transition structure, we calculate scattering parameters that can be represented as:
With calculated modal coefficients, the incident and reflected powers in Region I (Pin, Pref) and the transmitted power in Region III (Ptrans) can be obtained as follows:
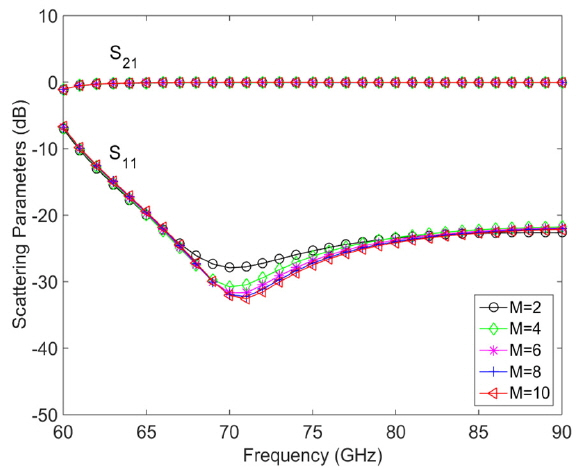
To validate our formulation and analyze the transmission characteristic of the tapered rectangular waveguide shown in Fig. 1, our computation results are compared with the simulation results from ANSYS HFSS. We take into account different combinations of rectangular waveguides designed for the V, E, and W bands in the analysis. The rectangular waveguides operating at each band have the following dimensions: aV = 3.7592 mm, bV = 1.8796 mm, aE = 3.0988 mm, bE = 1.5494 mm, aW = 2.54 mm, bW = 1.27 mm. Subscript represents the frequency band name at which rectangular waveguides operate. The tapered rectangular waveguide is assumed to have a linearly changing transition in Region II, and the length is L2 = 1 mm. Before dividing the transition region (Region II) into sub-waveguides, we check the convergence of our formulation. Fig. 2 illustrates scattering parameters against frequency in the case of V to W transition. Regarding S21, the results show sufficient convergence. Likewise, S11 results also converge. Therefore, the transition region is divided by 10 rectangular waveguides (M = 10). The number of modes used in our computation is N = 6 to achieve convergence to within 0.5 dB. These numbers of modes are used throughout the analysis unless specified. Fig. 3 shows a simulation model of the linearly tapered rectangular waveguide in ANSYS HFSS and illustrates the comparison of computed scattering parameters based on our formulation with those of the HFSS simulation. The comparison between our results and the simulation results shows good agreement. From the results, it is verified that our formulation based on the mode-matching method is valid. Cut-off frequencies of rectangular waveguides operating at the V, E, and W bands are 39.9, 48.4, and 59 GHz, respectively. Therefore, the reflection of V to W (Fig. 3(b)) or E to W (Fig. 3(c)) near 60 GHz is larger than the reflection of the V to E (Fig. 3(d)) transition.
In order to check that the dominant mode is sustained through the transition structure, the electric field distribution and surface current density in a receiving waveguide (Region III) are plotted in Fig. 4 in a case of V to W transition at 75 GHz. The electric field distribution is calculated at the center of the waveguide parallel to the wider plane and all truncated modes are considered. The electric field distribution is similar to that of TE10. Moreover, the surface current density on the inner walls is similar to that of TE10. In addition, higher modes contribute to purely reactive powers and are evanescent modes produced by the junctions. The mode-matching method can provide the physical meaning, including the effects of each mode on the scattering characteristics, if the higher propagating modes exist in structures such as the W to V junction. As a result, the tapered rectangular waveguide with a linearly changing slope can transmit most of the incident energy to the receiving port without a significant change of mode.
Because of the existence of surface current densities on the inner walls of the rectangular waveguide, conductor losses must exist. Conductor loss is defined as in [13]:
where
R s = ω μ / 2 σ
Total length is 3 mm, and the length of the waveguide for V band is 1 mm in the transition structure.
We have solved the electromagnetic boundary-value problem of the tapered rectangular waveguide based on eigenfunction expansion and the mode-matching method. Scattering parameters are represented in a series form and computed under different combinations of rectangular waveguides operating at the V, E, and W bands. Our formulation can also be applied to various transition structures and can be used researching a measurement system using waveguide transition structures.
Acknowledgments
This research was supported by Physical Metrology for National Strategic Needs funded by Korea Research Institute of Standards and Science (No. KRISS-2018-GP2018-0005).
Fig. 3
(a) Simulation model of the tapered rectangular waveguide in ANSYS HFSS and a comparison of our computation results with the HFSS simulation results. (b) V to W, (c) E to W, and (d) V to E transitions.
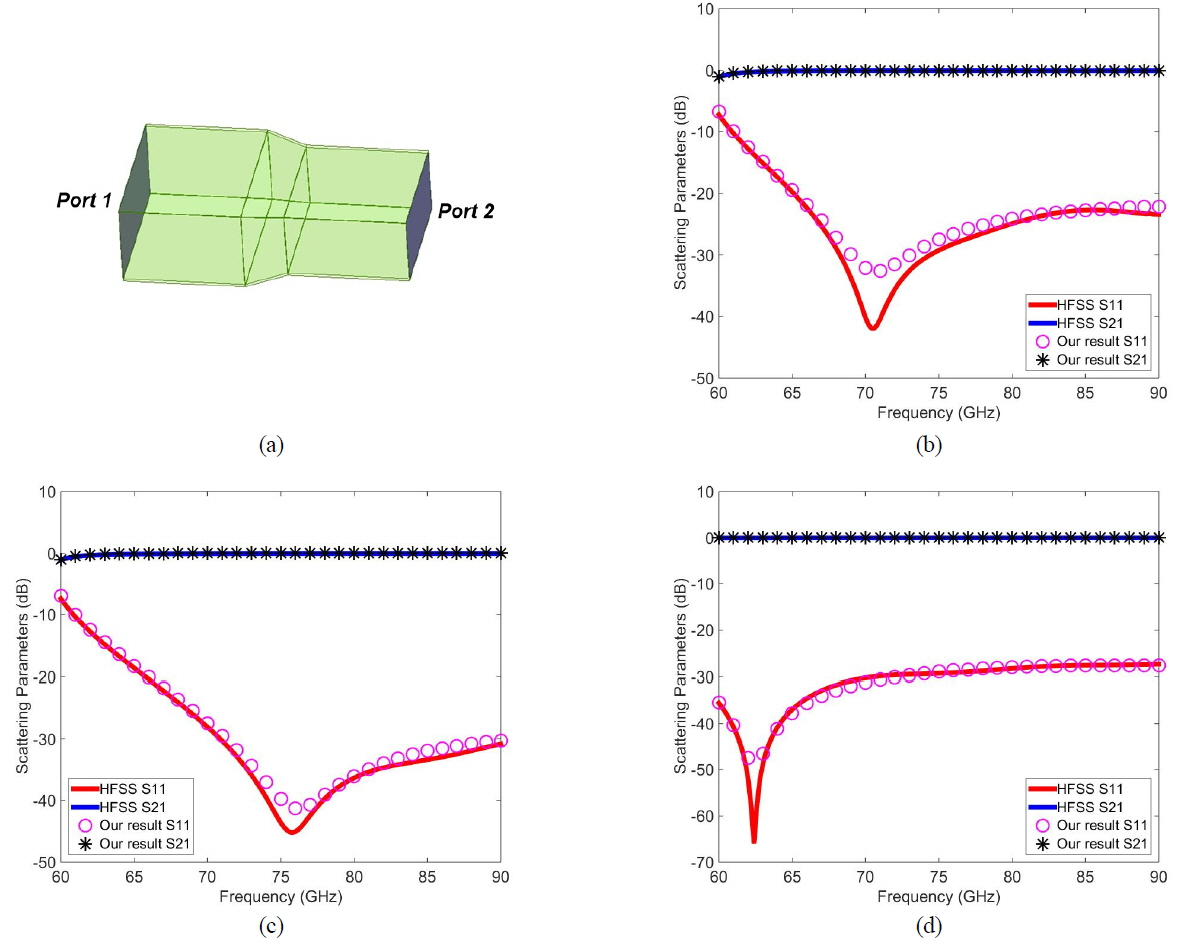
Fig. 4
(a) Electric field distribution at the center of the receiving waveguide and (b) side view and (c) top view of surface current density on the walls of the receiving waveguide.
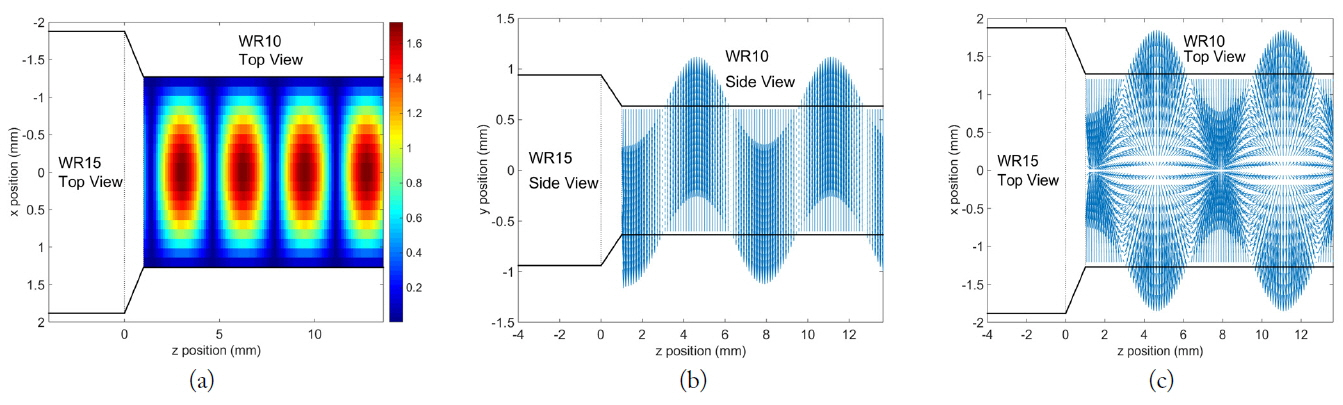
Table 1
Conductor loss of the general rectangular waveguide (WR15) and the single step and tapered transition structure (V to W)
| Conductor loss (%) | |
|---|---|
| WR15 (no transition) | 0.0917 |
| Single step transition | 0.1868 |
| Tapered transition (Fig. 4) | 0.1559 |
References
1. J Bornemann and F Arndt, "Modal-s-matrix design of optimum stepped ridged and finned waveguide transformers," IEEE Transactions on Microwave Theory and Techniques, vol. 35, no. 6, pp. 561–567, 1987.

2. H Patzelt and F Arndt, "Double-plane steps in rectangular waveguides and their application for transformers, irises, and filters," IEEE Transactions on Microwave Theory and Techniques, vol. 30, no. 5, pp. 771–776, 1982.

3. F Arndt, I Ahrens, U Papziner, U Wiechmann, and R Wilkeit, "Optimized E-plane T-junction series power dividers," IEEE Transactions on Microwave Theory and Techniques, vol. 35, no. 11, pp. 1052–1059, 1987.

4. A Knisely, M Havrilla, and P Collins, "Biaxial anisotropic sample design and rectangular to square waveguide material characterization system," In: Proceedings of 2015 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (Metamaterials); Oxford, UK. 2015, pp 346–348.

5. L Christie and P Mondal, "Mode matching method for the analysis of cascaded discontinuities in a rectangular waveguide," Procedia Computer Science, vol. 93, pp. 251–258, 2016.

6. T Shibata and T Itoh, "Generalized-scattering-matrix modeling of waveguide circuits using FDTD field simulations," IEEE Transactions on Microwave Theory and Techniques, vol. 46, no. 11, pp. 1742–1751, 1998.

7. JA Torres and JJ Saenz, "Improved generalized scattering matrix method: conduction through ballistic nanowires," Journal of the Physical Society of Japan, vol. 73, no. 8, pp. 2182–2193, 2004.

8. T Wriedt, KH Wolff, F Arndt, and U Tucholke, "Rigorous hybrid field theoretic design of stepped rectangular waveguide mode converters including the horn transitions into half-space," IEEE Transactions on Antennas and Propagation, vol. 37, no. 6, pp. 780–790, 1989.

9. YB Park, KC Hwang, and I Park, "Mode matching analysis of a tapered coaxial tip in a parallel-plate waveguide," IEEE Microwave and Wireless Components Letters, vol. 18, no. 3, pp. 152–154, 2008.

10. RC Johnson, "Design of linear double tapers in rectangular waveguides," IRE Transactions on Microwave Theory and Techniques, vol. 7, no. 3, pp. 374–378, 1959.

11. S Dwari, A Chakraborty, and S Sanyal, "Analysis of linear tapered waveguide by two approaches," Progress In Electromagnetics Research, vol. 64, pp. 219–238, 2006.

12. CA Balanis, Advanced Engineering Electromagnetics. New York, NY: John Wiley & Sons Inc, 2012.
13. DM Pozar, Microwave Engineering. New York, NY: John Wiley & Sons Inc, 2011.
Biography
Sangsu Lee received a BS degree from the Department of Electrical and Computer Engineering at Ajou University, Suwon, Korea in 2017. He is currently working towards an M.S. in Department of Electrical and Computer Engineering, Ajou University, Suwon, Korea. His research interests include electromagnetic field scattering analysis and metamaterials.

Biography
Jae-Yong Kwon received a B.S. degree in Electronics from Kyungpook National University, Daegu in 1995 and M.S. and Ph.D. degrees in Electrical Engineering from the Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea in 1998 and 2002, respectively. In 2001, he was a Visiting Scientist at the Department of High-Frequency and Semiconductor System Technologies, Technical University of Berlin, Berlin, Germany. From 2002 to 2005, he was a Senior Research Engineer at the Devices and Materials Laboratory, LG Electronics Institute of Technology, Seoul, South Korea. Since 2005, he has been a Principal Research Scientist with the Division of Physical Metrology, Center for Electromagnetic Metrology, Korea Research Institute of Standards and Science, Daejeon. Since 2013, he has been a Professor of the Science of Measurement at the University of Science and Technology, Daejeon. His current research interests include electromagnetic power, impedance, and antenna measurement. He is an IEEE Senior Member.

Biography
Dongchan Son received a B.S. degree from the Department of Electrical and Computer Engineering at Ajou University, Suwon, Korea in 2017. He is currently working towards an M.S. in the Department of Electrical and Computer Engineering, Ajou University, Suwon, Korea. His research interests include electromagnetic field scattering analysis and frequency selective surfaces.

Biography
Yong Bae Park received B.S., M.S., and Ph.D. degrees in Electrical Engineering from the Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea, in 1998, 2000, and 2003, respectively. From 2003 to 2006, he was with the Korea Telecom Laboratory, Seoul, Korea. In 2006, he joined the School of Electrical and Computer Engineering, Ajou University, Suwon, Korea, where he is now a Professor. His research interests are electromagnetic field analysis and electromagnetic interference and compatibility.

- TOOLS
- Related articles in JEES
-
The Design of a Sliding Rectangular Waveguide Array Antenna for Beam Steering2023 May;23(3)