Health Effects Study and Safe Distance Determination Near an Electrical Distribution Network
Article information
Abstract
Living organisms are affected by environmental pollution, one main source of which is the electric and magnetic fields (EMFs) of electrical distribution lines that produce high-voltage currents. Nowadays, electrical power transmission lines and distribution systems are becoming increasingly prevalent, with power distribution lines passing through cities and being located very close to buildings. For this reason, there has been significant public concern, which has escalated because of reports about the adverse health effects of the EMFs of power distribution systems. In this paper, the environmental pollution produced by several different configurations of electrical distribution systems in Iran is studied. The paper presents new software to calculate EMFs around electric power lines. Using this software and based on maximum allowable EMFs, a safe margin around selected power lines has been determined. According to the study results, it seems that in Iran this safe distance is not met. Therefore, the standards relating to power distribution lines should be reviewed.
I. Introduction
Previous studies on the effect of the electric and magnetic fields (EMFs) of power lines on health have produced inconsistent and often contradictory results [1]. Many people are concerned about power frequency (50 Hz) EMFs produced by electrical distribution lines (EDLs) because the research indicates possible harmful effects of exposure to these fields. According to previous studies and electromagnetic fields standards, the maximum allowable magnetic field is 0.04 μT, and the maximum allowable electric field is 4–5 kV/m [1, 2]. Many studies have addressed the evaluation of the electrically induced voltage and current in living organisms [1, 2]. The conclusion is that power lines are generally assumed to be harmless. However, this assumption has never been adequately tested. Low-level harmful effects could be missed, even though they might be an important issue for the population as a whole, particularly as electric lines are ubiquitous. Other studies have evaluated the EMFs of different power lines that are considered major sources of pollution [3–9]. These fields may affect the operation of nearby electric and electronic devices and appliances and may affect various living organisms [1–5]. Electric distribution systems are becoming increasingly prevalent worldwide, but despite this the environmental effects of EMFs have not been adequately studied. In recent years, there has been significant public concern prompted by reports on the adverse health effects of EMFs [6]. As stated, existing studies on the environmental pollution of EMFs [1–9] report the maximum allowable electric field to be 4–5 kV/m and the maximum allowable magnetic field to be 0.04 μT for small animals and about 4–100 μT for humans, depending on body area and the value of the line voltage and current [1, 2]. Unfortunately, in Iran power lines in cities have been developed irregularly and are very close to the place of human life. In this paper, we have developed a new software package using MATLAB to calculate EMFs around electrical lines. By analyzing the results, the environmental pollution level around electrical distribution systems (EDSs) can be determined and the safe distance calculated.
II. Electromagnetic Fields
Electric fields are created only when there is electric voltage. The magnitude of an electric field is proportional to the voltage of an electric line. There is no relationship between electric field strength and current. In the literature, electric field data are presented in units of V/m. Electric fields are caused by electric charges and are described by Gauss’s law. This is used to find the electric field generated by voltage in highly symmetric geometries, such as an infinitely long wire. Gauss’s law may be expressed as:
where Q is the electric flux through a closed surface S, E is the electric field,
where the line integral is over any arbitrary loop, I is the current enclosed by that loop, and r is the distance from the center of the wire. Using Ampere’s Law, the magnetic fields of power transmission lines can be calculated [1].
III. History of the Health Effects of EMFs
After more than three decades of research, there is still public concern regarding exposure to EMFs and the increased risk of childhood cancer. This concern largely derives from studies of people living near power lines or working in electrical-related occupations. Some of these studies appear to show a weak association between exposure and power-frequency EMFs and the incidence of some cancers. Concerns about the EMFs of power lines were first raised in a 1979 study that associated an increased risk of childhood leukemia with residential proximity to power lines [2]. In 1998, an international panel of experts convened by the National Institute of Environmental Health Sciences reported that EMFs like those surrounding electric power lines should be regarded as a possible human carcinogen [1–3]. Some diseases reportedly caused by electromagnetic radiation include childhood leukemia, brain tumors, and neurodegenerative diseases, such as Alzheimer disease. Health risks from high-voltage power lines are not limited to children, and a study published in 2008 reported an increase in the incidence of Alzheimer disease in a population living near high-voltage power lines [3]. Recent laboratory studies suggest that EMFs with intermittent or transient characteristics may produce biological effects [4]. Many studies [1–7] have attempted to determine whether childhood cancer can be linked to magnetic fields from power lines. Different confounding factors, such as air pollution, water contamination, exposure to hazardous chemicals, heavy traffic, and housing density, could conceivably contribute to cancer. Experimental studies [10–14] conducted on more than 2,500 animals of different species (mice, cats, rabbits, and monkeys) have aimed to evaluate the most sensitivities, body nervous and immune systems, and also vital activity. The results of this research confirm a relatively biological activity of 50 Hz magnetic fields. It was concluded that the biological effects of 50 Hz magnetic fields depend on the exposure intensity and duration. The obtained data on changes in the immune and other systems indicated that a value of 0.04 μT magnetic flux density during 4 hours per day of exposure had adverse health effects on the experimental animals. This value is higher for humans and depends on body area and the value of the line current. All these studies clearly reveal that the health risks associated with high-voltage power lines and can affect a significant amount of people living in proximity to these lines.
IV. Software Package
MATLAB is one of the most powerful engineering applications. In this work, we used MATLAB to develop a program to calculate the EMFs around transmission lines in three-phase systems. The input parameters included the voltage of wires, the current, the height of transmission towers, the diameter of wires, and the position of the phases. By using input data and based on the equations in Section II, EMFs around distribution systems at a constant height from the ground or in a fixed width of the transmission tower can be calculated. The main menu of the developed software is shown in Fig. 1.
V. Calculation of EMFs around Electrical Distribution Lines
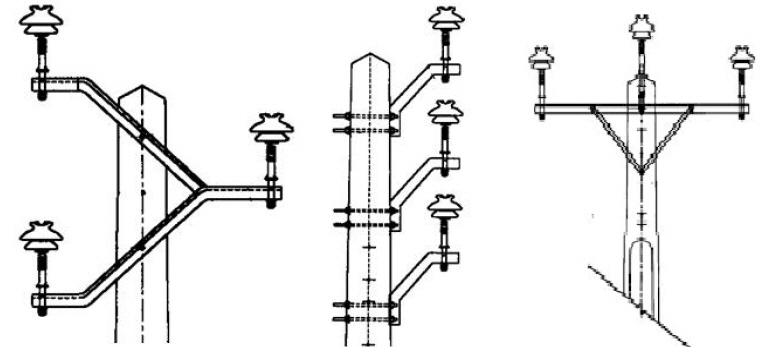
In Iran, several line configurations are installed for different distribution voltage levels. Fig. 2 shows several typical lattice-type configurations for the 20 kV level.
The data for these cases are listed in Table 1.
Fig. 3 shows the most common configurations for 400 V lines.
The data for these cases are listed in Table 2.
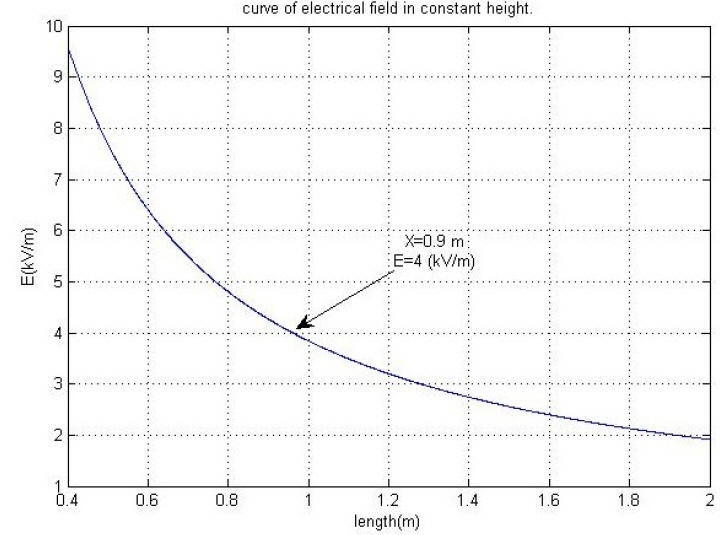
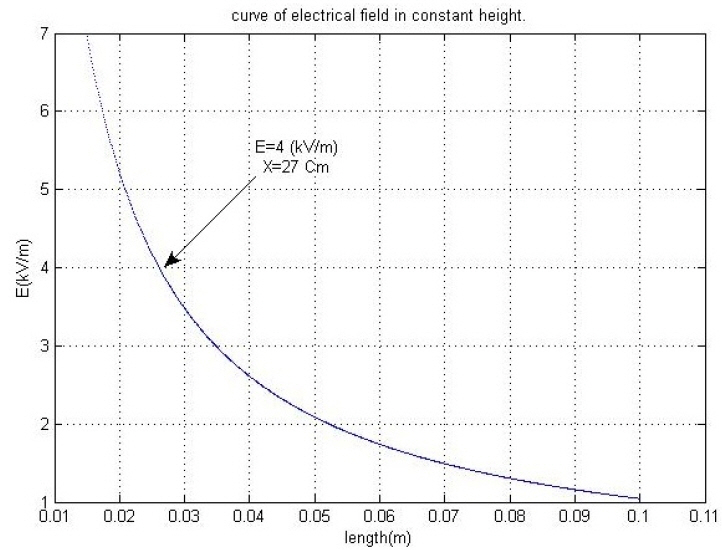
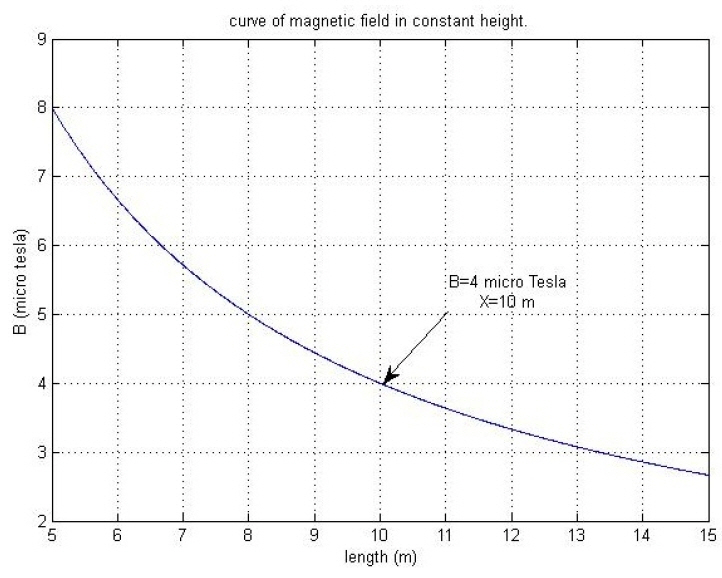
VI. Results and Safe Margin Calculation
According the previous studies that mentioned above, maximum allowable electric fields is 4–5 kV/m and maximum allowable magnetic field is 0.04 μT for small animals and about 4–100 μT for humans, and it will depend on the percentage area of the human body with respect to the animal’s body area and also on the value of the line voltage and current. The results of this study are listed in Table 3.
Based on these results, it can be concluded that:
Environmental pollution in the form of electric fields is minimal and can be contained; therefore, the health effects relating to electric fields are negligible.
The magnetic fields of EDLs are a form of environmental pollution, and based on previous studies, living near power lines can be detrimental to human health.
Environmental pollution in the form of magnetic fields is much greater than environmental pollution in the form of electric fields and should be studied carefully.
Living close to EDLs may be hazardous.
Based on electric distribution design standards in Iran, there must be a minimum horizontal distance of 3 m between any part of a building and the closest 20 kV line and 1.5 m between any part of a building and the closest 400 V line. It seems that the safe distance standards for power distribution lines should be reviewed.
VII. Conclusion
This paper investigated environmental pollution caused by EMFs near EDSs in Iran. A software package was developed using MATLAB to calculate these EMFs. Using this software, EMFs near 20 kV and 400 V distribution lines were determined. Based on the results and on safe EMF levels, safety margins around EDLs were calculated. It was shown that environmental pollution in the form of electric fields is minimal, but environmental pollution in the form of magnetic fields is significant enough to warrant careful study. It seems that the safe distance standards for power distribution lines should be reviewed.
References
Biography
Mehdi Nafar received his B.S., M.S., and Ph.D. degrees in electrical engineering in 2002, 2004, and 2011 from PWIT University, Amirkabir University of Technology, and Islamic Azad University, Science and Research Branch, all in Tehran. He graduated from all programs with First Class Honors. He is currently Assistant Professor in the Department of Electrical Engineering, Marvdasht Branch, Islamic Azad University in Marvdasht, Iran. He is the author of more than 50 journal and conference papers. His teaching and research interests include power system and transformer transients, lightening protection, and optimization methods in power systems.