I. Introduction
Synthetic aperture radar (SAR) imaging technology is one of the most promising technologies utilized in various observation areas such as terrain, resource, and target searches. With the increasing demand for imaging technology, SAR systems have been developed to achieve high resolution and wide swath for accurate target detection, regardless of weather or environmental changes. To obtain high-resolution images, the SAR system can be improved in two ways. The first is a budget parameter optimization of the transmission and reception systems to reduce the ambiguity of radar signals and various interference problems. The second is to use diverse SAR signal processing algorithms for high-resolution image extraction. However, considering the cost and physical volume of the SAR system, an effective way to obtain high-resolution images is with diverse signal processing techniques.
There are numerous signal processing algorithms such as the range Doppler algorithm (RDA), chirp scaling algorithm (CSA), omega-K algorithm (ω-k), back projection algorithm (BPA). The RDA is widely used for efficient and stable signal processing because it is simple and easy to use. However, when the RDA is used for image processing, the final image is not focused due to random environmental variables. To cope with environmental variables and acquire high-resolution images, precise estimations of the Doppler centroid frequency and chirp rate are required in the algorithm. Many researchers have proposed algorithms to correct the received signal by removing the unexpected signals, using the magnitude or phase information of the chirp signal based on average cross-correlation coefficient (ACCC), multi-look cross correlation (MLCC), and multi-look beat frequency (MLBF) methods [1, 2]. However, the Doppler parameters extracted through previous algorithms still have uncertainty because of topographic change of interest area and interference of unexpected signal. Therefore, many researchers have attempted to increase the accuracy of Doppler parameters in various SAR experiments [3–6]. This paper proposes a novel method to solve the uncertainty by considering uncorrected Doppler parameters. In conventional SAR experiments, signal processing was performed by estimating the constant velocity with the lowest ambiguity error. This conventional method can obtain a reasonable image quality over the entire area if the area of interest has a nearly constant height over whole region. However, if the difference of altitude in the area and the direction of measurement is changeable, a high-quality SAR image cannot be obtained with only a constant velocity. Based on the changes of velocity in the area of interest, the quality of a SAR image can be improved using cross-correlation theory, designed for SAR. The estimated velocity is used to acquire a high resolution SAR image without complicated processing techniques. To evaluate the proposed method, the raw data obtained from practical experiments are used. Finally, high-resolution SAR images are constructed, applying the proposed algorithm to various environmental changes of automobile-based SAR (Auto-SAR).
II. SAR Signal Processing Analysis of the RDA
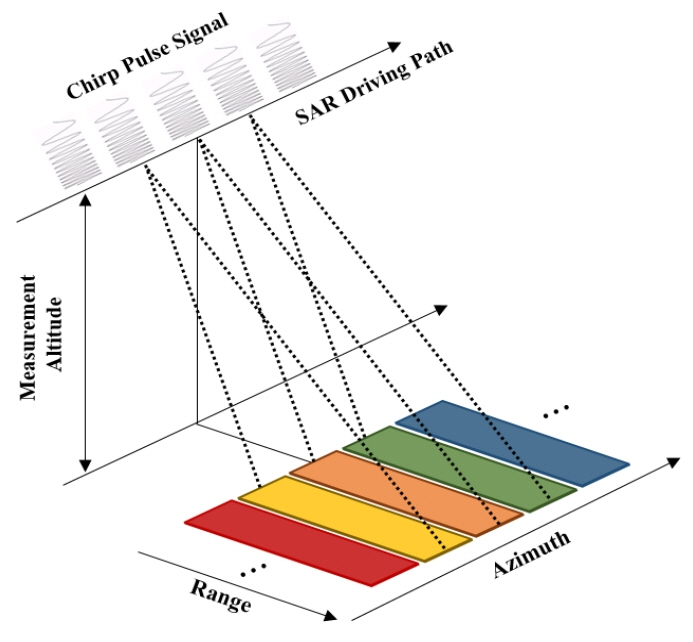
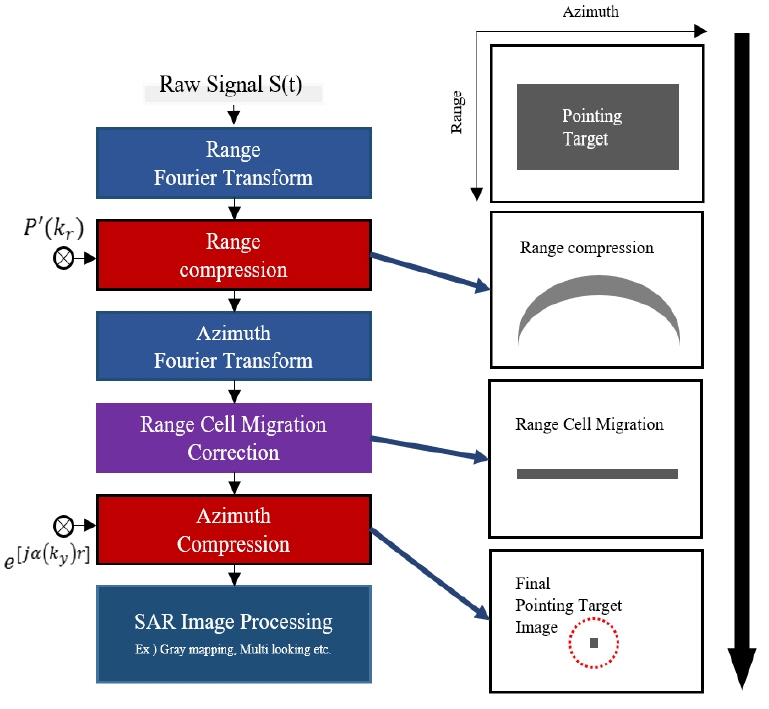
The RDA is a method of compressing raw data using a matched filter in the range direction and azimuth direction, respectively. As shown in Fig. 1, the RDA is typically used in stripmap standard mode with chirp pulse signals. The basic signal processing procedure consists of range and azimuth compressions and range cell migration, as shown in Fig. 2. Doppler centroid estimation can be applied to obtain high-resolution images in the SAR ground experiment. In case of the ground experiment, the image difference caused by the Doppler centroid variation is insignificant [1]. Therefore, it is possible to exclude the Doppler centroid estimation in a mathematical mechanism for SAR signal processing. The chirp pulse signals in the range and azimuth directions received from the SAR system are as follows, respectively.
τ and η are the time, ω
r
and ω
a
are the window functions each chirp pulse signal, A
r
and A
a
are the amplitude constant values, f
0 and f
η
c
are the center frequency of chip pulse signal, and K
r
and K
a
are the chirp rate of the signals. The first and second parameters mentioned above are for the range and azimuth direction, respectively. R(η) in (1) is the instantaneous slant range. Eqs. (1) and (2) are approximated as (3) through the range and azimuth compressions and range cell migration. After the range cell migration of SAR data, the performance of resolution for the matched filter in the azimuth direction can be determined according to K
a
and f
η
c
. The final SAR image signal, S
final
(τ,η), is as follows.
Therefore, it is more important to estimate the exact matched filter in the azimuth direction than the range direction because the errors of K
a
and f
η
c
are vulnerable by the SAR measurement environment, such as the actual speed, changing rate in the distance to the target, and motion vibrating conditions. However, the matched filter in the range direction has a low error rate because the raw data are compressed using the system parameters or loop-back chirp pulse signal. Therefore, our proposed algorithm estimates the accurate velocity in each range, which is an important parameter for the azimuth matched filter.
III. Proposed SAR Processing Algorithm
Based on the RDA, the modified signal process of the Doppler parameter is proposed in this section. To estimate the azimuth matched filter that fits with the actual signal, the exact Doppler centroid, f
η
c
(τ) and Doppler chirp rate, K
a
(τ) are required under variable terrain conditions [7–9]. The Doppler parameters are as follows.
θ
s
is the squint angle for measuring the target, λ is the wavelength of the center frequency in the chirp pulse signal, and R
0(τ) is the slant range along to the range time. The Doppler parameters are addressed as a function of the vehicle velocity, V
s
. Therefore, the main reason for the uncorrected azimuth matched filter is the misestimated velocity. This velocity leads to the low quality of the SAR image. The velocity estimation of each range can lead to more the high-resolution quality and precise target classification than the conventional results of the SAR processing. To find the accurate velocity V
s
, the proposed algorithm incorporates cross-correlation technique into the estimation of the Doppler parameter [10, 11]. If S(τ,η) is a 2D signal constructed in the range and azimuth, the cross-correlation function is defined as follows.
τ
n
is the slow time and, η is the fast time. Based on (6), the chirp pulse frequency of the range-Doppler domain along the range is divided into two looks (Look1, Look2), having V
s
+ ΔV
error
in phase information. A matched filter of assumed V
s
multiplies each look, and then inverse.
FFT is used to generate the images of each look with a phase error. The cross-correlation values between two images are compared until reaching the smallest correlation value, changing V
s
. Range cell migration correction (RCMC) and azimuth compression are performed, using the V
s
defined from finishing the cross-correlation estimation in each range cell with phase variance compensation. In the conventional SAR process, each step of RDA uses its own technology to compensate the phase error for every range cell. It is time-consuming and complicated, resulting in low efficiency. However, in the proposed technique, all steps are performed at once without any other process using the estimated V
s
. Unlike airborne- and spaceborne-SAR, which are sensitive to environmental changes, the proposed algorithm is suitable for Auto-SAR to make real-time processing fast and easy, resulting in high efficiency.
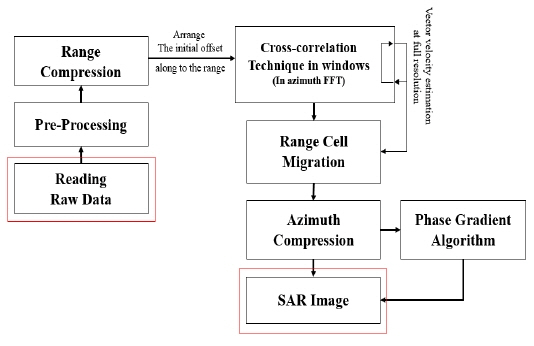
From the estimated results, the defined V
s
can vary over a range, such as a vector. Therefore, the V
s
is defined as the vector velocity. The most suitable V
s
depends on the direction of the target. Before the practical experiment, impulse response function (IRF) analyses using the proposed algorithm are performed in Fig. 3. Fig. 3(a) and (b) show the analysis structure in 2D and the Doppler chip pulse signal according to the range, respectively. Fig. 3(c) shows that estimating the correct V
s
improves the peak value and the 3-dB resolution of IRF of the target in the SAR image. Fig. 4 shows over whole signal processing of the proposed algorithm by organizing the process described in this section.
IV. Experiment Results and Performance
To evaluate the performance of the proposed algorithm, the X-band SAR system was implemented and the practical experiment was conducted. Table 1 shows the specifications of the X-band SAR system.
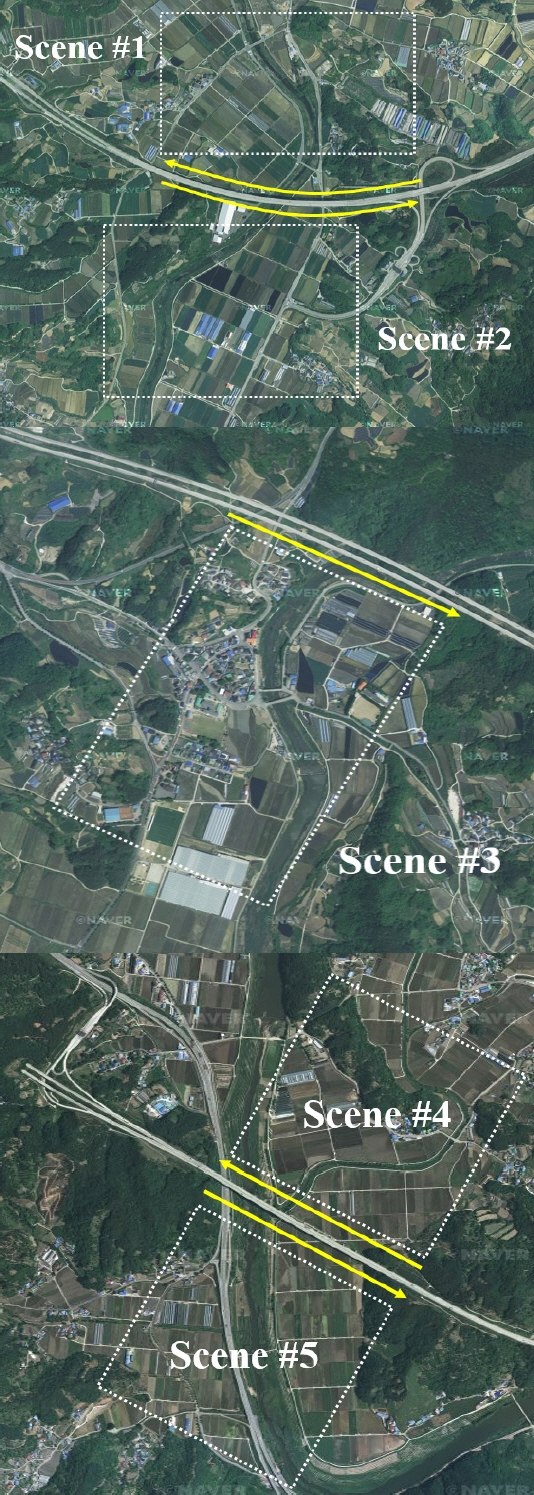
As shown in Fig. 5, two antennas are installed as the transmitter and receiver, respectively. The stop-and-go method is applied to measure the practical SAR experiment. To prove the validity of the proposed SAR algorithm, five different regions are selected. In particular, two curved terrains are included in the practical experiment regions. Fig. 6 shows the practical measurement locations, which are taken while driving through an express highway. Scenes #1 and #2 are places to drive through curved loads, Scene #3 is a lower elevation terraced region as the range increases along the distance. Scenes #4 and #5 are rice fields measured in both directions at a height of 60 m. Applying vector velocity estimation, the quality of the SAR image is significantly improved over conventional RDA in all regions, as shown in Fig. 7. Fig. 8 shows the difference before and after applying the vector velocity to Scenes #1 and #2, respectively. As shown in the images in Fig. 8, we can see the performance of the algorithm through the focusing improvement in practical experiments. In addition, as confirmed in Figs. 7 and 8, the proposed technique can be applied to various terrain and experimental conditions in Auto-SAR. In Fig. 9, analysis of the corner reflector in Scene #5 shows that the vector estimation improves the 3-dB resolution of the IRF and increases the peak energy of the main lobe. Through the estimated velocity is closer to the accurate velocity, the energy balance of the sinc-function is addressed more clearly. These results suggest that the desired resolution and high-quality SAR image can be obtained by the correction of the vector velocity.
V. Conclusion
The proposed algorithm is suitable for measuring the image in Auto-SAR. The recent technology has complex process to compensate for the phase error in each range cell for airborne-and spaceborne-SAR. It is inefficient in creating SAR images in Auto-SAR. However, the proposed technology is easy to handle and provides fast performance, allowing an immediate response to a variety of situations that can occur on the ground. Applying the precise estimation of the vector velocity can provide more accurate signal processing for high-quality SAR images. To prove the effectiveness of the proposed algorithm, high-quality results are acquired from practical experiments. In addition, the proposed technique of vector velocity is expected to be applied in various conditions, such as sub-aperture correction, spotlight mode, and autofocus.