Unequal Power Dividers Using Uniform Impedance Transmission Lines with Stubs

Young-Chul Yoon; Young Kim

doi:10.26866/jees.2021.21.1.44

Abstract

This study proposes an impedance control method in transmission lines using open- or short-circuit stubs for unequal power dividers. The proposed method is based on the conversion of a two-port to a three-port transmission line, which is equivalent to multiplying the impedance at the internal transmission line by a scaling factor and then connecting open- or short-circuit stubs in parallel to each port on the three-port transmission line. To verify the effectiveness of the proposed method, Wilkinson and Gysel power dividers with splitting ratios of 9:1 and 5:1, respectively, using uniform impedance transmission lines with open- or short-circuit stubs at an operating frequency of 2 GHz were designed. The experimental measurements of the two power dividers agree well with those of the simulation.

Keywords: Gysel Divider, Impedance Control Method, Open- or Short-Circuit Stub, Unequal Divider, Wilkinson Divider

I. Introduction

Power dividers are passive components essential for configuring wireless communication and equipment. Recently, many studies have been conducted regarding the application of asymmetric splitters to circuits with various uses, such as Doherty amplifiers [1] and antenna feeders [2]. Conventional asymmetric splitters have employed quarter-wavelength transmission lines of low and high impedances according to splitting ratios. However, the transmission line width of asymmetric splitters is either extremely large or extremely small to be implemented using microstrip technology.

To overcome implementation problems such as that of the planar structure microstrip, a thick material with a low dielectric constant [3–5], a suspended strip structure [6], or a defected ground structure (DGS) [7] can be used to realize a high-impedance transmission line. In addition, because low-impedance transmission lines have very large line widths, a structure with open-circuit stubs connected in parallel to the transmission line can be used to implement a suitable low-impedance transmission line [8]. However, the methods that use thick material or mechanical structures for low- or high-impedance transmission lines are applicable under limited conditions only.

In this study, to implement high- or low-impedance transmission lines, we propose an impedance control method for converting a two-port transmission line into a three-port transmission line. This method uses a three-port transmission line with an adjusted scaling factor that increases or decreases the internal impedance of the converted transmission line. In addition, it operates the equivalent circuit as one that connects open- or short-circuit stubs in parallel to each port on the three-port impedance line.

Using this method, an asymmetric power divider was designed by converting its low- and high-impedance transmission lines into suitable uniform impedance transmission lines that were connected in parallel to open- or short-circuit stubs. As an example, a 9:1 asymmetric Wilkinson power divider and a 5:1 Gysel power divider [9–11] were designed and measured at an operating frequency of 2 GHz.

II. Theory of Impedance Control Method

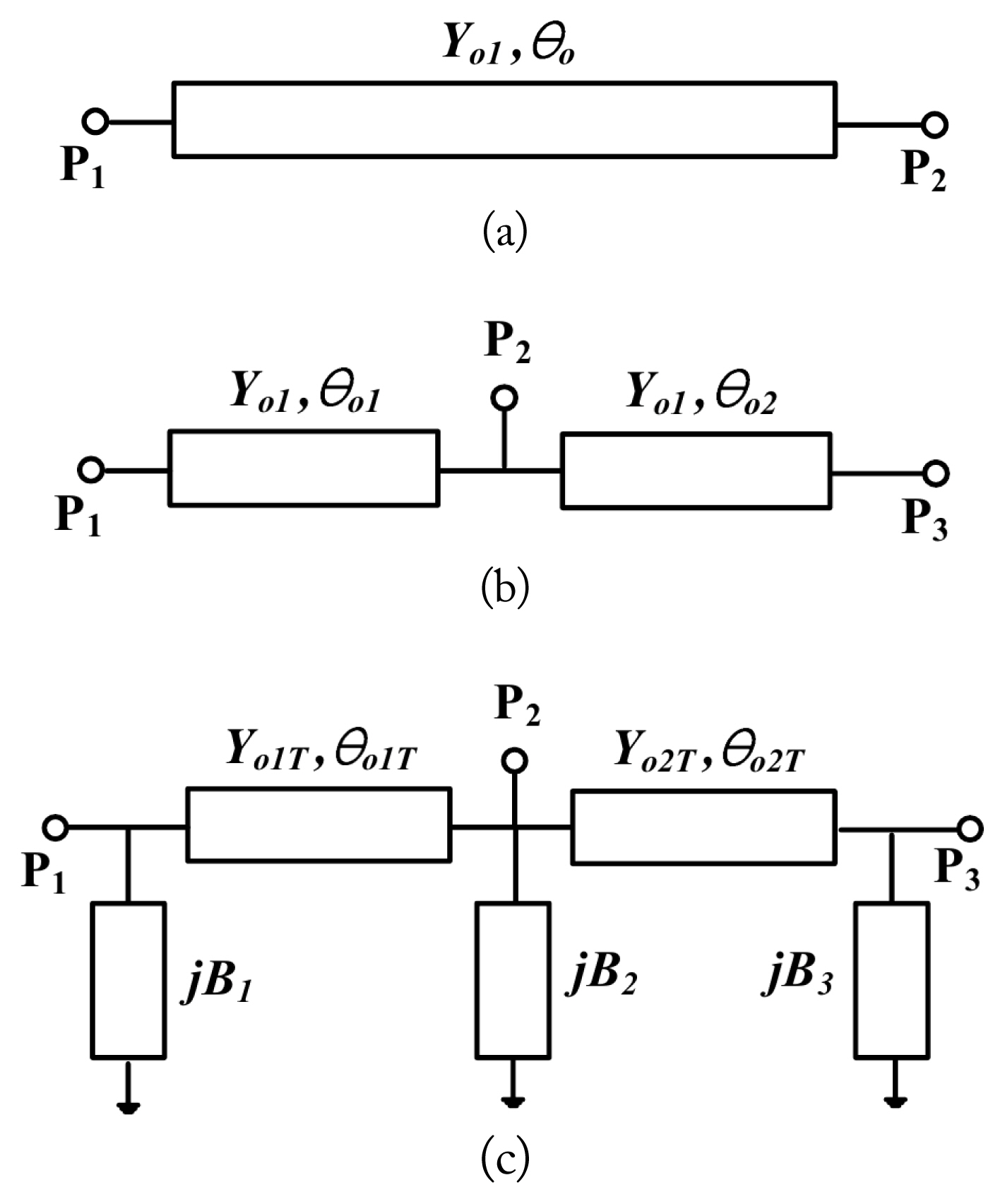
Fig. 1(a) depicts a transmission line with a characteristic admittance Y_o₁ and electrical length θ_o. This transmission line can be modified with port 2 inserted in the middle, as shown in Fig. 1(b) [12, 13]. The electrical length of the modified transmission line is

(1)

θo=θo1+θo2

In this case, the admittance parameters of the transmission line to which port 2 is added are

(2)

(Y)=jYo1(-cot θ01csc θ010csc θ01-cot θ01-cot θ02csc θ020csc θ02-cot θ02).

Without affecting the termination impedance of port 1 and 3, the internal impedance of port 2 can be adjusted by multiplying row 2 and column 2 of (2) by a scaling factor β that describes the ratio of internal impedance to terminal impedance. The result obtained after multiplying the scaling factor is given by (3).

(3)

(Y)=jYo1(-cot θ01β·csc θ010β·csc θ01-β2·(cot θ01+cot θ02)β·csc θ020β·csc θ02-cot θ02).

The internal impedance converted circuit can be implemented as a transmission line circuit in which stubs are connected in parallel to each port. Its equivalent circuit is illustrated in Fig. 1(c). The admittance parameters of this equivalent circuit can be expressed as

(4)

(Y)EQ=j(-Yo1Tcotθ01TYo1Tcscθ01T0Yo1Tcscθ01T-Yo1Tcotθ01T-Yo2Tcotθ02TYo2Tcscθ02T0Yo2Tcscθ02T-Yo2Tcotθ02T) +j(B1000B2000B3).

Because (3) and (4) should be the same as those for equivalent circuits, the following expression can be obtained.

(5a)

B1-Yo1Tcotθ01T=-Yo1cotθ01

(5b)

Yo1T csc θ01T=β·Yo1 csc θ01

(5c)

B2-(Yo1T cot θ01T+Yo2T cot θ02T)=-β2·Yo1(cot θ01+cot θ2)

(5d)

Yo2T csc θ02T=β·Yo1 csc θ02

(5e)

B3-Yo2T cot θ02T=-Yo1 cot θ02

The susceptance B_i (i = 1, 2, 3) can be implemented in open-or short-circuit stubs with admittance values and electrical length indicated in (6).

(6a)

Bi=Yopen-stub tanθopen-stub

(6b)

Bi=-Yshort-stub cotθshort-stub

In (5b) and (5d), if the conditions satisfy the relation,

(7)

β>sin θ01sin θ01T and β>sin θ02sin θ02T,

the admittances Y_o1, Y_o1_T, and Y_o2_T will have the following relationship:

(8)

Yo1T>Yo1,Yo2T>Yo1.

This means that if condition (7) is satisfied, the transmission line of the equivalent circuit in Fig. 1(c) can be converted to obtain an impedance value lower than the original one.

In addition, if the conditions satisfy the relation,

(9)

β<sin θ01sin θ01T and β<sin θ02sin θ02T,

the transmission line of the equivalent circuit can be converted into a line with an impedance value higher than the original one.

To obtain B₁, B₂, and B₃, the conditions of (5b) and (5d) are substituted into (5c), and the result is as follows:

(10)

B1=Yo1T cot θ01T-Yo1 cot θ01

(11)

B2=β·Yo1[cos θo1T·csc θo1(1-β·cos θo1·sec θo1T)+cos θ02T·csc θo2(1-β·cos θo2·sec θ02T)]

(12)

B3=Yo2T cot θ02T-Yo1 cot θ02

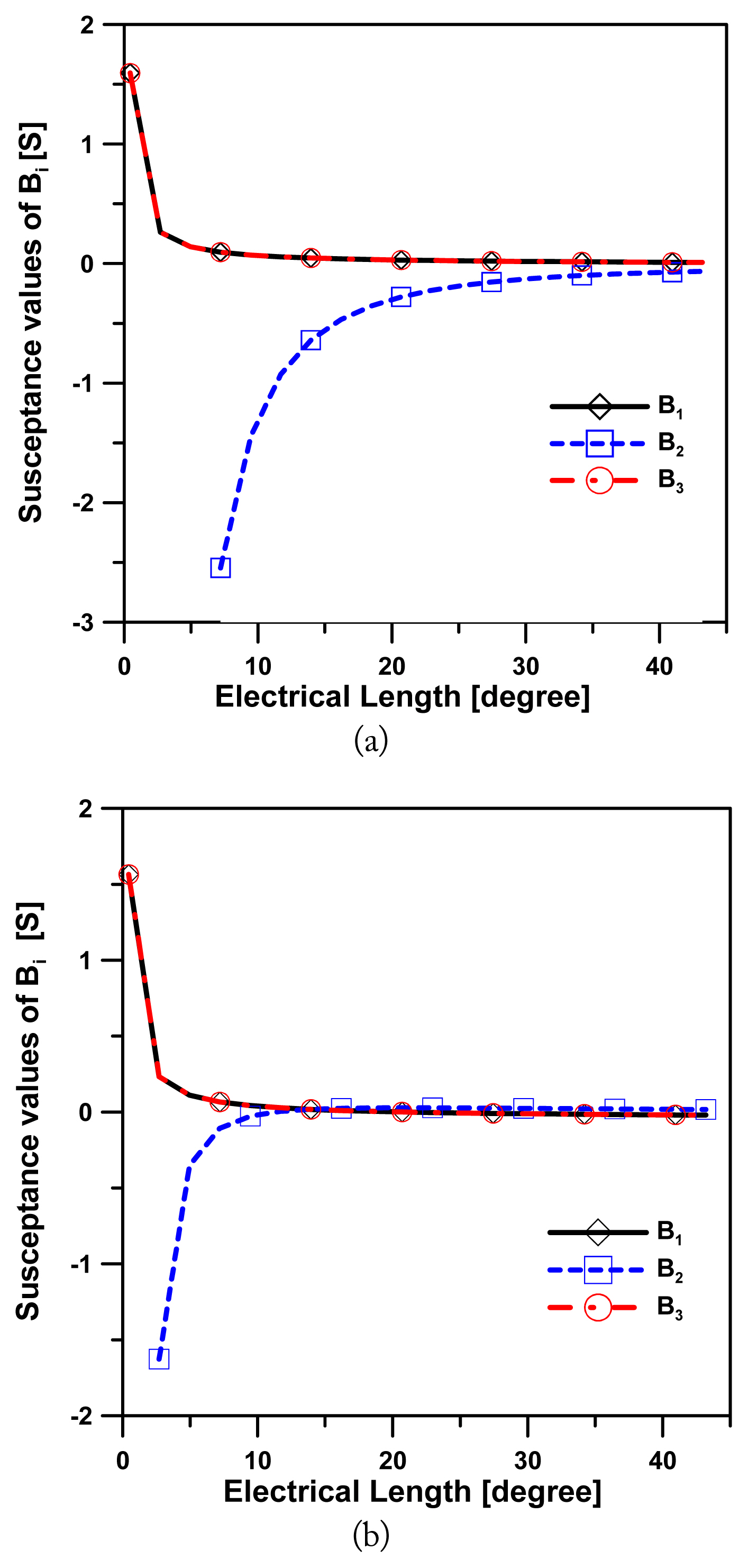
Fig. 2(a) displays the variation of B₁, B₂, and B₃ when θ_o1_T and θ_o2_T change from 0°–45° under characteristic admittances Y_o1 = 0.003663 S and Y_o₁_T = 0.01254 S, with electrical lengths θ_o1 = θ_o2 = 45°. Furthermore, Fig. 2(b) shows the variation of B₁, B₂, and B₃ when θ_o1_T and θ_o2_T change from 0°–45° under characteristic admittances Y_o₁ = 0.03289 S and Y_o₁_T = 0.01254 S, with electrical lengths θ_o1 = θ_o2 = 45°.

III. Simulation and Experimental Results

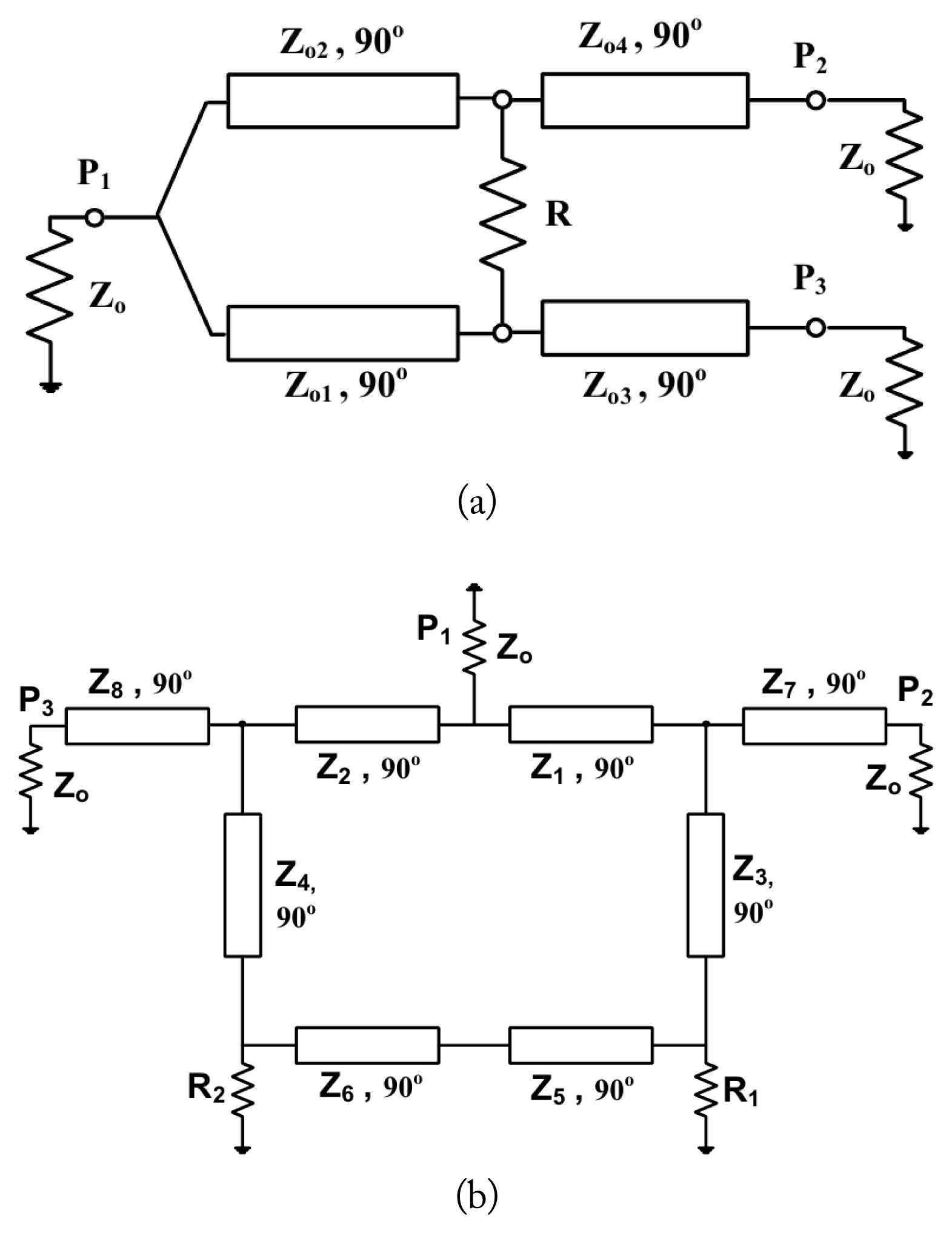
Fig. 3 presents the schematics of a Wilkinson power divider and a Gysel power divider with splitting ratio of 9:1 and 5:1, respectively. The impedance values of each quarter-wavelength transmission line are provided in Tables 1 and 2.

To design high- and low-impedance transmission lines in Tables 1 and 2 using the impedance control method, a Rogers printed circuit board with a dielectric constant of 3.48, a dielectric thickness of 0.762 mm, and a copper thickness of 0.035 mm was used.

The simulation was performed using Microwave Office software version 13 developed by Cadence Design Systems Inc.

In the Wilkinson power divider, first, for the transmission line of 273.8 Ω with θ_o1 = θ_o2 = 45°, a microstrip line width capable of implementing this line was selected as 0.7 mm (characteristic impedance of 79.7 Ω), and the electrical lengths were determined to be θ_o1_T = θ_o2_T = 36°. The scaling factor of this design condition was β = 4.13348, and its susceptance values were calculated as B₂ = −0.09024 and B₁ = B₃ = 0.01362.

Because B₂ is negative, the short-circuit stub was implemented at a line width of 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 6.3° using 0.4 mm via holes. Further, because the B₁ and B₃ values are positive, the line width of the open-circuit stub was implemented at 3.5 mm (characteristic impedance of 30.5 Ω) and an electrical length of 22.5°.

Second, for the transmission line of 30.4 Ω with θ_o1 = θ_o2 = 45°, a microstrip line width capable of implementing this line was selected as 0.7 mm (characteristic impedance of 79.7 Ω), while the electrical lengths were determined to be θ_o1_T = θ_o2_T = 31.5°. The scaling factor of this design condition was β = 0.51666, and its susceptance values were calculated as B₂ = 0.0234 and B₁ = B₃ = −0.01239.

Using the B₂ value, the line width of the implemented open-circuit stub was implemented at 3.5 mm (characteristic impedance of 30.5 Ω) and an electrical length of 35.5°.

In addition, using the B₁ and B₃ values, the line width of the short-circuit stub was implemented at 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 38.9° with 0.4 mm via holes.

At the intersection point of Z_o1 and Z_o2, the open-circuit stub susceptance with B₁ = 0.01362 at Z_o1 and the short-circuit stub susceptance with B₁ = −0.01239 at Z_o2 meet; therefore, we can implement the difference between the two values, i.e., susceptance B_x = 0.00123. For this susceptance, the open-circuit stub has a line width of 1.2 mm (characteristic impedance of 60.9 Ω) and an electrical length of 4.3°.

In the Gysel power divider, first, for the transmission line of 183.1 Ω with θ_o1 = θ_o2 = 45°, a microstrip line width of 0.7 mm was selected, which was capable of implementing this line (characteristic impedance of 79.7 Ω), and the electrical lengths were determined to be θ_o1_T = θ_o2_T = 31.5°. The scaling factor of this design condition was β = 3.10962, and its susceptance values were calculated as B₂ = −0.06465 and B₁ = B₃ = 0.01501.

Because B₂ is negative, the short-circuit stub was implemented at a line width of 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 2.4° using 0.4 mm via holes. Further, because the B₁ and B₃ values are positive, the line width of the open-circuit stub was implemented at 3.5 mm (characteristic impedance of 30.5 Ω) and an electrical length of 39°.

Second, for the transmission line of 111.8 Ω with θ_o1 = θ_o2 = 45°, a microstrip line width capable of implementing this line was selected as 0.7 mm (characteristic impedance of 79.7 Ω), and the electrical lengths were determined to be θ_o1_T = θ_o2_T = 31.5°. The scaling factor of this design condition was β = 1.89833, and its susceptance values were calculated as B₂ = −0.02352 and B₁ = B₃ = 0.01153.

Because B₂ is negative, the short-circuit stub was implemented at a line width of 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 23.1° using 0.4 mm via holes. Further, because the B₁ and B₃ values are positive, the line width of the open-circuit stub was implemented at 3.5 mm (characteristic impedance of 30.5 Ω) and an electrical length of 35.1°.

Third, for the transmission line of 36.6 Ω with θ_o1 = θ_o2 = 45°, a microstrip line width capable of implementing this line was selected as 0.7 mm (characteristic impedance of 79.7 Ω), and the electrical lengths were determined to be θ_o1_T = θ_o2_T = 27°. The scaling factor of this design condition was β = 0.71577, and its susceptance values were calculated as B₂ = 0.02127 and B₁ = B₃ = −0.00268.

Because B₁, and B₃ are negative, the short-circuit stub was implemented at a line width of 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 23.7° using 0.4 mm via holes. Further, because B₂ is positive, the line width of the open-circuit stub was implemented at 3.5 mm (characteristic impedance of 30.5 Ω) and an electrical length of 33°.

Fourth, for the 22.4 Ω transmission line with θ_o1 = θ_o2 = 45°, a microstrip line width capable of implementing this line was selected as 0.7 mm (characteristic impedance of 79.7 Ω), and the electrical lengths were determined to be θ_o1_T = θ_o2_T = 27°. The scaling factor of this design condition was β = 0.43697, and its susceptance values were calculated as B₂ = 0.03217 and B₁ = B₃ = −0.02010.

Because B₁, and B₃ are negative, the short-circuit stub was implemented at a line width of 0.4 mm (characteristic impedance of 99.8 Ω) and an electrical length of 23.7° using 0.4 mm via holes. Further, because B₂ is positive, the line width of 3.5 mm of the open-circuit stub was implemented (characteristic impedance of 30.5 Ω) and an electrical length of 44.5°.

Fig. 4 depicts a photograph of the devised unequal Wilkinson power divider after the optimization process. Because there is no standard resistance value, the isolation resistance is implemented by connecting 150 Ω and 15 Ω in series.

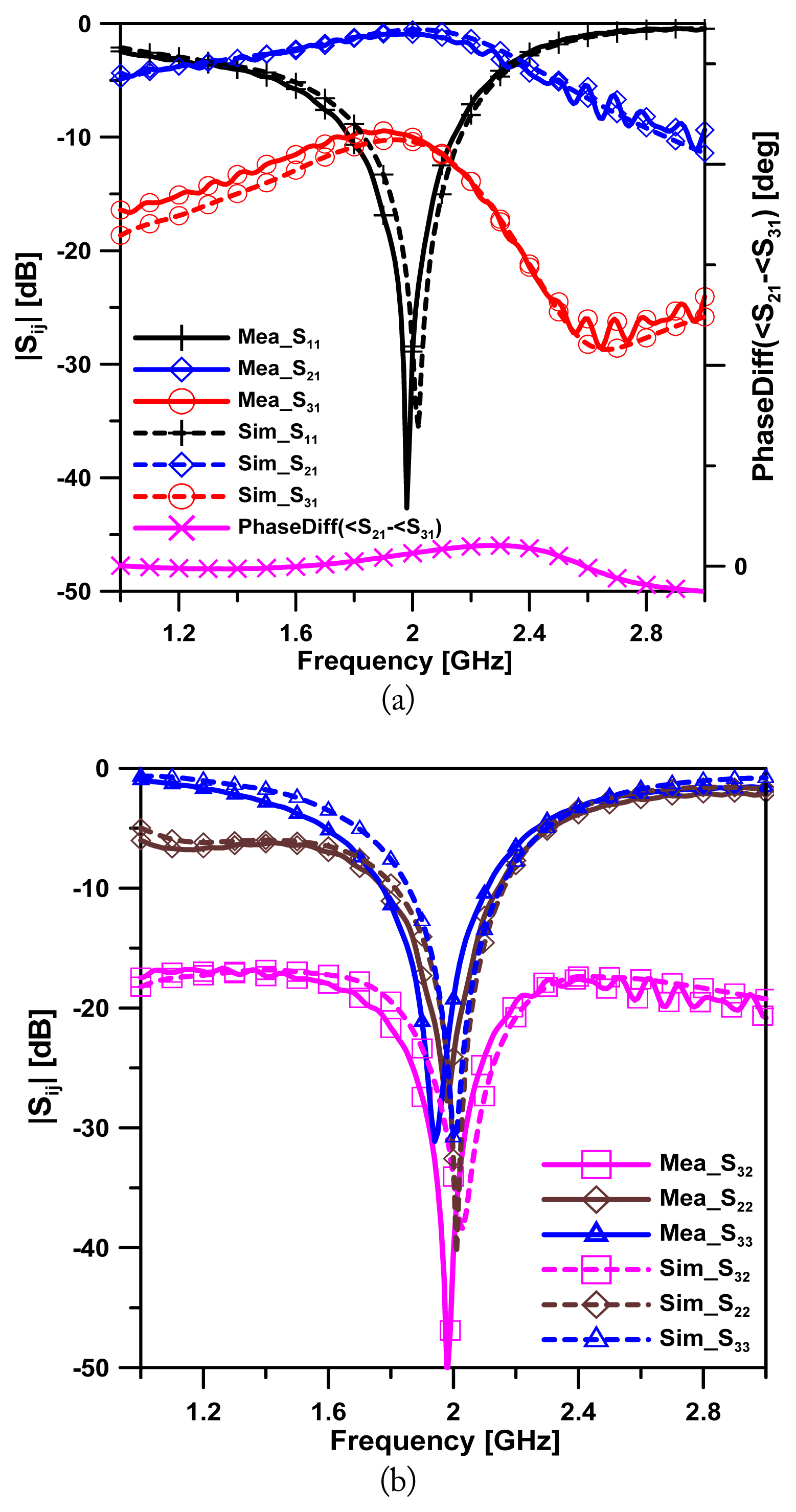
Fig. 5 shows the S-parameters of the simulated and measured unequal Wilkinson power dividers. The insertion losses of |S₂₁| and |S₃₁| were −0.96 dB and −10.01 dB, respectively. Furthermore, the isolation of |S₃₂| was greater than 35 dB. The input return loss of |S₁₁| was less than −25 dB and the output return losses of |S₂₂| and |S₃₃| were less than −20 dB at a center frequency of 2 GHz. The measured −15dB bandwidth of |S₁₁| was in the range of 1.88 to 2.08 GHz, featuring a fractional bandwidth of 10%. In addition, the phase difference between the output ports was measured within ±15°.

In addition, Fig. 6 depicts a photograph of the fabricated unequal Gysel power divider after the optimization process. Because there is no standard resistance value, the isolation resistance is implemented by connecting 100 Ω and 47 Ω, in series, and 22 Ω.

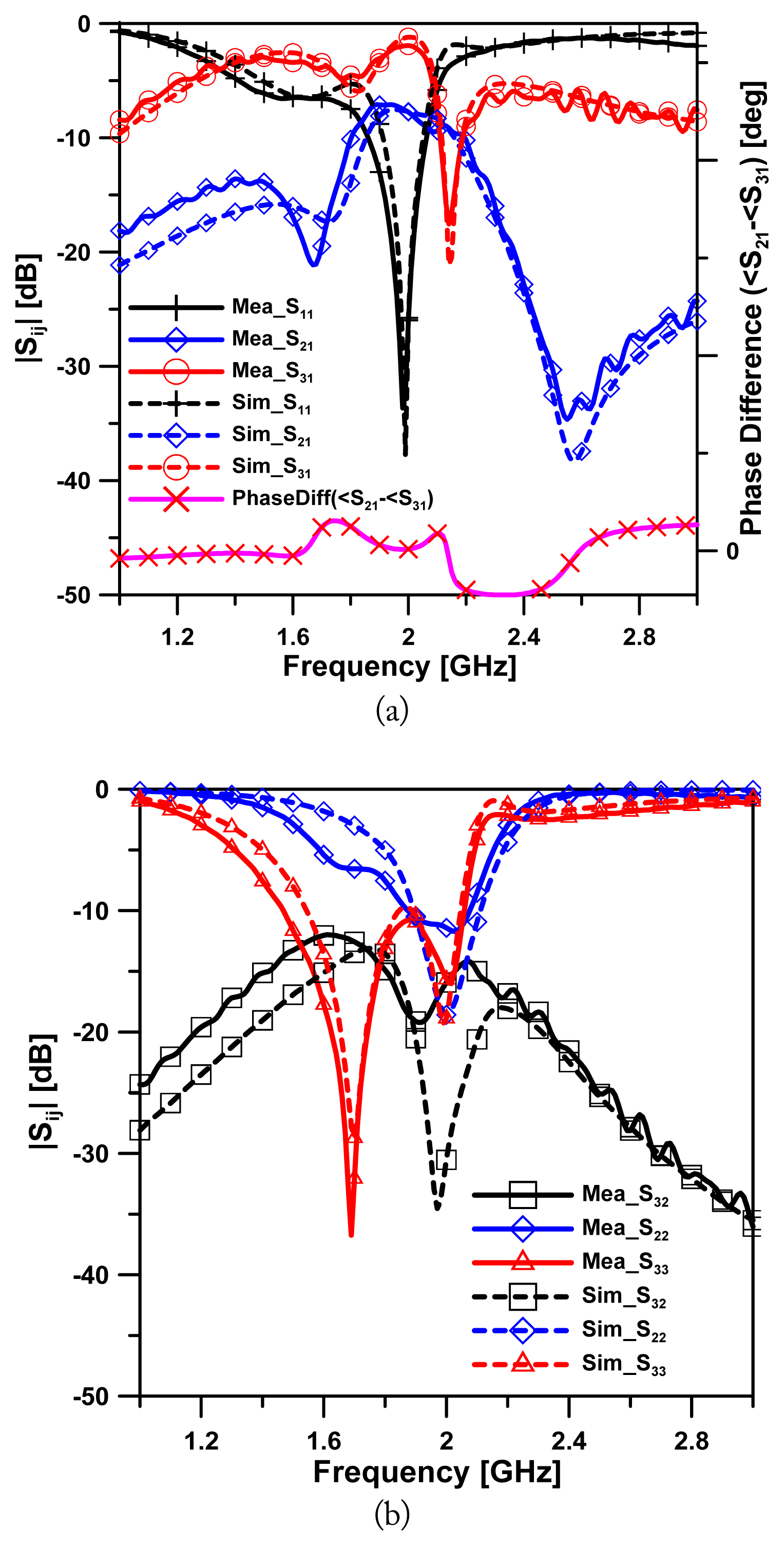
Fig. 7 displays the S-parameters of the simulated and measured unequal Gysel power dividers. The insertion losses of |S₂₁| and |S₃₁| were −1.92 dB and −7.74 dB, respectively. Furthermore, the isolation of |S₃₂| was greater than 15 dB. The input return loss of |S₁₁| was less than −25 dB, and the output return losses of |S₂₂| and |S₃₃| were less than −10 dB at a center frequency of 2 GHz. The measured −15dB bandwidth of |S₁₁| was in the range of 1.91 to 2.03 GHz, featuring a fractional bandwidth of 6%. In addition, the phase difference between the output ports was measured within ±4°.

It can be observed that these measurement results are almost identical to the simulation results in Figs. 5 and 7. Table 3 shows a comparison of the proposed divider to the conventional unequal divider.

IV. Conclusion

This study applied an impedance control method to the design of a Wilkinson and a Gysel power divider with splitting ratios of 9:1 and 5:1, respectively. In this method, the high impedance line was separated into two lines, and open- and short-circuit stubs were connected to three ports in parallel. This method is considerably more convenient than the conventional one using thick materials to implement high-impedance lines.

The method presented here, which can easily implement high-impedance lines, can be used for the design of various parts.

Fig. 1

(a) Arbitrary transmission line, (b) transmission line with port added in the middle, (c) equivalent circuit to (b).

Fig. 2

(a) Variation of B₁, B₂, and B₃ according to θ_o1_T, and θ_o2_T at admittances Y_o1 = 0.003663 S and Y_o₁_T = 0.01254 S, and electrical lengths θ_o₁ = θ_o₂ = 45°. (b) Variation of B₁, B₂, and B₃ according to θ_o1_T, and θ_o2_T at admittances Y_o1 = 0.03289 S and Y_o1_T = 0.01254 S, and electrical lengths θ_o1 = θ_o2 = 45°.

Fig. 3

Schematic of (a) unequal Wilkinson power divider and (b) unequal Gysel power divider.

Fig. 4

Photograph of the proposed Wilkinson power divider.

Fig. 5

Simulated and measured S-parameters of the proposed Wilkinson power divider: (a) |S₁₁|, |S₂₁|, |S₃₁|, and phase difference (∠S₂₁–∠S₃₁) and (b) |S₃₂|, |S₂₂|, and |S₃₃|.

Fig. 6

Photograph of the proposed Gysel power divider.

Fig. 7

Simulated and measured S-parameters of the proposed Gysel power divider: (a) |S₁₁|, |S₂₁|, |S₃₁|, and phase difference (∠S₂₁–∠S₃₁) and (b) |S₃₂|, |S₂₂|, and |S₃₃|.

Table 1

Impedance values of unequal Wilkinson power dividers with a 9:1 splitting ratio

Parameter	Value
Z_o1 (Ω)	273.8
Z_o2 (Ω)	30.4
Z_o3 (Ω)	86.6
Z_o4 (Ω)	28.8
R (Ω)	167

Table 2

Impedance values of unequal Gysel power dividers with a 5:1 splitting ratio

Parameter	Value	Parameter	Value
Z₁ (Ω)	183.1	Z₆ (Ω)	22.4
Z₂ (Ω)	36.6	Z₇ (Ω)	74.8
Z₃ (Ω)	111.8	Z₈ (Ω)	33.5
Z₄ (Ω)	22.4	R₁ (Ω)	111
Z₅ (Ω)	111.8	R₂ (Ω)	22

Table 3

Comparison of the proposed divider to the conventional unequal divider

Ref.	Center freq. (GHz)	Dividing ratio	Implement method	Insertion loss (dB)
[7]	1.5	1:4	DGS	−1.0 / −7.0
[9]	0.8–2.27	1:2	Microstrip/slotline	−2.09 / −5.41
[10]	2	1:10	Coupled lines	−0.75 / −10.3
[11]	1	1:10	Capacitive loaded TL	−0.77 / −9.7
This work	2	1:9	Open/short-stub	−0.96 / −10.1
This work		1:5		−1.9 / −7.7

References

1. H Jang, P Roblin, C Quindroit, Y Lin, and RD Pond, "Asymmetric Doherty power amplifier designed using model-based nonlinear embedding," IEEE Transactions on Microwave Theory and Techniques, vol. 62, no. 12, pp. 3436–3451, 2014.

2. RC Hansen, Phased Array Antennas. Hoboken, NJ: John Wiley & Sons, 2009.

3. R Sinha, A De, and S Sanyal, "A theorem on asymmetric structure based rat-race coupler," IEEE Microwave and Wireless Components Letters, vol. 25, no. 3, pp. 145–147, 2014.

4. CJ Chen, "Analytical derivation of T-shaped structures for synthesis of quarter-wavelength transmission lines," IEEE Microwave and Wireless Components Letters, vol. 23, no. 10, pp. 524–526, 2013.

5. KO Sun, SJ Ho, CC Yen, and D Van Der Weide, "A compact branch-line coupler using discontinuous microstrip lines," IEEE Microwave and Wireless Components Letters, vol. 15, no. 8, pp. 519–520, 2005.

6. CW Tang, CT Tseng, and KC Hsu, "Design of wide pass-band microstrip branch-line couplers with multiple sections," IEEE Transactions on Components, Packaging and Manufacturing Technology, vol. 4, no. 7, pp. 1222–1227, 2014.

7. JS Lim, SW Lee, CS Kim, JS Park, D Ahn, and S Nam, "A 4.1 unequal Wilkinson power divider," IEEE Microwave and Wireless Components Letters, vol. 11, no. 3, pp. 124–126, 2001.

8. RK Mongia, IJ Bahl, and P Bhartia, RF and Microwave Coupled-Line Circuits. Boston, MA: Artech House, 1999.

9. F Lin, QX Chu, Z Gong, and Z Lin, "Compact broadband Gysel power divider with arbitrary power-dividing ratio using microstrip/slotline phase inverter," IEEE Transactions on Microwave Theory and Techniques, vol. 60, no. 5, pp. 1226–1234, 2012.

10. B Li, X Wu, and W Wu, "A 10:1 unequal Wilkinson power divider using coupled lines with two shorts," IEEE Microwave and Wireless Components Letters, vol. 19, no. 12, pp. 789–791, 2009.

11. Y Kim, "A 10:1 unequal Gysel power divider using a capacitive loaded transmission line," Progress in Electromagnetics Research, vol. 32, pp. 1–10, 2012.

12. Q Wu, Y Yang, Y Wang, X Shi, and M Yu, "General model for loaded stub branch-line coupler," In: Proceedings of 2016 IEEE MTT-S International Microwave Symposium (IMS); San Francisco, CA. 2016, pp 1–4.

13. Q Wu, Y Yang, Y Wang, X Shi, and M Yu, "Characteristic impedance control for branch-line coupler design," IEEE Microwave and Wireless Components Letters, vol. 28, no. 2, pp. 123–125, 2018.

Biography

Young-Chul Yoon received his B.S., M.S., and Ph.D. in electronics engineering from Sogang University, Seoul, South Korea in 1978, 1982, and 1989, respectively. In 1987, he joined the Department of Electronics Engineering, Catholic Kwandong University, Gangneung, South Korea, where he is currently a professor. His areas of interest are the design of high-power amplifiers for the ISM band, and RF and microwave circuit analysis and design.

Biography

Young Kim received his B.S., M.S., and Ph.D. in electronics engineering from Sogang University, Seoul, South Korea in 1986, 1988, and 2002, respectively. He developed cellular and PCS linear power amplifiers at Samsung Electronics Co. Ltd. In 2003, he joined the School of Electronics Engineering, Kumoh National Institute of Technology, Gumi, South Korea, where he is currently a professor. His areas of interest are the design of high-power amplifiers and linearization techniques, and RF and microwave circuit analysis and design.