I. Introduction
In telecommunications, geophysical explorations, and diagnostics, insulated cylindrical antennas have often been located in lossy media such as soil, water, or biological tissue [1]. The electromagnetic characteristics of antennas and wave propagation in inhomogeneous media have been analyzed using the finite-difference time-domain (FDTD) method [1ŌĆō4]. However, since the standard FDTD is based on the time and space discretization of MaxwellŌĆÖs equations, the fine geometries of the antennas should be modeled as fine grids with sufficiently small cell sizes relative to the minimum wavelength. This results in low computational efficiency due to the large number of cells. One the other hand, thin-wire FDTD (TW-FDTD) treats a coarse grid with the pre-correction of near-field behavior around thin electrically insulated antennas [3, 4]. Therefore, TW-FDTD can provide sufficient accuracy, equivalent to finegrid FDTD, while maintaining higher computational efficiency. In [3, 4], the loading effect of both the insulation and surrounding media was considered by using discrete-time boundary condition (DTBC) formulations. These were derived from the dielectric constitutive relation on the material interface between the lossy media under the uniform field approximation (UFA) over each time step. However, the electromagnetic fields on the material interface are fast varying, and the standard FDTD method is based on the linear field approximation (LFA) in time and space. Therefore, the LFA over each time interval may be suitable for the DTBC formulation. In this paper, we propose an improved DTBC by using a discrete-time version of MaxwellŌĆÖs equations under the LFA. The DTBC is corrected in the TW-FDTD update equation. By comparing the input impedances of Teflon-insulated cylindrical monopole antennas located in wet soil, we show that this approach is more accurate than previous techniques.
II. Improved DTBC Formulation for TW-FDTD
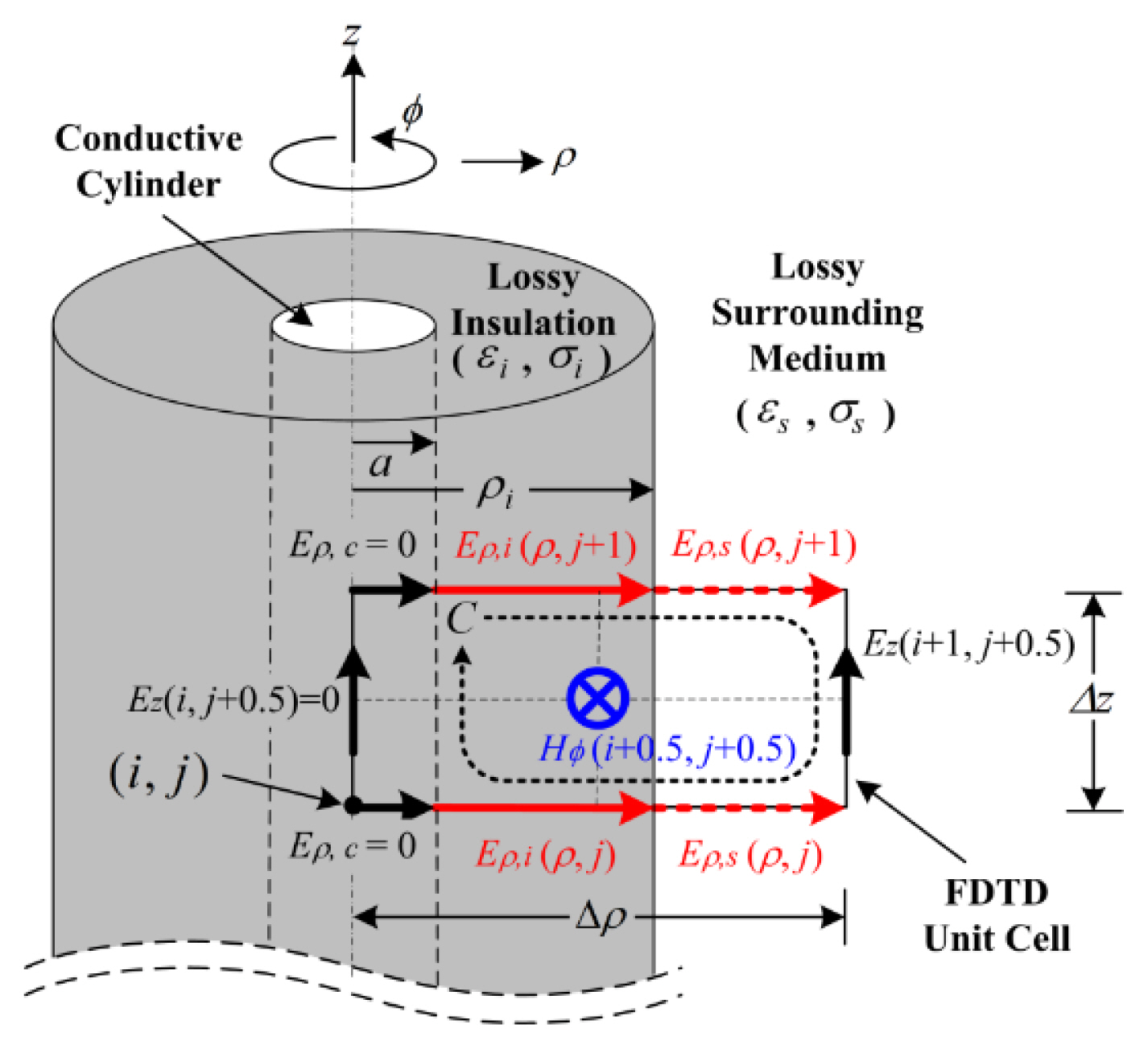
Fig. 1 shows a FDTD unit cell for the TW modeling of a lossy insulated cylinder in a lossy surrounding medium. A conductive cylinder of outer radius a lies along the z-axis and is insulated with a lossy dielectric material of outer radius Žüi, permittivity ╔øi, and conductivity Žāi. The insulated cylinder is surrounded by a lossy dielectric medium of permittivity ╔øs and conductivity Žās. Since the geometry of the cylinder is rotationally symmetric along the Žå-direction, we use the two-dimensional (2D) cylindrical FDTD of the discrete space (Žüz) = (i╬öŽü, j╬öz) ŌēĪ (i,j) and discrete time t = n╬öt ŌēĪ n [4]. Here, ╬öŽü and ╬öz are the spatial steps along the Žü and z axes, respectively, and ╬öt is the time step. The variables (i,j) and n are the integer indices of the space and time discretization, respectively.
The LFA over each time step can be represented as the central-difference and the time-averaging schemes in the differential form of Ampere-MaxwellŌĆÖs law at t = (n ŌłÆ 0.5)╬öt as
(1)
In Fig. 1, the tangential electric and magnetic fields on the material interface (Žü = Žüi) between the insulating and the surrounding media should be continuous:
where the subscripts i and s denote the insulating and surrounding media, respectively. Applying (2) and (3) to (1), an improved DTBC for the discontinuity of the normal electric fields on the interface can be obtained:
(4)
From (4), the normal electric field at t = nΔt in the surrounding medium on the interface can be given as
In (5), the first term on the right-hand side is the DTBC of the present time t = n╬öt, and the second term is the DTBC that includes the convolution effects of past times t = (n ŌłÆ 1) ╬öt,ŌĆ”, ╬öt, and 0. Table 1 shows a comparison of the DTBC coefficients used in previous versions of the technique and the proposed TW-FDTD framework. All TW-FDTD equations, except for those for the DTBC coefficients, are the same as those in [4]. Therefore, they were omitted here for brevity.
III. Comparison Results
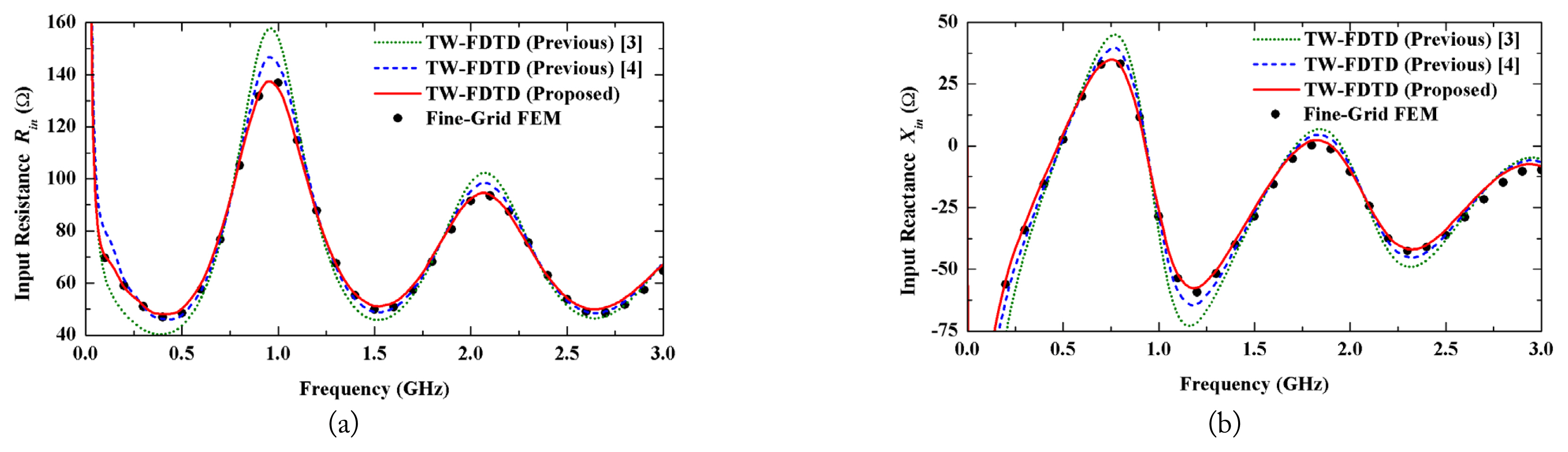
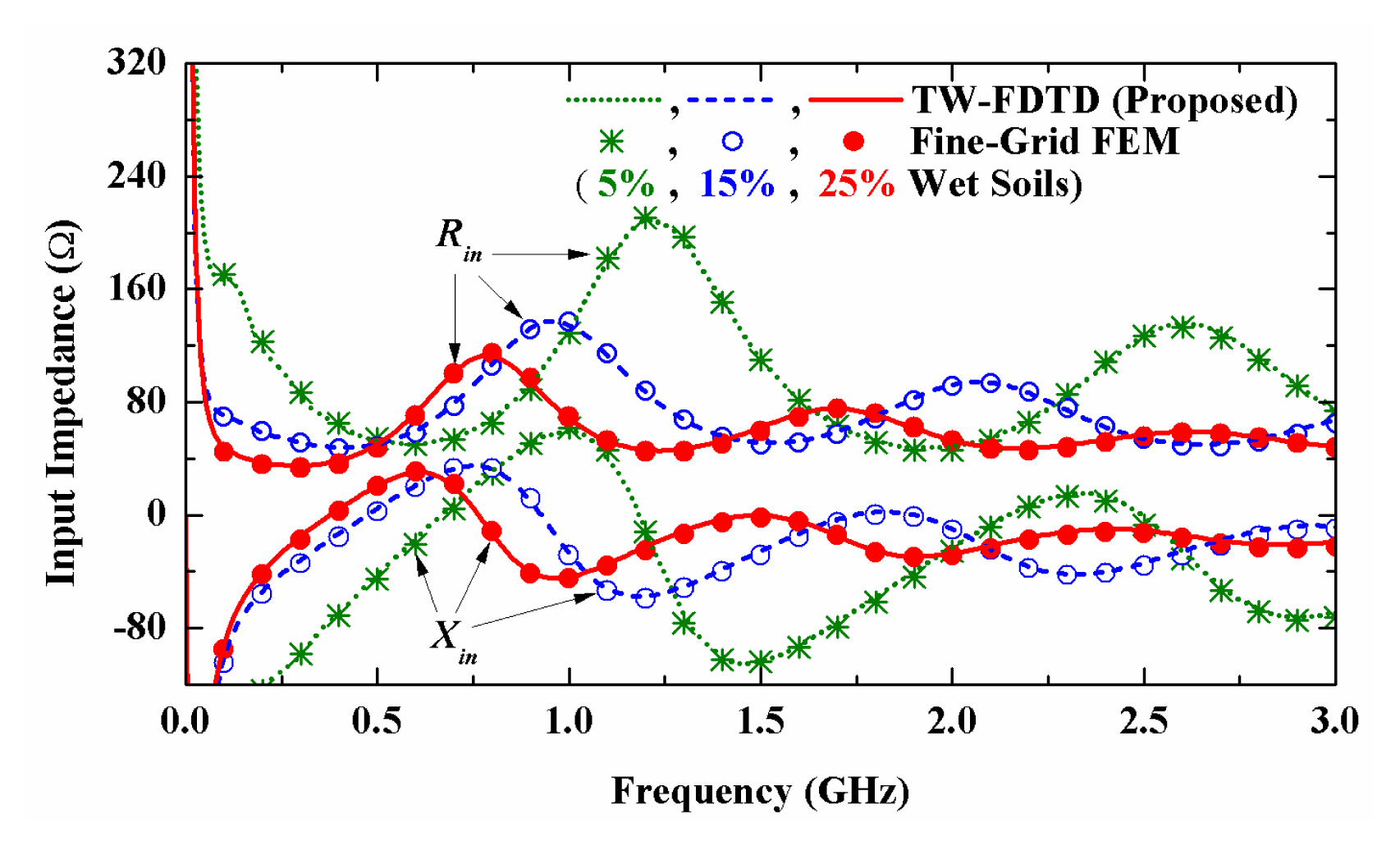
To evaluate the computational accuracy of the proposed TW-FDTD technique using the improved DTBC formulation, we calculate the input impedances (Zin = Rin+jXin) of Teflon-insulated cylindrical monopole antennas in wet soils. The conductive cylinder of an antenna has a = 0.635 mm, an axial length of 100a, and Žüi = 1.614a and is insulated with Teflon (╔øi = 2.1╔ø0, Žāi = 5.0 ╬╝S/m [4]). The insulated antennas are surrounded by 5%ŌĆō25% wet soil and are fed by a 50 ╬® coaxial line. In all FDTD simulations, the spatial steps along the radial and axial directions are ╬öŽü = 3.23a and ╬öz = a, respectively. Under the stability condition, we use a time step of ╬öt = min(╬öŽü, ╬öz)/2v, where v is the wave velocity in the medium. First, in the case of the Teflon-insulated monopole antenna inserted in 15% wet soil (╔øs = 5.3╔ø0 and Žās = 0.117 S/m [5]), the results of our approach are compared with those of previous TW-FDTD formulations [3, 4] and with fine-grid finite-element method (FEM) data, as shown in Fig. 2. It can be seen that the results of previous TW-FDTD models show some errors compared with the FEM data. This is because [3] and [4] are based on the first-term DTBC and full-term DTBC under the UFA over each time step, respectively. Since the proposed TW-FDTD technique uses the full-term DTBC under the LFA over each time interval, it provides high accuracy, comparable with the FEM data. Next, the effect of the wet soil as a function of the volumetric moisture content is investigated, as shown in Fig. 3. We calculate the input impedances of the Teflon-insulated monopole antennas inserted in 5%ŌĆō25% wet soils (╔øs = 2.8 ╔ø0 ŌĆō 10.2╔ø0 and Žās = 0.039 ŌĆō 0.218 S/m [5]). One can observe that the results of the proposed TW-FDTD model are in good agreement with the FEM data.
IV. Conclusion
An improved DTBC formulation for the TW-FDTD modeling of insulated antennas located in lossy media is proposed. The improved DTBC between the insulation and surrounding media was derived from MaxwellŌĆÖs equations under the LFA over each time step. Then, the DTBC was corrected in the TW-FDTD equations. In a comparative study of the input impedances of Teflon-insulated monopole antennas in wet soils, we show that the proposed approach has higher accuracy than previous techniques.