Analytical Dispersion Equations of a Lossy Coaxial Waveguide in the Microwave and Visible Spectra

Article information

Abstract

I. Introduction

A coaxial waveguide is a fundamental transmission line to stably guide a light for optoelectronics [1–3] or precisely measure the reflection coefficient and impedance up to millimeter-wave bands [4, 5]. Accurate evaluation of wave propagation through a practical coaxial waveguide is essential for quantifying measurement uncertainty occurring in microwave transmission [5]. Even in the visible spectrum, a nanocoax [3] is one of the promising structures for low-loss propagation composed of plasmonic and photonic modes, where the permittivity can be negative or complex to model real metals at optical frequency.

Since a practical coaxial line is inherently lossy owing to finite electrical conductivity, the TM wave (E_z ≠ 0, H_z = 0) instead of the TEM wave (E_z = 0, H_z = 0) propagates and is gradually decreased in the z-direction. This behavior makes the dispersion analysis of the lossy coaxial waveguide more involved. Therefore, it is of great importance to derive and formulate an exact and rigorous dispersion relation of the lossy coaxial waveguide, which can be modeled as a multilayered dielectric coaxial waveguide [1, 6–8]. A dielectric coaxial waveguide was analyzed using the boundary conditions of an open region [6] and an infinitely lossy outer conductor [7, 8]. In the following sections, we apply a standard mode-matching technique [9] for analyzing a dielectric coaxial waveguide surrounded by the perfect electric conductor (PEC) boundary. A newly-derived rigorous dispersion relation is used to determine precise complex propagation constants for the hybrid, TM, and TE modes in microwave and optical spectra, where we use Davidenko’s method [10, 11] for searching complex roots.

Using the conductor condition or high permittivity approximation, we obtained simplified but accurate dispersion equations useful for characterizing the transmission behaviors of the lossy coaxial waveguide. This means that our rigorous dispersion equations can be utilized to generate the field distributions for the TM_0p, TE_0p, EH_mp, and HE_mp modes and formulate the scattering characteristics of canonical coaxial structures used in a coaxial calibration kit [5]. The quasi-TEM mode also yields a closed-form approximate solution for the TM₀₁-mode complex propagation constant, which becomes identical to the propagation constant [5, 7] in the high electrical conductivity limit.

II. Mode-Matching Analysis

A lossy coaxial waveguide can be modeled using a multilayered dielectric coaxial waveguide [1, 6–8] as shown in Fig. 1, where the medium constants—ε₁, ε₂, ε₃ and μ₁, μ₂, μ₃—can be any complex number. We use and omit e^i(βz–ωt) for the time convention, where β is a complex propagation constant composed of phase (ℜ[β]) and attenuation (ℑ[β]) constants. The interesting point of the geometry shown in Fig. 1 is that a dielectric coaxial waveguide [1, 6–8] shown in Fig. 2 is entirely surrounded by the PEC boundary. It is known that unwanted multiple leaky modes [11] are inevitably generated in open magnetodielectric waveguides including dielectric coaxial structures [1, 6] with an open boundary as shown in Fig. 2. The existence of leaky phenomena caused by the open boundary makes a dispersion analysis of the dielectric coaxial waveguide much more involved. For instance, the dielectric coaxial waveguide shown in Fig. 2 should satisfy a leaky dispersion relation in an open region as

Fig. 1

Modeling of a lossy coaxial waveguide using a multilayered dielectric coaxial waveguide surrounded by the perfect electric conductor (PEC) boundary.

Fig. 2

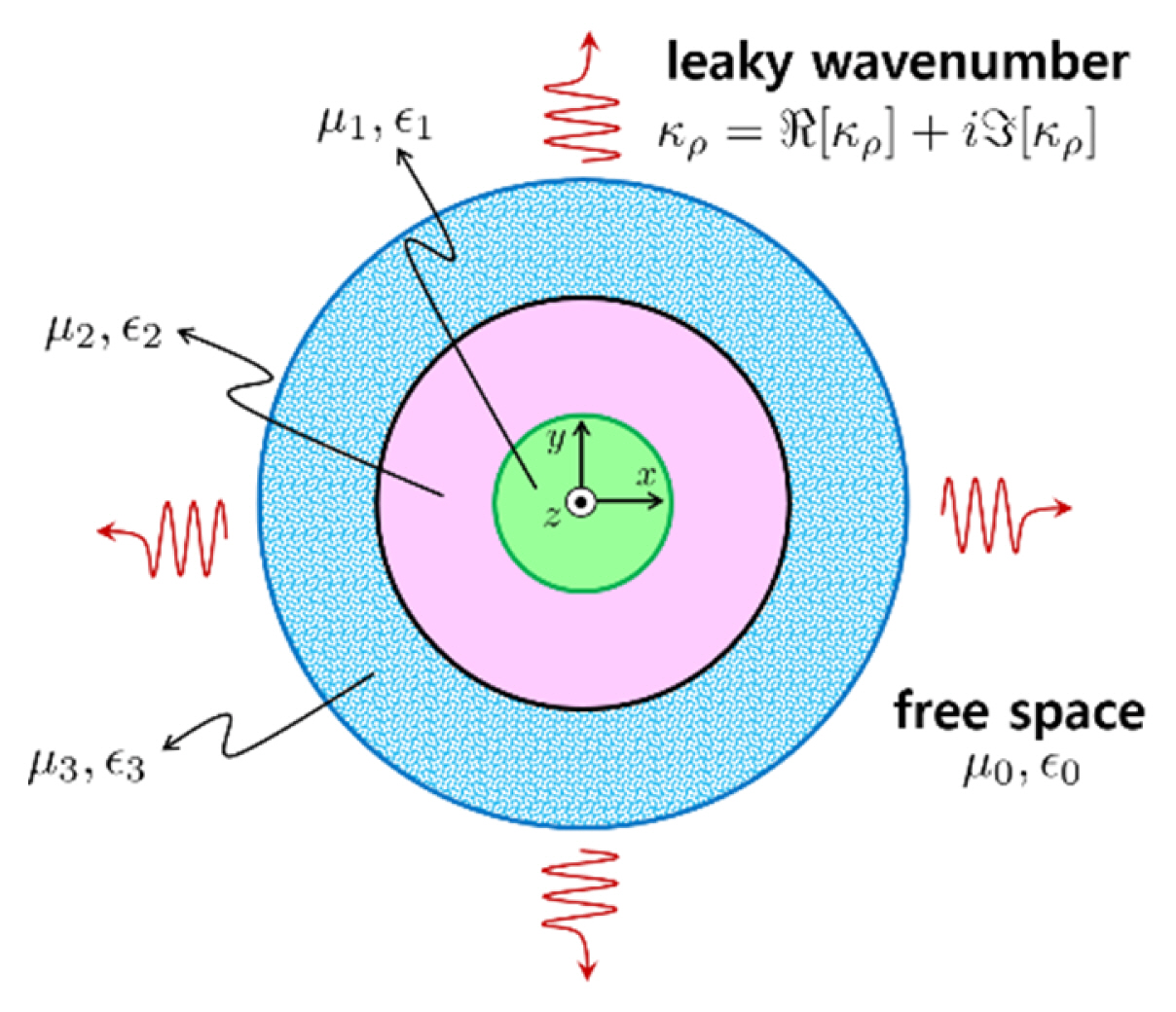
The geometry of a three-layered dielectric coaxial waveguide placed in free space or with an open boundary.

where k0=ωμ0ɛ0, and κ_ρ is a leaky wavenumber for a radial direction ρ=x2+y2. Equating the imaginary parts of the left and right sides of Eq. (1) yields a leaky-wave relation for κ_ρ and β as

where the phase term of a guided wave is e^{i(κ_ρρ+βz)}. Eq. (2) indicates that the radial and longitudinal radiation conditions of κ_ρ and β cannot be satisfied at the same time, owing to the fact that the signs of the real or imaginary parts of κ_ρ and β are always different from each other. Contrary to the geometry shown in Fig. 2, the PEC boundary and lossy region (III) introduced in Fig. 1 enable us to block the leaky modes completely and model the conductor loss precisely. This is because the PEC boundary at ρ = b + d is imposed and ε₃ can be complex, thus confirming there are no leaky modes and the waves are evanescent in region (III). Therefore, the field representations for regions (I) through (III) as shown in Fig. 1 are formulated using magnetic and electric vector potentials [9]:

where A_m, B_m, Em(1),(2),Fm(1),(2), G_m, and H_m are the unknown modal coefficients for the mth azimuthal mode, ρ=x2+y2, φ = tan⁻¹(y/x), κn=kn2-β2, kn=ωμnɛn,

and (·)′ denotes differentiation for the entire argument; J_m(·) and N_m(·) are the mth order Bessel functions of the first and second kinds, respectively. Based on the standard mode-matching analysis [9], we enforce E_z-, E_φ-, H_z-, and H_φ-field continuities at ρ = a and b for the mth azimuthal mode. First, by multiplying the E_z- and H_z-field continuities at ρ = a by e^−ilφ (l = 0, ±1, ±2, ···) and integrating over 0 ≤ φ ≤ 2π yields, respectively, we get:

where u_n = κ_na,

Next, we apply and integrate the E_φ- and the H_φ-field continuities at ρ = a with e^−ilφ to obtain the additional field-matching equations, respectively:

where ZnTE=ωμnβ, YnTM=ωɛnβ, ɛm′(u)=dduɛm(u), and φm′(u)=dduφm(u). Similar to Eq. (11), in Eqs. (12), (15), and (16), we utilize the tangential boundary conditions for the E_z-, E_φ-, H_z-, and H_φ-fields at ρ = b. Then, we formulate the modal relations of Em(1),(2),Fm(1),(2), G_m and H_m as

where v_n=κ_nb. Combining and simplifying Eqs. (11), (12), and (15)–(20), we obtained the mth hybrid-mode dispersion relation as

where |A| is the determinant of a matrix A and a system of simultaneous equations for Em(1),(2),Fm(1),(2) is given by:

The elements of Φ_m(β) are defined by:

where

Therefore, a complex propagation constant β can be determined by solving Eq. (21). When m = 0, the hybrid-mode dispersion relation shown in Eq. (21) can be divided into

Eq. (30) clearly proves that the TM and TE modes exist for m = 0, although the coaxial waveguide is filled with lossy dielectrics. Since Eq. (21) is applicable to a general coaxial waveguide of any μ_n and ε_n, we can use Eq. (21) to analyze canonical waveguides, including the PEC circular and coaxial waveguides. For instance, when μ_n = μ₀ and ε_n = ε₀, the geometry shown in Fig. 1 becomes a PEC circular waveguide with a radius of b + d, and Eq. (21) is thus simplified to

Similarly, when μ_n = μ₀, ε₁ → ∞, and ε₃ = ε₂, the geometry in Fig. 1 is considered a PEC coaxial waveguide. Then, the dispersion equation in Eq. (21) reduces to that of a PEC coaxial waveguide as

III. Numerical Computations

We used Davidenko’s method [10, 11] to search a complex root β by equating |Φ_m(β)| = 0 as shown in Eq. (21). Davidenko’s method in [11] uses the fourth-order Runge–Kutta method and the Newton–Raphson method in the complex domain, which is suitable for searching the complex propagation constant β. An iterative update equation for the next approximate solution β_n+1 is given by

where β_n is the current approximate value for β and Δβ_n+1 is defined in [11, Eq. (10)]. The next differential step Δβ_n+1 is computed using β_n, Δβ_n, and h, where β₀ and Δβ₀ are the initial value and step for root searching, respectively, and h is a fixed step of the Runge–Kutta method. As n increases very steeply, β_n+1 stably converges to β [10, 11]. We set h = 1 and Δβ₀ = β₀/100 for all root-searching computations.

The TM₀₁-mode dispersion results of the lossy coaxial waveguide are shown in Fig. 3 using m = 0 and f = 100 GHz, where the TM₀₁ mode (m = 0) is a dominant quasi-TEM mode. We assume that regions (I) and (III) are filled with lossy conductors using ɛ1=ɛ3=ɛ0 (1+iσωɛ0), where σ denotes the electrical conductivity of a lossy dielectric. Using Eq. (30) and the conductor condition (|ε₁| ≫ 1, |ε₃| ≫ 1), we obtain an approximate dispersion relation for the TM_0p mode as

Fig. 3

Complex dispersion relation versus electrical conductivity σ for the TM₀₁ mode in the lossy coaxial waveguide using m = 0, f = 100 GHz, 2a = 0.434 mm, 2b = 1 mm, μ_n = μ₀, ɛ1=ɛ3=ɛ0 (1+iσωɛ0), and ε₂ = ε₀: (a) phase constant ℜ[β] and (b) attenuation constant ℑ[β].

where P_n = ε₂κ_n/ε_nκ₂,

Note that setting U_m(v₂) and Vm′(v2) equal to zero yields the TM_mp- and TE_mp-mode dispersion relations of an ideal coaxial line, respectively, where the subscript mp means that m and p are the numbers of field variations in the φ- and ρ-directions, respectively. This property indicates that Eq. (34) is a perturbed but accurate solution for the lossy coaxial waveguide when P₁ and P₃ are very small owing to |ε₁| ≫ 1 and |ε₃| ≫ 1. Utilizing β ≈ k₂, |k₁| ≫ |β|, and |k₃| ≫ |β|, Eq. (34) can be further simplified to

when u → 0, N₀(u) and N0′(u) become 2πln (u2) and 2πu, respectively. Therefore, an approximate closed-form solution for Eq. (37) is finally obtained as

Note that Eq. (38) is identical to [7, Eq. (37)] even though the boundary conditions for the outer conductors are different from each other. When μ_n = μ₀ and σ ≫ 1, Eq. (38) becomes a complex propagation constant [5] obtained by the transmission line theory and penetration depth δ_s. Fig. 3 clearly indicates that the thickness (d) of an outer conductor hardly affects complex dispersion relations for σ ≥ 10³ S/m and d ≥ 0.2 mm ≈4δ_s, where δ_s ≈ 50 μm and σ = 10³ S/m. A comparison with [8] provides a favorable agreement when σ ≥ 10³ S/m. This is because [8] assumes an infinite outer conductor (d → ∞) and the effects of the thick outer conductor are negligible for high electrical conductivity, where the outer conductor shown in Fig. 1 has finite thickness (d), which differs from [8]. As is also shown in Fig. 3, Eqs. (34) and (38) are practically good formulas in lieu of Eq. (21) for σ ≥ 10³ S/m. When σ approaches zero, Eq. (31) predicts that β becomes that of a PEC circular waveguide denoted as ○ in Fig. 3. The insets in Fig. 3 illustrate the normalized real and imaginary parts of the E_z-field distributions when σ = 10⁴ S/m and β ≈ 2161.77+65.96i rad/m. The real and imaginary E_z-fields of the TM₀₁ mode are continuous across the boundaries at ρ = a and b, thus verifying that Davidenko’s method in Eq. (33) is effective for searching the complex root β of a lossy coaxial waveguide. In addition, the magnitude of the E_z-fields is rapidly attenuated within lossy dielectrics in regions (I) and (III), and thus their field distributions illustrate the behaviors of the penetration depth very well.

Fig. 4 shows the dispersion behaviors of the TM₀₁, TE₀₁, and EH₁₁ modes in the lossy coaxial waveguide versus microwave frequency. The TM₀₁ mode has the lowest attenuation when compared with the TE₀₁ and EH₁₁ modes, thus indicating that the TM₀₁ mode is a dominant mode irrespective of σ. Applying Eq. (30) and the conductor condition (|ε₁| ≫ 1, |ε₃| ≫ 1) yields an approximate dispersion equation for the TE_0p mode as

Fig. 4

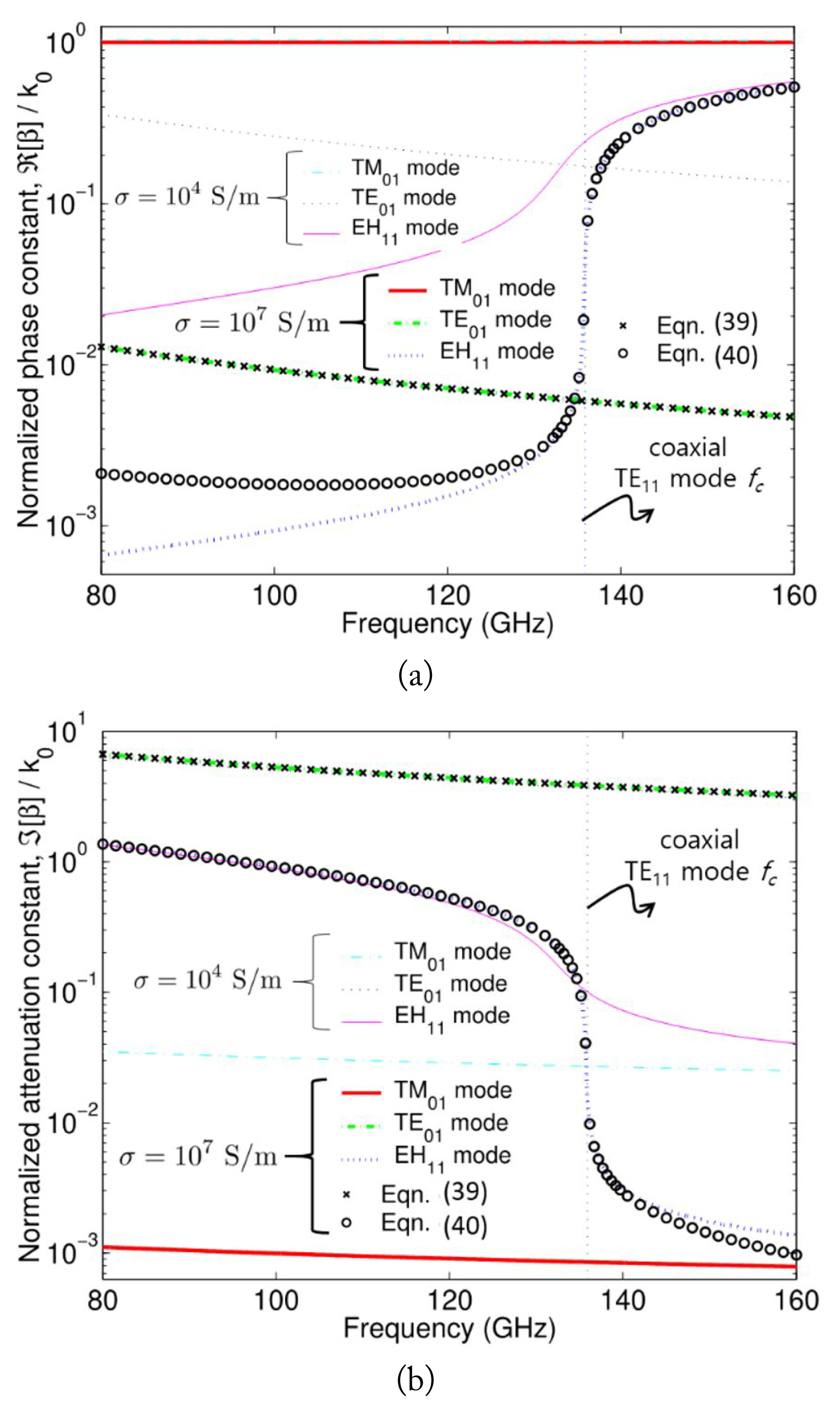
Microwave behaviors of complex dispersion relations of multiple modes in the lossy coaxial waveguide using m = 0 or 1, d = 0.4 mm, and the same parameters given in the caption of Fig. 3. The coaxial TE₁₁-mode cutoff frequency (f_c) is computed using an ideal coaxial line: (a) phase constant ℜ[β] and (b) attenuation constant ℑ[β].

where Q_n = μ_nκ₂/μ₂κ_n. Similar to Eqs. (34) and (39), the dispersion relation Eq. (21) approximately reduces to

When σ ≥ 10⁷ S/m, the magnitude of ε₁ and ε₃ becomes very high and thus the TE₀₁- and EH₁₁-mode β computed by Eqs. (39) and (40) agree well with more precise solutions obtained by Eqs. (30) and (21), respectively. In Fig. 4, the attenuation constant (ℑ[β]) of the EH₁₁ mode rapidly decreases above f_c ≈ 135.9 GHz. Therefore, the TM₀₁ and EH₁₁ modes coexist and propagate along the lossy coaxial waveguide above f_c. Considering Eq. (40), the cutoff frequency (f_c) of the lossy EH₁₁ mode can be approximately determined using V1′(v2)≈0, which is related to f_c of the TE₁₁ mode in an ideal coaxial line. The vertical dotted lines as shown in Fig. 4 denote f_c of the coaxial TE₁₁ mode.

Fig. 5 illustrates the dispersion characteristics of the TM₀₁ and EH₁₁ modes within the visible spectrum. To theoretically obtain the dispersion relations of the lossy coaxial wave-guide composed of real metals, we use optical dielectric constants [12] of silver (Ag), copper (Cu), and gold (Au). In the visible spectrum, the real part of the metal permittivity is usually negative caused by plasma oscillation in the metal. Fig. 5 indicates that Eq. (38) is valid within the optical spectrum and the cutoff or transition wavelength (λ_c) can be obtained by Eq. (40). As a result, our approximate solutions obtained from Eqs. (38) and (40) are useful for predicting the optical behaviors of the TM₀₁ and EH₁₁ modes in the nanoscale coaxial waveguide.

Fig. 5

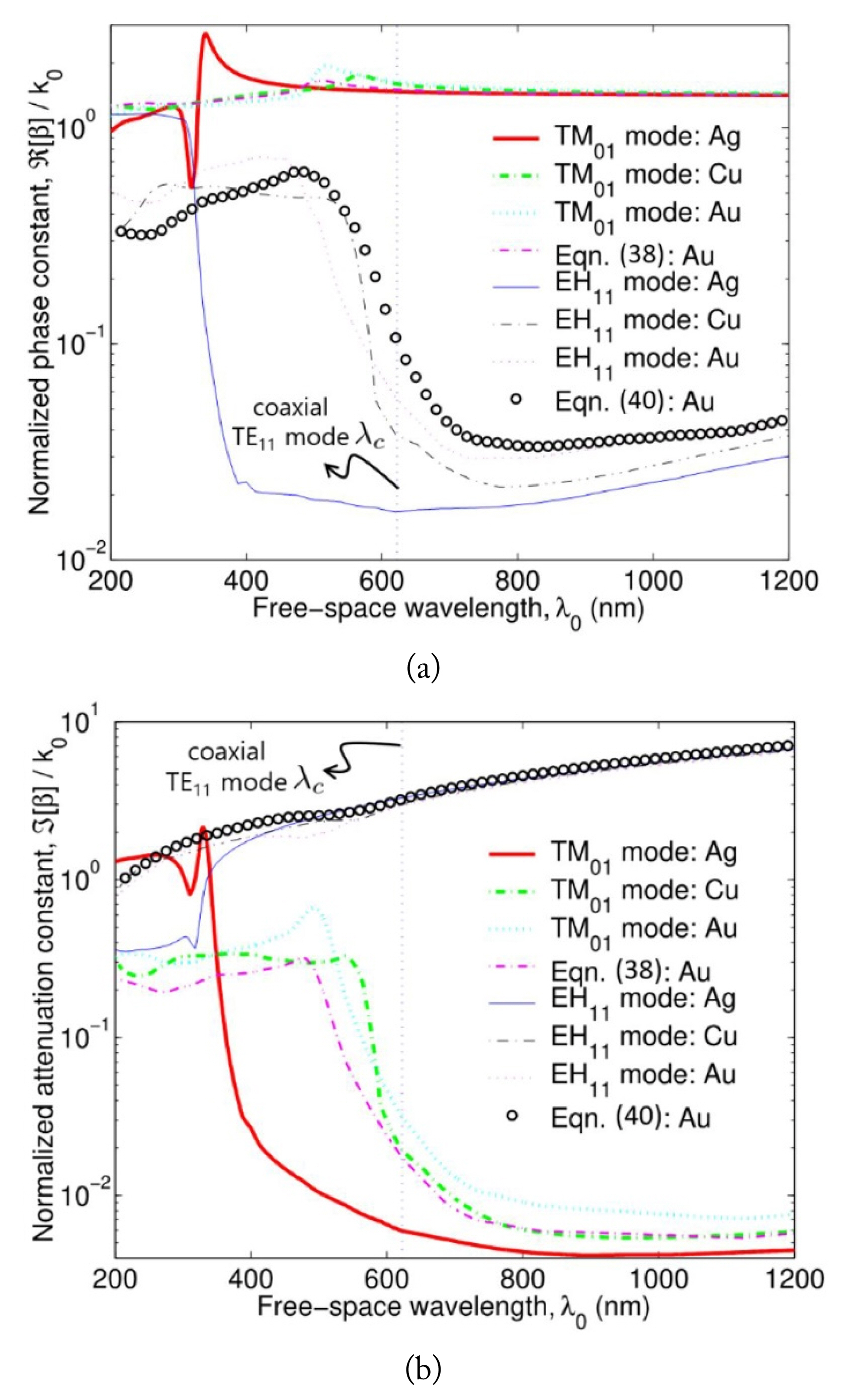
Optical behaviors of complex dispersion relations of silver (Ag), copper (Cu), and gold (Au) coaxial waveguides using m = 0 or 1, a = 75 nm, b = 125 nm, and d = 100 nm, μ_n = μ₀, ε₂ = ε₀, and ε₁ and ε₃ (ε₁ = ε₃) are determined by optical dielectric constants of metals: (a) phase constant ℜ[β] and (b) attenuation constant ℑ[β].

IV. Conclusion

Analytical hybrid-mode dispersion relations of the lossy coaxial waveguide are presented based on the mode-matching technique and the vector potential formulations. Precise phase and attenuation constants of the TM₀₁, TE₀₁, and EH₁₁ modes have been numerically evaluated using the root-searching algorithm based on Davidenko’s method. Approximate but accurate dispersion equations for the TM_0p, TE_0p, EH_mp, and HE_mp modes are also proposed and agree well with more rigorous dispersion relations even for low electric conductivity or negative permittivity. Our dispersion solutions can be applied to the theoretical evaluation of a coaxial calibration kit or the analytical determination of light distribution within the optical coaxial waveguide.

Article information Continued