|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 21(4); 2021 > Article |
|
Abstract
In this paper, a two-coil magnetic resonance wireless transmission system is studied to improve the transmission distance using transformers. A conventional two-coil and four-coil wireless power transmission (WPT) system as well as a two-coil WPT system with transformers are analyzed comparatively via circuit simulations and experiments. Circuit analysis was used to predict the transmission distance with the highest efficiency. To verify the improvement in the transmission distance of the proposed system, transformers with inductance values of 80, 100, and 140 ╬╝H were fabricated and analyzed through experiments and simulations. A maximum S21 parameter of 0.76 was noted when the inductance was 80 ╬╝H and the transmitting distance was 4 cm. The experimental results almost matched the simulation results. From the experiments, it was shown that the transmitting distance of a WPT system can be adjusted by using transformers. Additionally, it was found that the transmitting distance is inversely proportional to the transformer inductance, and the efficiency of the WPT system decreases with the transmitting distance.
Wireless power transmission (WPT) is a promising technology used in charging electric devices such as mobile phones, tablet, and electric vehicles [1ŌĆō3]. Two-types of WPT technology have been studied: a magnetic resonance method and an inductive coupling method [4]. Inductively coupled WPT has already been used in the industry. Moreover, the short transmission distance of inductively coupled WPT limits its applications. However, magnetic resonance WPT transmits farther than inductively coupled WPT, and this had led to magnetic resonance WPT being used widely in various applications [5, 6].
The magnetic resonance between resonance coils allows for power transmission from a few centimeters to a few meters. The impedance matching of the transmission and receiving coils allows for farther power transmission. Depending on the system, three or four coils are used in magnetic resonance WPT [7ŌĆō9]. The magnetic resonance method has a specific transmitting distance with a high transmitting efficiency. The specific distance increases as the impedance of the source and the load is small while that of the transmitting and receiving coils is large. The disadvantages of magnetic resonance WPT include the difficulty involved in the impedance matching and the large volume of the system [10].
In this paper, a two-coil WPT system with transformers is studied to improve the transmission distance and reduce the system volume of the conventional WPT system. The conventional four-coil WPT system needs to be designed considering three coupling coefficients between the coils. However, the proposed system makes the impedance matching simpler by using a fixed coupling coefficient for the transformers, which is nearly 1 and the coupling coefficient between the transmitting and receiving coil.
To verify the proposed WPT, both the conventional and proposed WPT are analyzed comparatively through simulations and experiments. The magnetically coupled circuit model of the proposed WPT is simulated and analyzed using passive circuital elements. The circuit model is used in estimating the optimum transmitting distance with a maximum transferring efficiency. The proposed WPT is also studied by varying the inductance of the transformers to observe the change in the transmitting distance.
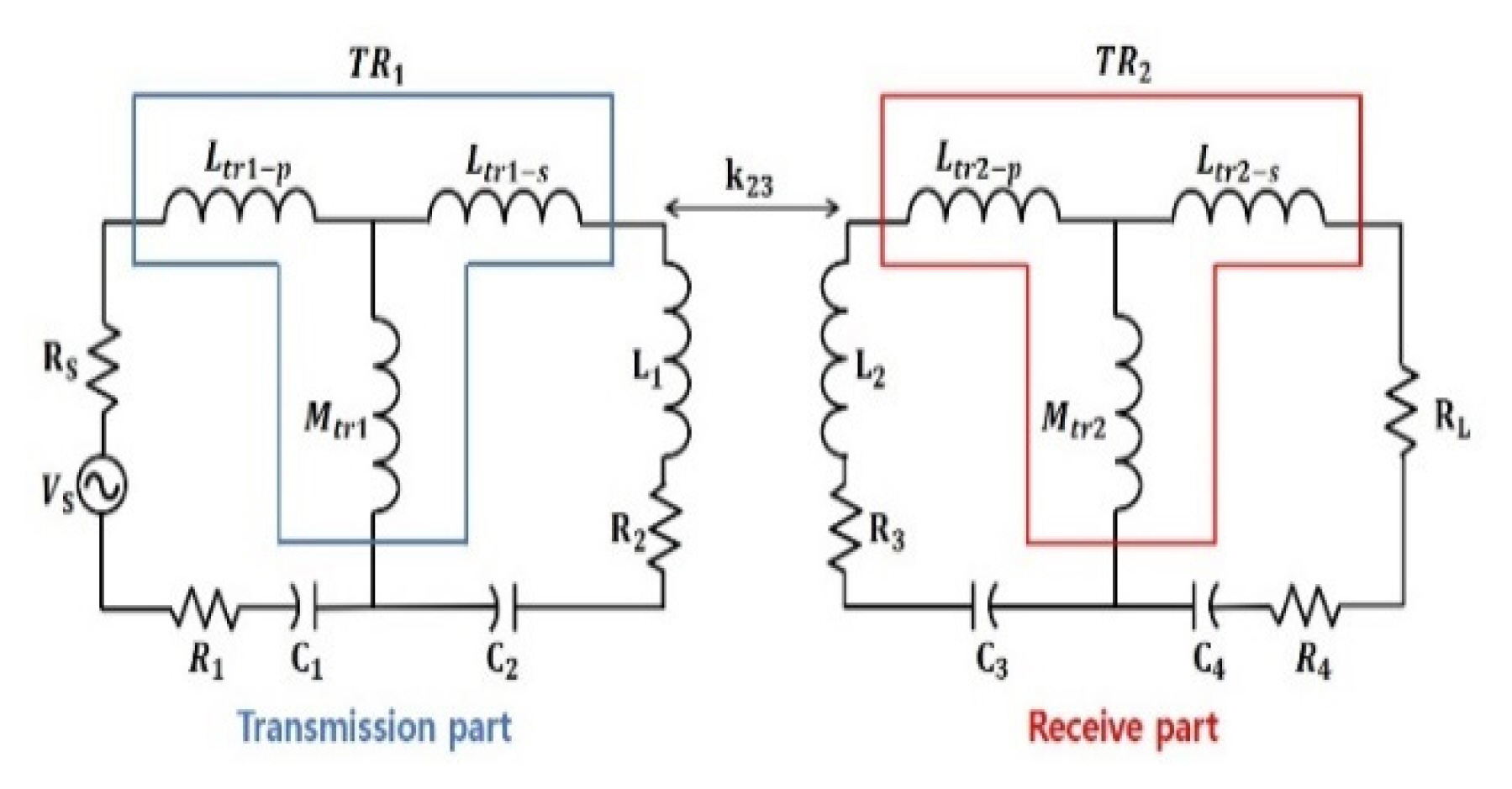
Fig. 1 shows a schematic circuit of the two-coil magnetic resonance WPT system with transformers. The circuit is composed of the voltage source (Vs), the source resistance (Rs), the load resistance (RL), and capacitors for resonance (C1, C2, C3, C4). Helical coils were used as the transmitting (Tx) and receiving (Rx) coils. When an electric power with the same resonance frequency as the LC circuit is applied to the transformers (TR1, TR2), a magnetic field is generated from the transmitting coil. The generated magnetic field transmits electric power to the receiving coil. Then the receiving part of the coil operates analogous to the transmitting part. The receiving part of the coil is modeled by substituting the power source of the transmitting part to the load.
The impedance matching circuit of the transmitting and receiving coils allows for mid-distance WPT. The transformer used in the proposed system provides impedance matching in the circuit.
By assuming that the loss from the inner resistance of the coil is neglected, it can also be assumed that the energy not transferred to the receiving coil remains in the transmitting coil at the resonance frequency. Therefore, the matched coils increase the transferring efficiency even though the mutual inductance is extremely small [11]. Although it has two coils, the proposed two-coil system has characteristics similar to the four-coil system and not the conventional two-coil system. The RLC circuit, sharing a mutual inductance, has a high transferring efficiency at frequencies higher and lower than the resonance frequency.
This phenomenon is called the frequency split, which converges to the resonance frequency as the mutual inductance of the coils decreases. The frequency split is a feature of mid-distance WPT and not observed in two-coil WPT [12].
The circuit model of the proposed WPT system is shown in Fig. 2; it is used in the circuit simulation and can be analyzed numerically.
The circuit model of the proposed WPT system is composed of two T-equivalent circuits. The resonance circuit is represented as a RLC circuit using lumped elements. The four-resonance circuit is magnetically coupled using transformers as well as the transmitting and receiving coils. Mtr1 and Mtr2 are the mutual inductances of transformers 1 and 2, respectively. The coupling coefficient of the transmitting and receiving coils is k23.
The first part of the transmitting circuit is composed of the power source (Vs), source impedance (Rs), primary leakage inductance of the transformer 1 (Ltr1-p), and internal resistance of transformer 1 (R1). The second part of the transmitting circuit is composed of the secondary leakage inductance of transformer 1 (Ltr1-s), the inductance of the transmitting coil (L1), and the composite resistance of the internal resistance of the transformer and the coil resistance (R2).
The capacitors are connected in a series to the first and second part of the transmitting circuit. The capacitance, C1, is determined by the sum of the primary leakage inductance (Ltr1-p) and mutual inductance (Mtr1). The capacitance, C2, is determined by sum of the secondary leakage inductance (Ltr1-s), mutual inductance (Mtr1), and inductance of the transmitting coil (L1). The receiving circuit is composed similarly to the transmitting circuit.
Eq. (1) is represented using KirchhoffŌĆÖs voltage law (KVL) to analyze the proposed WPT system. The current of each resonance circuit is calculated using KVL. The mutual inductance in Eq. (1) is substituted with the coupling coefficient using Eq. (2). Eq. (4), which is a power transfer function, (
V L V s
The WPT system is considered a two-port network. The S21 parameter is calculated using Eq. (4) and is represented in Eq. (5) [14]. (S21)2 represents the maximum power ratio and transferring efficiency of the WPT.
Fig. 3 shows the transfer function of the proposed WPT system depending on the change in the coupling coefficient (k23) and frequency. The red-colored area represents a highly efficient operation. The figure shows a frequency split, a characteristic of a mid-distance WPT system. The values of the circuit elements used in calculating the transfer function are listed in Table 1.
Moreover, kcritical represents the specific distance for high-efficiency operation when the system is in its resonance [12]. When k23 is larger than kcritical, the WPT system is over-coupled and has two frequencies with a high efficiency. As the coupling coefficient decreases, the frequency for a high S21 converges to the critical point. When k23 is smaller than kcritical, the transferred power decreases rapidly with distance.
Unlike conventional two-coil WPT, the proposed WPT shows a frequency split and is capable of mid-distance power transmission. The calculation of an optimum kcritical is necessary for efficient power transmission and is described in the next section.
Using Eq. (4)kcritical, which provides a high transmission efficiency to the proposed WPT system, can be deduced. When the system is in resonance, the system impedance is represented as Eq. (6).
To simplify the equations, the inductance is substituted into the Q-factor. Eq. (7) represents the relationship between the inductance and Q-factor.
In Eq. (8), the Q-factor with the same inductance is organized to have the same value; Qtr1-p = Qtr2-p = QP, Qtr1-s = Qtr2-s = QS, and Q1 = Q2 = Qcoil. Because the coupling coefficient of the transformer is approximately 1, the coupling coefficient is substituted to ktr1 = ktr2 Ōēł1. The modified equation is given as \Eq. (9). Under resonance, the voltage gain in Eq. (9) is the same as in Eq. (3).
The critical coupling coefficient, kcritical, can be derived by differentiating Eq. (9). kcritical in Eq. (10) represents k23 at which the transmitting and receiving coil transmits maximum power. The distance between the coils is inversely proportional to k23.
According to Eq. (10), a small kcritical is attained when the inductance of the transformer is small, and the inductances of the transmitting and receiving coils are large. Fig. 4 shows the change in kcritical when the inductances of the transmitting and receiving coils are fixed, and the transformer inductance is 80, 110, and 140 ╬╝H. Depending on the transformerŌĆÖs inductor, the red part of Fig. 4, which represents a high-efficient operation, varies. Although the transmitting distance is lengthened, when the transformerŌĆÖs inductance decreases, the transmitting efficiency is reduced due to the reduced kcritical. The values of the circuit elements used in the calculation is shown in Table 1. The transformerŌĆÖs inductance and capacitance are calculated based on the resonance frequency.
The proposed two-coil WPT system and conventional two-coil and four-coil WPT systems were studied through experiments. Fig. 5 shows the experimental system. The two-coil WPT system consists of transmitting and receiving coils as well as capacitors (C2, C3) [4]. The four-coil system consists of a two-coil system with the addition of a source coil and a load coil. In the four-coil system, the capacitors are connected in a series to compensate for the coil inductances [13]. The transmitting and receiving coils (with a diameter of 170 mm) are wound using a 0.05 mm enameled wire. The capacitance for the resonance operation is calculated using Eq. (7). The two-coil WPT system with transformers consists of a source transformer, transmitting and receiving coils, and a load transformer. Transformers with a ferrite core, which have a high permeability and high magnetic flux density, are used in the proposed WPT system to minimize the losses due to the frequency. To minimize the system volume, a PQ-type core is used in the transformers, which are wound using the same enameled wire used in the transmitting and receiving coils.
The three WPT systems were operated using a function generator, and the voltage and current were measured using the Tektronix DPO3054. The WPT systems were operated at 60 kHz, which is one of the frequencies available for high-power WPT systems enacted by the International Telecommunication Union (ITU). The system can operate at different frequencies when the resonant frequency of the transformers and the transmitting and receiving coils are the same. An acrylic structure is used to support the coils and adjust the distance between the coils. The distance between the coils is altered from 0 to 15 cm in 1 cm steps. Through the experiments, an average S21 parameter was measured. The values of the circuit elements used in the simulation and experiments are shown in Table 2.
Although the transmitting distance is slightly shorter than that of the four-coil system, the experiments show that the proposed WPT system lengthens the transmitting distance compared to the conventional two-coil WPT system. The maximum S21 parameter for the proposed system is 0.76 at a coil distance of 4 cm. The maximum S21 parameter for the conventional two-coil and four-coil system is 0.93 at a coil distance of 0 cm and 0.79 at a coil distance of 6 cm, respectively. The results are shown in Fig. 6.
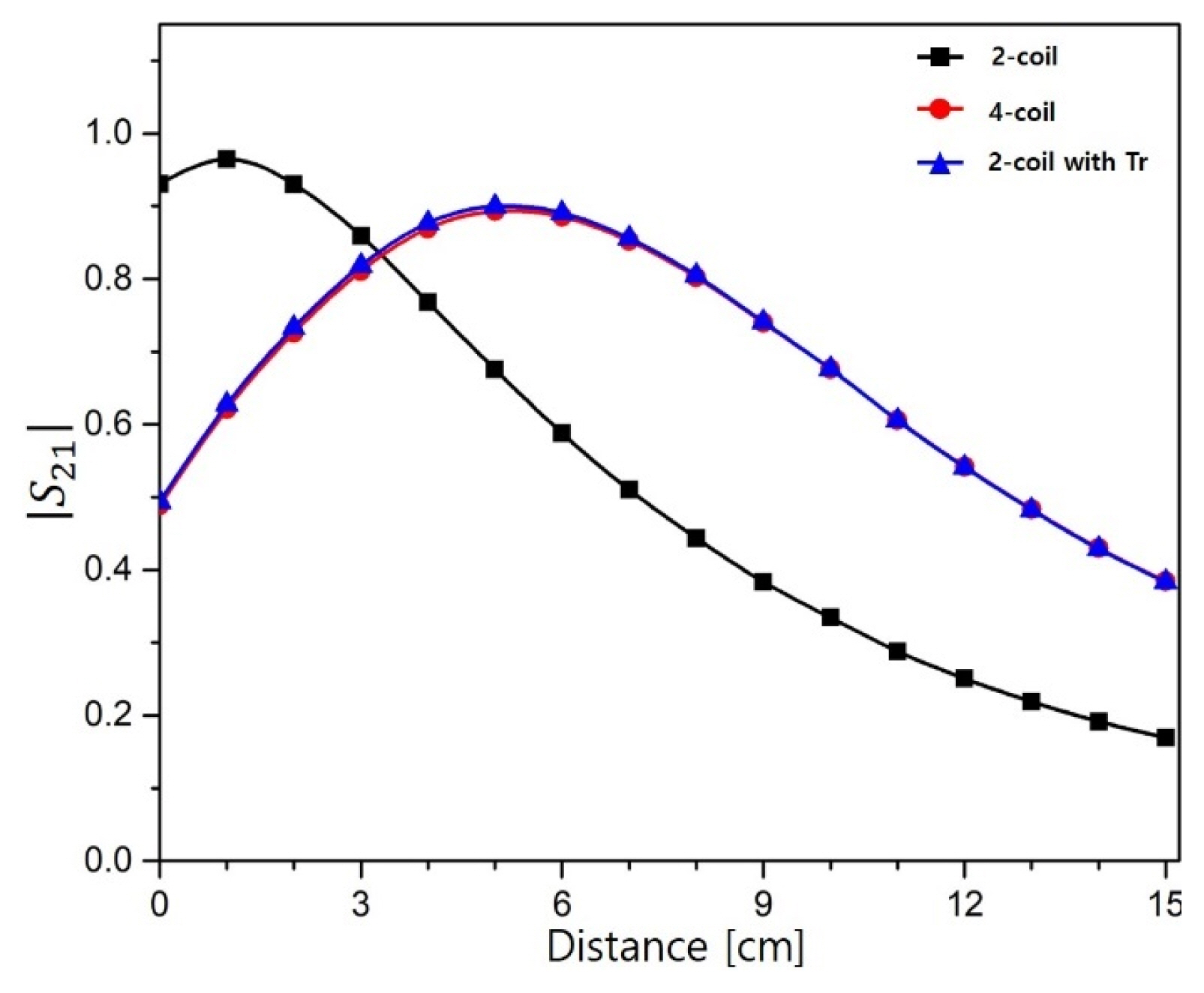
According to the simulations, the maximum S21 parameter of the proposed WPT system and the conventional two-coil system and four-coil system is 0.9 at 5 cm, 0.93 at 1 cm, and 0.89 at 5 cm, respectively. The simulation results are shown in Fig. 7. The maximum S21 of both the conventional two-coil system and proposed system is 1 cm shorter compared to that in the simulation. However, the maximum S21 of the four-coil system is 1 cm farther compared to that of the simulation. Additionally, the experimental efficiency was measured as less than that of the simulation when the transmitting distance was greater. The difference between the experiment and the simulation results is presumed to be the measuring error of the inductance and capacitance.
Transformers with inductance values of 80, 110, and 140 ╬╝H were fabricated to analyze the change in kcritical with the change in the transformer inductance. The three types of transformers were analyzed using the same transmitting and receiving coils.
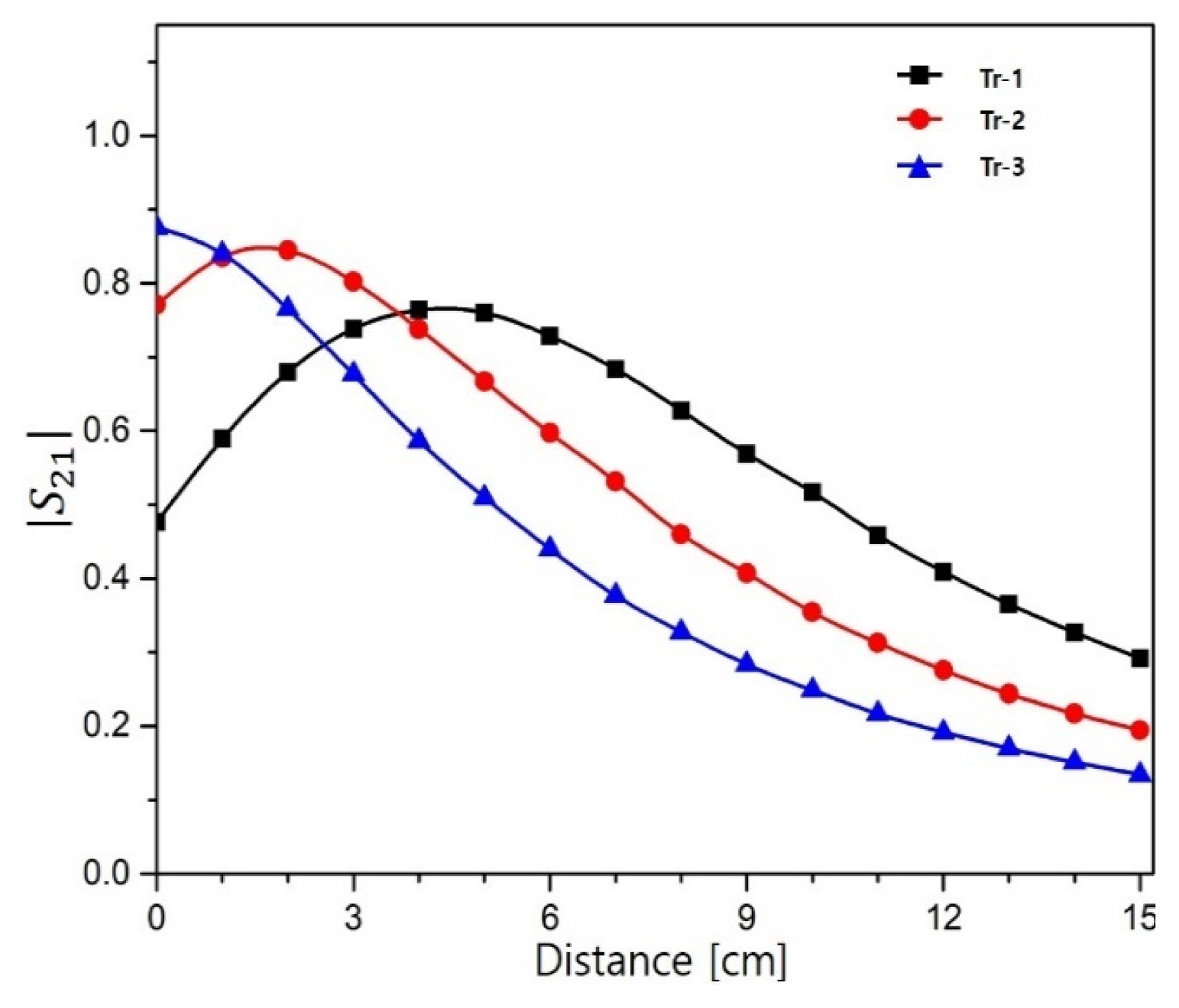
From the experiments, it is shown that kcritical varies with the change in the transformer inductance. Fig. 8 shows the change in the S21 parameter with the transformer inductance. The maximum S21 for the transformer with 80 ╬╝H (Tr-1) is 0.76 at 4 cm. The maximum S21 for the transformer with 140 ╬╝H (Tr-3) is 0.87 at 0 cm.
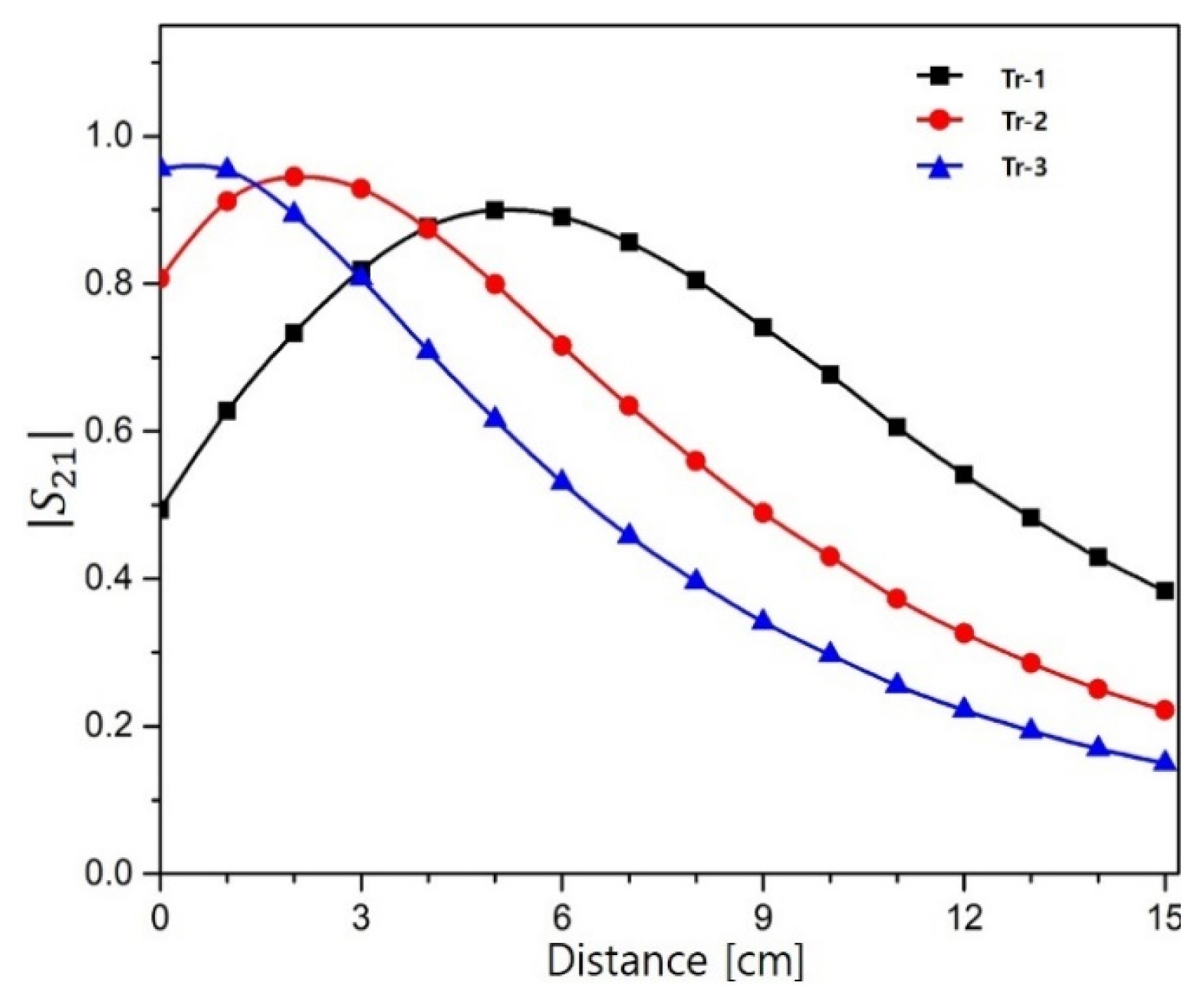
Fig. 9 shows the simulation results. According to the simulation, the maximum S21 for the transformer with 80 ╬╝H is 0.9 at 5 cm. The maximum S21 for the transformer with 140 ╬╝H is 0.95 at 0 cm.
Although the kcritical and S21 values were mostly the same, S21 demonstrated a greater difference between the experiments and simulations. This difference tended to increase with the transmission distance. Due to the operation frequency limits of the transformer, the proposed system is operated at a lower frequency compared to the conventional magnetic resonant WPT system. The lower operating frequency and radiation losses are considered to be the cause of these differences.
A two-coil WPT system with transformers was studied in this paper to increase the short transmission distance. According to the simulations and experiments, it was shown that the proposed WPT system transmits electric power farther than the conventional two-coil WPT system and has similar operating features as the four-coil WPT system. The system parameter was analyzed to find kcritical, thereby giving a high efficiency to the proposed WPT. The system parameter for the optimum distance could be found from the experiments. kcritical decreases as the transformer inductance decreases, and the decrease in kcritical leads to an increased transmission distance. Transformers with different inductances were used in the experiments and simulations to verify the hypothesis. A maximum S21 of 0.84 at 2 cm and 0. 76 at 4 cm were obtained with inductance values of 110 ╬╝H and 80 ╬╝H, respectively. Despite some slight errors, the simulations and experiments can be considered as having agreement with the results. These results will be studied in future work to obtain a WPT system with constant power transferring efficiencies regardless of the change in the transmitting distance.
Fig.┬Ā3
S21 graph based on the frequency of the two-coil WPT system with transformers and the coupling coefficient of the transmitting and receiving coil.
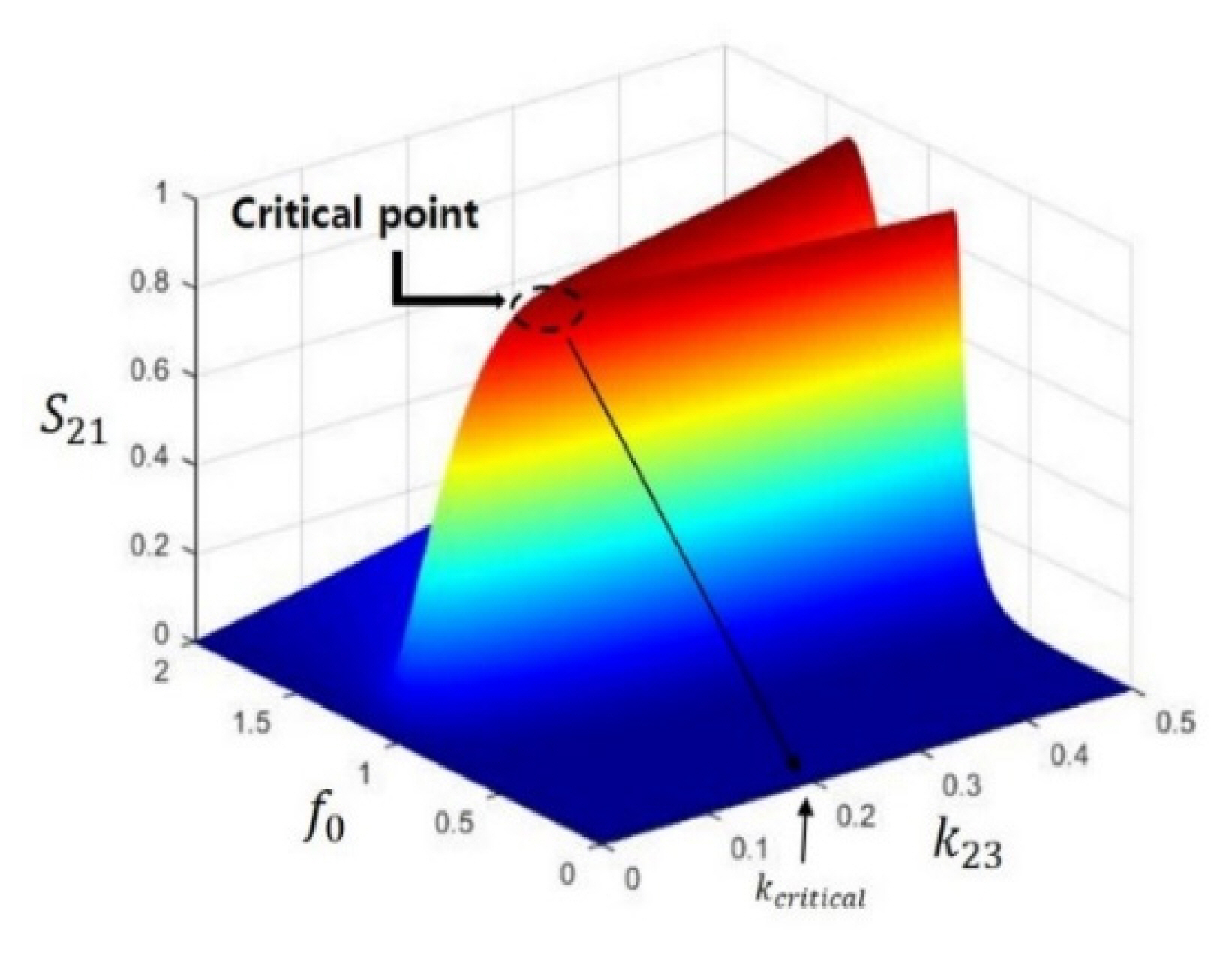
Fig.┬Ā4
The change in kcritical depending on the inductance of the transformers used in the proposed WPT system: (a) 80 ╬╝H, (b) 110 ╬╝H, and (c) 140 ╬╝H.
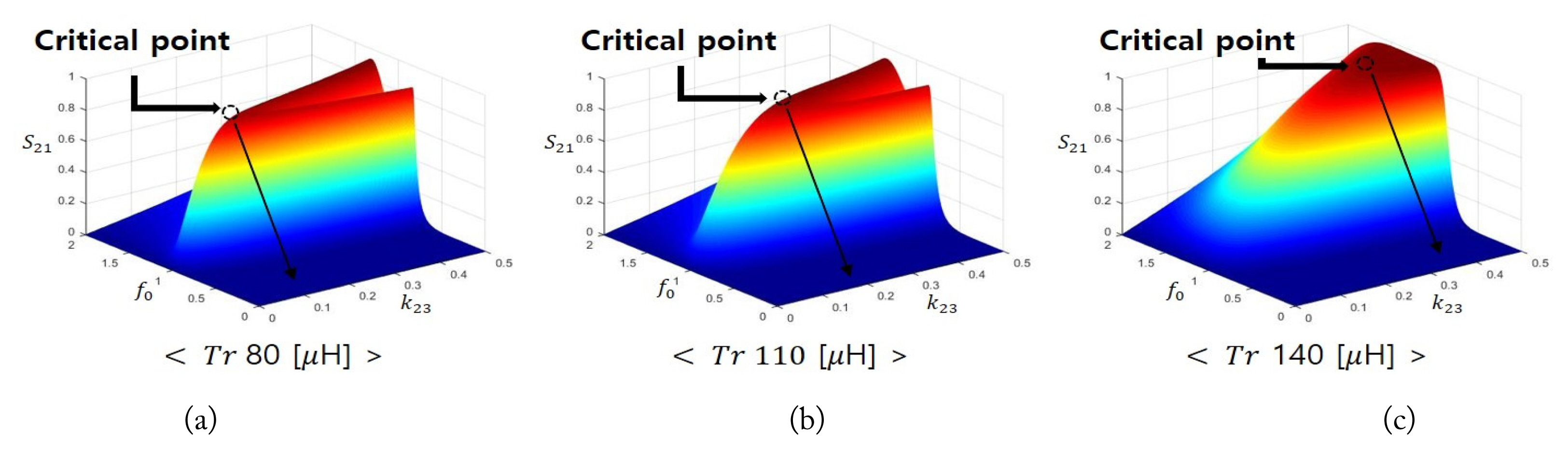
Fig.┬Ā6
Experimental results of the conventional two-coil and four-coil WPT system as well as the two-coil WPT system with transformers (Tr).
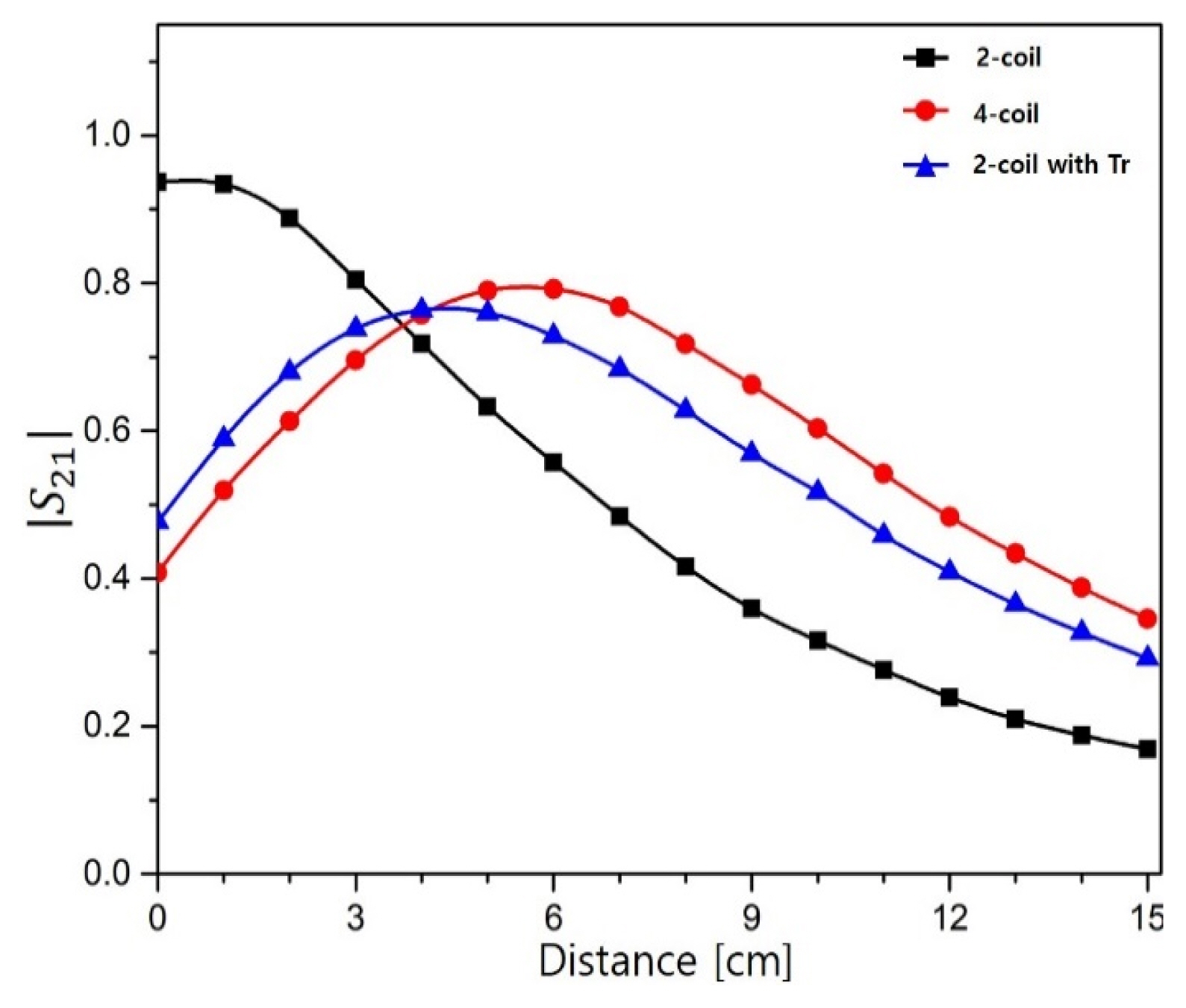
Fig.┬Ā7
Simulation results of the conventional two-coil and four-coil WPT system, and the two-coil WPT system with transformers (Tr).
Table┬Ā1
Circuit element values used in calculating the S21 graph
Table┬Ā2
Value of the circuit elements used in the conventional two-coil and four-coil WPT system as well as the proposed two-coil WPT system
References
1. J Hur and H Choo, "Design of a small array antenna with an extended cavity structure for wireless power transmission," Journal of Electromagnetic Engineering and Science, vol. 20, no. 1, pp. 9ŌĆō15, 2020.

2. G Kim, S Boo, S Kim, and B Lee, "Control of power distribution for multiple receivers in SIMO wireless power transfer system," Journal of Electromagnetic Engineering and Science, vol. 18, no. 4, pp. 221ŌĆō230, 2018.

3. S Kim, S Hwang, S Kim, and B Lee, "Investigation of single-input multiple-output wireless power transfer systems based on optimization of receiver loads for maximum efficiencies," Journal of Electromagnetic Engineering and Science, vol. 18, no. 3, pp. 145ŌĆō153, 2018.

4. T Imura and Y Hori, "Maximizing air gap and efficiency of magnetic resonant coupling for wireless power transfer using equivalent circuit and Neumann formula," IEEE Transactions on Industrial Electronics, vol. 58, no. 10, pp. 4746ŌĆō4752, 2011.

5. A Kurs, A Karalis, R Moffatt, JD Joannopoulos, P Fisher, and M Soljacic, "Wireless power transfer via strongly coupled magnetic resonances," Science, vol. 317, no. 5834, pp. 83ŌĆō86, 2007.


6. H Lee, S Boo, G Kim, and B Lee, "Optimization of excitation magnitudes and phases for maximum efficiencies in a MISO wireless power transfer system," Journal of Electromagnetic Engineering and Science, vol. 20, no. 1, pp. 16ŌĆō22, 2020.

7. M Kiani, UM Jow, and M Ghovanloo, "Design and optimization of a 3-coil inductive link for efficient wireless power transmission," IEEE Transactions on Biomedical Circuits and Systems, vol. 5, no. 6, pp. 579ŌĆō591, 2011.

8. CK Lee, WX Zhong, and SYR Hui, "Effects of magnetic coupling of nonadjacent resonators on wireless power domino-resonator systems," IEEE Transactions on Power Electronics, vol. 27, no. 4, pp. 1905ŌĆō1916, 2011.

9. T Sun, X Xie, G Li, Y Gu, Y Deng, and Z Wang, "A two-hop wireless power transfer system with an efficiency-enhanced power receiver for motion-free capsule endoscopy inspection," IEEE Transactions on Biomedical Engineering, vol. 59, no. 11, pp. 3247ŌĆō3254, 2012.


10. W Huang and H Ku, "Analysis and optimization of wireless power transfer efficiency considering the tilt angle of a coil," Journal of Electromagnetic Engineering and Science, vol. 18, no. 1, pp. 13ŌĆō19, 2018.

11. L Chen, S Liu, YC Zhou, and TJ Cui, "An optimizable circuit structure for high-efficiency wireless power transfer," IEEE Transactions on Industrial Electronics, vol. 60, no. 1, pp. 339ŌĆō349, 2011.

12. G Lee and WS Park, "Analysis and comparison for a 4-coil magnetic resonance wireless power transfer system," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 24, no. 2, pp. 168ŌĆō179, 2013.

13. AP Sample, DT Meyer, and JR Smith, "Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer," IEEE Transactions on Industrial Electronics, vol. 58, no. 2, pp. 544ŌĆō554, 2010.

14. R Mongia, IJ Bahl, P Bhartia, and J Hong, RF and Microwave Coupled-Line Circuits. Norwood, MA: Artech House, 2007.
Biography

Chang-Jin Lee received a B.S. degree in Electrophysics from Hallym University, Chuncheon, Korea in 2015. He is currently pursuing a Ph.D. degree with the Applied High Power Engineering Laboratory at the Department of Electrical Engineering of the Hanyang University. His current research interests include wireless power transfer and its applications.
Biography

Se-Hoon Kim received a B.S. degree in Electrical Engineering from Hanyang University, Seoul, Korea in 2015. He is currently working toward his Ph.D. degree with the Applied High Power Engineering Laboratory at the Department of Electrical Engineering of the same university. His current research interests include the compact pulsed-power system, the high-power microwave system, and their applications.
Biography

Wan-Il Kim received a B.S. degree in Electrical Engineering from Hankyong University, Korea, in 2016, and then received a M.S. degree from Korea National University of Transportation in 2018. He is currently pursuing a Ph.D degree with the Department of Electrical Engineering of Hanyang University, Korea.
Biography

Kwang-Cheol Ko received his B.S. degree in Electrical Engineering from Hanyang University, Seoul, Korea in 1982, and M.S. and Ph.D. degrees from the Tokyo Institute of Technology, Tokyo, Japan in 1986 and 1989, respectively. From 1990 to 1995, he was an Assistant Professor with the Department of Electrical Engineering, Kyungwon University, Seongnam, South Korea. In 1995, he joined the faculty of the Department of Electrical Engineering, Hanyang University, where he is currently a professor. His current research interests include pulsed-power technologies and their applications.
- TOOLS
-
METRICS

-
- 1 Crossref
- 0 Scopus
- 2,546 View
- 78 Download
- Related articles in JEES
-
Magnetic Resonance-Based Wireless Power Transmission through Concrete Structures2015 ;15(2)
Analysis of Magnetically Coupled Wireless Power Transmission for Maximum Efficiency2011 ;11(3)
Analysis of a Linkage Coil for Wireless Power Transmission by Inductive Coupling2008 ;8(1)