I. Introduction
The fifth-generation (5G) network has been being rolled out and has exhibited a remarkable performance, such as a higher data rate, larger network capacity, lower latency, and ubiquitous mobile coverage, compared to its predecessors [
1]; however, the exponential growth in data usage demand and the number of wireless devices creates new challenges for the 5G network as well as the next-generation networks [
2]; especially, in the era of Internet of Things (IoT), this problem becomes more critical. Numerous technical efforts have been done for enlarging the network’s capability and enhancing the quality of service toward advanced communication applications. For instance, massive multiple-input-multiple-output (MIMO) technology, which uses a large number of antennas to achieve higher coverage and capacity, was introduced. A large millimeter-wave (mmWave) spectrum band is exploited to allow high-speed connectives and high network capacity. Moreover, non-orthogonal multiple access (NOMA), which uses a power-domain multiplexing technique to accommodate several users within an orthogonal resource block, showed a significant improvement in spectrum efficiency [
3].
Recently, the intelligent reflecting surface (IRS), which is capable of reflecting electromagnetic waves with a controllable phase-shift and direction, has emerged as a promising technique to realize a smart and programmable wireless environment [
4]. The key idea of the IRS is based on special electromagnetic properties on repetitive artificial subwavelength structures [
5]. For convenience in manufacturing and deployment, the IRS consists of a large number of independent reflecting tiles (RTs) that are interconnected and controlled by a programmable controller. To verify the advantages of the IRS, the performance of IRS-aided wireless systems has been studied. The works on IRS’s physical channel modeling and channel estimation were done in [
6–
8], allowing for a performance evaluation of IRS-aided communication systems. In [
9–
12], the authors proposed potential applications of the IRS in various communication systems, such as wireless powered networks, secure communications, terahertz communications, cognitive radio systems, and MIMO systems, and showed that these systems gain a significant improvement in performance.
In this paper, we study the advantages of the IRS on enhancing performance of a practical indoor NOMA communication with imperfect successive-interference-cancellation (SIC) and in the presence of phase distortion (PD) caused by a non-ideal IRS. Unlike other approaches, where extravagant state variations are required at the IRS, our approach evaluates average performance metrics, i.e., the average achievable rates (AARs) at users, to significantly reduce IRS’s state variations, hence achieving robust power efficiency. First, we adopt a novel channel model proposed for indoor IRS-aided wireless communications in [
10] to derive the signal-to-interference-plus-noise ratios (SINRs) for each signal at each user. Next, we study the distribution characterization of relevant performance metrics. Finally, the theoretical AAR formulas can be obtained using the above results. Numerical results are presented for analysis verification and performance evaluation. Moreover, these results point out the effects of system parameters, such as source transmit power, NOMA power allocation (PA) factors, RT allocation, the PD factor, and the SIC imperfection factor, on system performance.
The rest of this paper is organized as follows. The system and channel models are described in Section II. The SINR’s distribution and theoretical AAR formulas are studied in Section III. Numerical results and discussions are presented in Section IV. Finally, conclusions are presented in Section V.
Notation
Rice(Ω,
K) denotes the Rice distribution with scale parameter Ω and shape parameter
K;
CN(0,
δ2) denotes the complex Gaussian distribution with zero mean and variance
δ2;
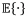
is the expectation of a random variable (RV)
X.
II. System and Channel Models
We consider an IRS-aided NOMA communication, as illustrated in
Fig. 1, in which a source
S communicates with two users, a near user
U1 and a far user
U2, with the help of an IRS attached to a wall. All nodes are single-antenna devices. The NOMA technique is used for data transmission for the users. The IRS includes
N RTs,
Rn,
n = 1,…,
N, and each RT is a reconfigurable metasurface and can independently direct the signal to a user under the control of a programmable controller. The channel model proposed for indoor IRS-aided wireless communications in [
10,
13] is adopted to characterize the wireless channels of our system. For instance, the received signal at
Um,
m ∈ 1, 2, comprises of (i) the signals propagating over the line-of-sight (LoS) (or the direct link) and reflecting links, both are the dominant links, and (ii) scattering signals caused by multi-path fading or multiple reflections on the IRS. Let ℛ
m be the set of RTs allocated to
Um,
m = {1, 2}; hence, the channel between
S and
Um is expressed as
where
hmLoS and
hSRnUmRef are channel coefficients for the LoS link between S and Um and for the reflecting link between S and Um via Rn, i.e., the S – Rn – Um link, respectively, and
hmFad~CN(0,δFad2) is the channel coefficient representing the effect of multi-path fading and/or multi-reflection on the RTs.
Let GS(θ, φ) and GUm(θ, φ), respectively denote directivity patterns of the transmit antenna of S and the receive antenna of Um where θ and φ are respectively the zenith and azimuth angles. For given locations of S and Um and given antenna’s orientations, we can calculate the values for θ and φ, hence obtaining the values for transmit/receive directivities for wireless links. Let
GSS→X≜GS(θX,φX) be the transmit directivity for the link from S to a given point X, and let
GUmY→Um≜GUm(θY,φY) be the receive directivity for the link from a given point Y to Um. Using these transmit/receive directivities and the free-space path loss (FSPL) model, we can determine
hmLoS and
hSRnUmRef as
where
λ04πdSUm and
λ04πdSRnUm are the loss factors for the FSPL model with the wavelength λ0; dSUm is the distance between S and Um; dSRnUm = dSRn + dRnUm is the distance of the S – Rn – Um link; dSRn and dRnUm are the distances between S and Rn and between Rn and Um, respectively; ψRn = βRnejϕRn is the reflecting coefficient of Rn with βRn ≤ 1 and ϕRn ∈ [0, 2π]; and
ϕSUm-2πdSUmλ0 and
ϕSUnUm=2πdSRnUmλ0 are the phase shifts caused by wave propagation over the distances dSUm and dSRnUm.
As shown in (
1),
hm is a Rice distributed RV. Let
h ~ Rice(Ω,
K) be a general Rice distributed RV, then the cumulative distribution function (CDF) of |
h|
2 is expressed as [
10]:
where
μ=σFad-2 and
Bk=(1-e-K∑i=0k-1Kii!)/k!.
Next, we study the effect of PD caused by non-ideal RTs on the received signal at the users. Regarding the NOMA principle,
S transmits a combined signal
xS=α1x1+α1x2 to the users where
x1, E{|
x1|
2} =
P0, and
x2, E{|
x2|
2} =
P0, are respectively the desired signals for
U1 and
U2;
α1 and
α2 are the PA factors of NOMA satisfying
α1 +
α2 = 1. When
xs is reflected from the RTs, the PD caused by the non-ideal RTs make it distorted. The effect of non-ideal hardware on system performance has been widely studied in [
14–
16] and is characterized as a complex Gaussian noise
κRnPD~CN (0,τRnP0) with the PD factor
τRn ≪ 1. Using (
1), the received signal for
Um in the presence of PD is given by
where
nm ~
CN(0,
N0) is the additive white Gaussian noise (AWGN) at the receive antenna, and
x^s≜xs1-τRn+κRnPD is the distorted signal reflected on
Rn. The factor
1-τRn is the power-constraint factor for guaranteeing

, or equivalently, the IRS does not add any power to the reflected signal. We can rewrite (
5) as
It is seen from (
6) that
ĥm ~ Rice(Ω̂
m,
K̂m) is still a Rice distributed RV, and
n^m~CN (0,N0+σPD2) is the total noise including the AWGN and the noise caused by the PD. The values for Ω̂
m,
K̂m, and
σPD2 are calculated as the follows.
The phase shift of each RT, i.e.,
ϕRn, plays an important role in system performance. It defines whether the received signals at
Um via the dominant links are constructive or destructive. Let us consider the distance-propagation phase shift of the LoS link, i.e,
ϕSUm, as the standard reference in the phase shift at
Um, the signal-combining phase shift denoted by
ϕRnsc, which measures the difference between the distance-propagation phase shift on the
S-
Rn-
Um link and
ϕSUm.
ϕRnsc is calculated as follows [
17].
Using
ϕRnsc,
ψRn,
hmFad, and the formulas for channel coefficients
hmLoS and
hSRnUmRef (given in (
2) and (
3)), we can calculate Ω̂
m and
K̂m using a similar approach in [
10]:
Then, using the fact that the sum of independent complex Gaussian RVs is a complex Gaussian RV with its variance being the sum of all variances, we can calculate
σPD2 as
III. SINR Distribution Characterization and Average Achievable Rate Analysis
For convenience in analyzing the SINRs, we rewrite (
5) as
According to the SIC principle of NOMA, the SINRs for the signal x2 at both users, i.e., Um, m = {1, 2}, are given by
where
γm=P0/(N0+σPD,m2), and the SINR for the signal x1 at U1 is given by
Using Shannon’s law, we can calculate the achievable rates (also known as the ergodic capacities) in bits/s/Hz for the signal x2 at both users as
and for the signal x1 at U1 as
where
Y = min(
Y1,
Y2) is the condition for guaranteeing successfully decoding
x2 at both users (note that
U1 must decode
x2 before decoding its information
x1), and
g ~ CN (0,
λImSIC) in (
13) represents the residual signal of
x2 caused by the imperfect SIC receiver at
U1 with variance
λSICIm =
ζE{|
hSU1|
2} and the SIC imperfection factor ζ ≤ 1.
Proposition 1
The CDF of X denoted by FX(t) = Pr(X < t) is approximated as
where ρm = μ/(α1γm), and η = λImSICα1/(μα2).
Proof
The approximate CDF of
X is calculated as
FX(
t) ≈ Pr(|
ĥ1|
2 < (1 +
γ1 |
g|
2 α2)
t/(
γ1α1)). Using the probability density function (PDF) of the exponential distribution given by
f|g|2 (
t) =
λImSIC exp (−
λImSICt)and (
4), we obtain
FX(
t) via solving the following equation.
Using [
18, Eq. (3.381.3)] and some manipulations, we obtain (
16). The proof for Proposition 1 is completed.
Proposition 2
The CDF of Y denoted by FY(t) = Pr(Y < t) is equal to one if t > α2/α1, and otherwise, it is calculated as
Proof
Since
Y = min(
Y1,
Y2), we can rewrite
FY(
t) as
FY(
t) = 1 − Pr (
Y1 >
t)Pr(
Y2 >
t). Then, substituting (
4) into it yields (
18). The proof for Proposition 2 is completed.
Using Propositions 1 and 2, we can obtain the theoretical results for AARs as follows.
Proposition 3
The theoretical AAR expressions for the signals
x1 and
x2 are respectively given in the
equations (19) and
(20) shown in the top of the next page, where
Ck=∑q=0kB1,qB2,k-q(γ1)-q(γ2)-k+q.
Proof
According to [
19], the AAR for the signal
xm,
m = {1, 2}, is calculated as
Substituting (
16) and (
17) into (
21) and using some manipulations, we can obtain (
19) and (
20). The proof for Proposition 3 is completed.
IV. Numerical Results and Discussion
In this section, we present the numerical results for the AAR and discuss the effect of different key parameters on it. The theoretical results are derived for a general system, such as any type of transmit/receive directivity of the device antennas, frequency, wireless indoor environment, and device locations. For the simulation, we chose a specific setup for our system. Without loss of generality, we set the phase shifts of the IRS as
ϕRn = 2
π × mod(
dSRn +
dRnUm –
dSUm,
λ0)/
λ0 to gain the strongest received signal strengths (RSSs) at the users,
βRn = 0.9 and
τRn = 0.1 where
n = 1,..., 2
Ncol. The coordinate setups are shown in
Fig. 2, and the setup of other parameters is listed in
Table 1 [
20]. The transmit antenna is a half-wavelength dipole with its orientation illustrated in
Fig. 2, and its directivity pattern is given in
Table 1. The receive antennas have the same directivity for all directions. The numerical results include the theoretical AARs obtained using (
19) and (
20), and the simulation results are obtained by evaluating a simulation system using MATLAB. The good match between the theoretical and the simulation results confirms the accuracy of our study.
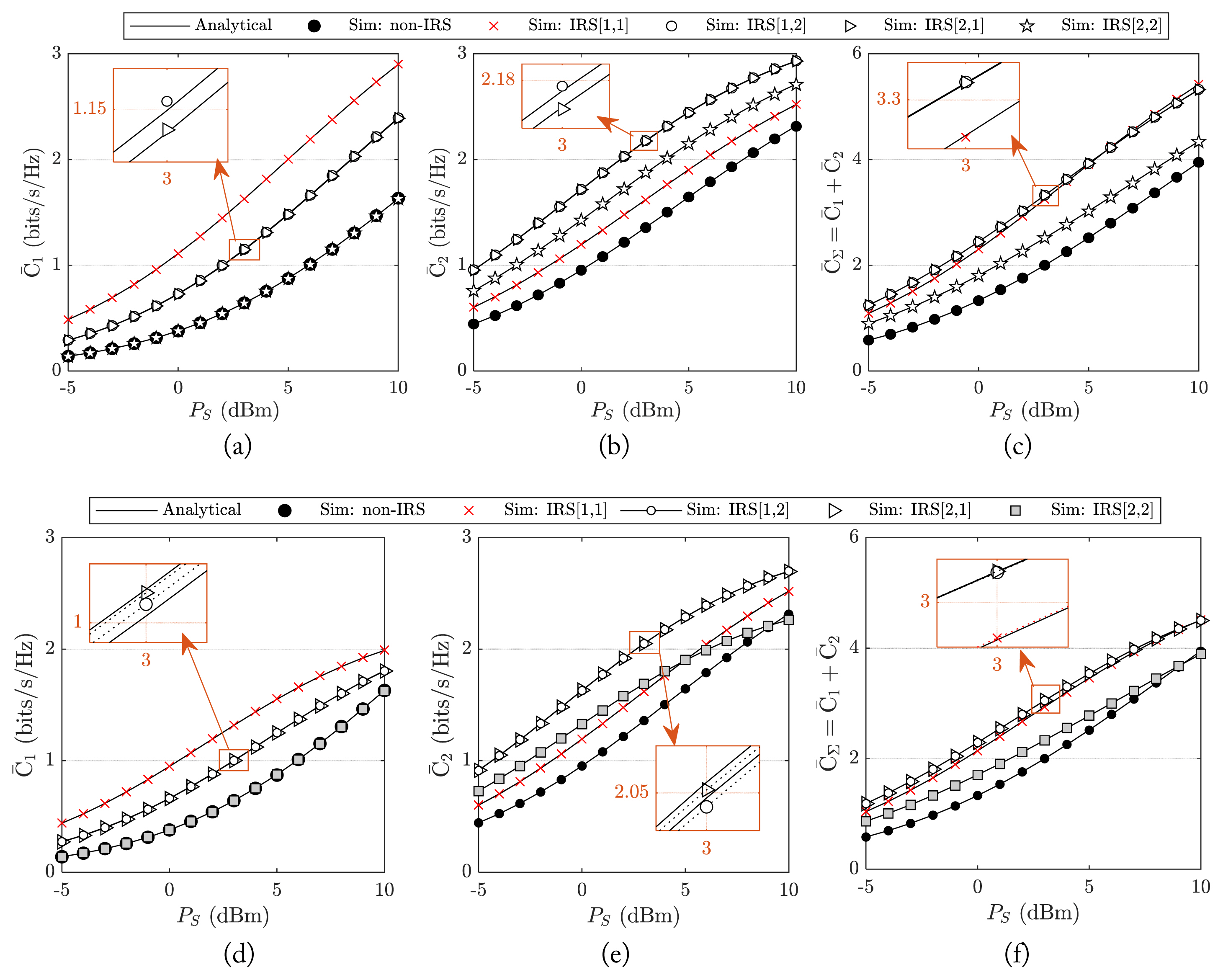
In
Fig. 3, we show the advantage of using the IRS to assist NOMA communication via examining a simple IRS, including 2 RTs. We consider four possible cases denoted by IRS[
m1,
m2],
m1,
m2 ∈{1, 2}, which indicates that the first and the second RTs are allocated to
Um1 and
Um2, respectively. The AARs for
x1,
x2 and total AAR,
C̄∑ =
C̄1 +
C̄2, for the ideal-IRS scenario (without the presence of the PD) are shown in
Fig. 3(a)–3(c), respectively, and those of the non-ideal-IRS scenario (with the presence of the PD) are shown in
Fig. 3(d)–3(f), respectively. The AARs are displayed as increasing functions of
PS. Without the IRS, the received signal at each user propagates on the direct link and multi-path fading channel. Therefore, the AARs are very low, as shown as the lowest curves in
Fig. 3. When the IRS is utilized, the AARs are significantly enhanced even with the presence of the PD. Although different levels of AAR enhancement are observed, these results still indicate the important role of the IRS in improving the RSSs at the users. As shown in
Fig. 3(c) and 3(f), the total AARs for the cases of IRS[
1,
2] and IRS[
2,
1] (in these cases, the IRS assists the communication for both users) achieve better values than other cases.
In
Fig. 4, we adopt the best IRS setup for the case of
PS = 0 dBm with
τPD = 0.1 (found in
Fig. 3, i.e., IRS[
2,
1]) and then investigate the effect of the PA factors on the total AAR. The advantages of the NOMA scheme are confirmed by investigating a reference orthogonal multiple access (OMA) scheme. Due to the advantageous location of the near user, the system achieves a highest or lowest total-AAR when allocating all resources to the near user or the far user, respectively. When the SIC imperfection factor
ζ increases, the total AAR becomes worse. For a performance comparison, we use a conventional OMA scheme, which defines the AAR for
Um,
m = {1, 2}, as
and the total AAR for OMA is given by
where
υm ∈ (0, 1),
υ1 +
υ2 = 1, is the resource allocation (RA) factors for OMA (e.g., time allocation factor for TDMA or bandwidth allocation factor for FDMA). Compared to OMA, NOMA can achieve a higher total AAR in the presence of PD and imperfect-SIC. When
ζ is sufficiently large, NOMA yields a lower performance compared to OMA. In
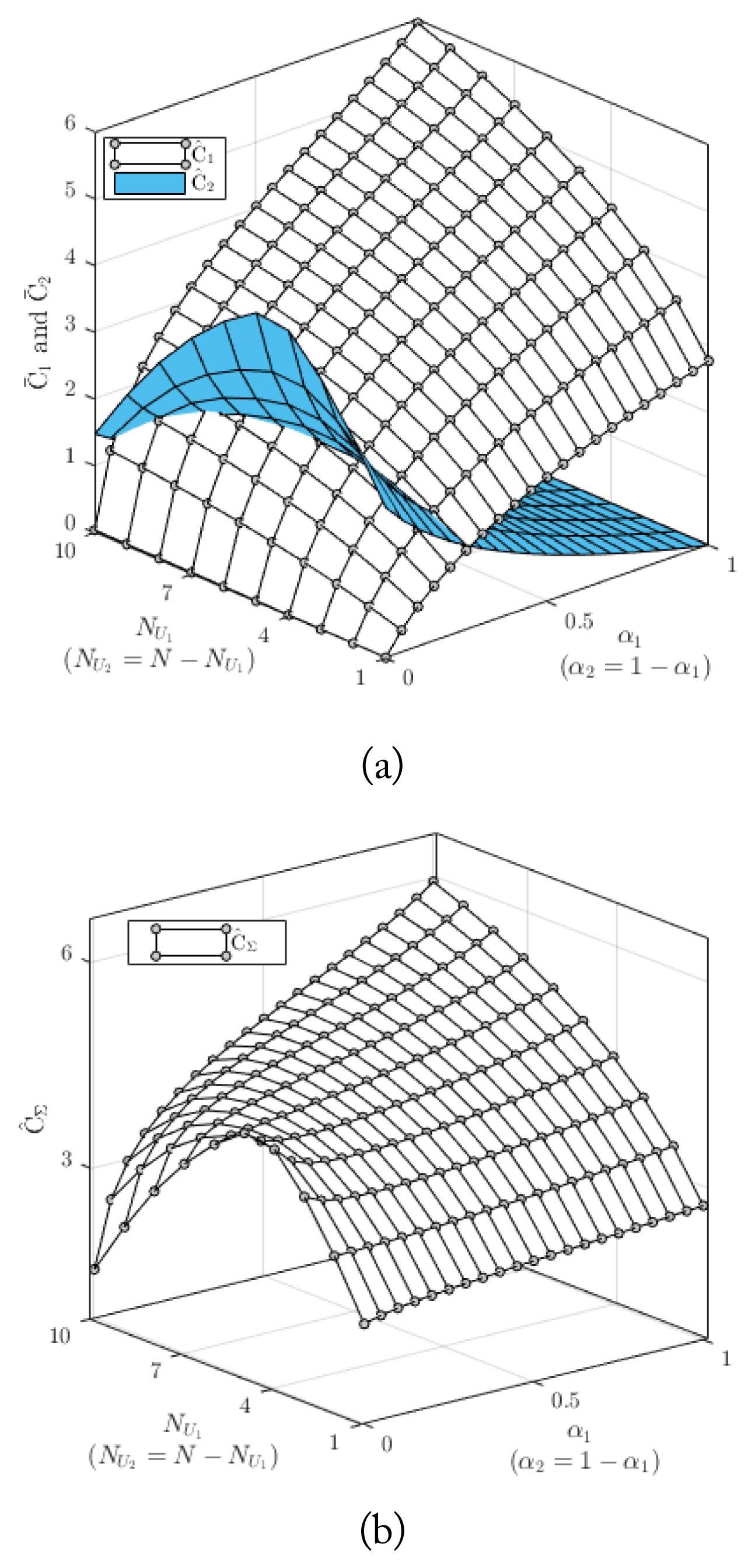
Fig. 5, we show the joint effect of the RT-allocation strategy and PA factors, i.e.,
α1 and
α2, on the AAR. Because the size of each RT is relatively small compared to the wave-propagation distances, the difference in distance between reflecting links is trivial. It is reasonable to assume that the signal attenuations of reflecting links toward a user are similar. For this reason, the RT allocation strategy is as follows. Let
NU1 be the number of RTs allocated to
U1. These
NU1 RTs are assigned from left to right and from top to bottom. The other
NU2 =
N –
NU1 RTs are assigned to
U2. For a given value of
NU1,
C̄1 increases, while
C̄2 decreases when we increase
α1 and vice versa. This is because the power resource allocated for the users is defined by
α1. For given PA factors,
C̄1 is shown as an increasing function of
NU1, whereas
C̄2 improves with the first increase in
NU1 and then reaches the optimal value. Finally, it degrades with further increases in
NU1. The trend of
C̄2 is explained as follows. Since both users need to decode
x2 successfully, the IRS needs assist both users to gain the highest value of
C̄2. Therefore, using very high or very low values of
NU1 does not yield good values for
C̄2. Although the highest total AAR is observed at (
NU1 = 10,
α1 = 1), the NOMA system does not use this configuration. The reason is that at this point, all system resources, including
PS and RTs, are allocated to
U1; hence,
U2 is disconnected from the network. For our proposed NOMA system, we focus on the points lying on the intersection curve of the two user-AAR surfaces denoted by
ℓ(NU1,α1*), on which two users can communicate with the source at the same AAR. Let the highest value observed on
ℓ(NU1,α1*) be the optimal NOMA-AAR
ℓ*=maxℓ(NU1,α1*) and its respective coordinate
(NU1,α1*) be the optimal solution for ℓ
*. The trends of ℓ
* and
(NU1,α1*) are studied in
Fig. 6.
In
Fig. 6, we consider an IRS with a size of 2-by-
Ncol RTs and then plot the optimal NOMA-AAR as shown in
Fig. 6(a) and its respective optimal solution, i.e., optimal PA factors as shown in
Fig. 6(b) and optimal RT-allocation as shown in
Fig. 6(c) and 6(d), under different parameters of
PS and
ζ.
Fig. 6(a) shows that the more RTs are used, the higher value for optimal NOMA-AAR is achieved. When the IRS’s size is sufficiently large, the increase in size does not gain much improvement in optimal NOMA-AAR. Therefore, the size of the IRS should be chosen carefully to achieve a reasonable trade-off between performance and cost. For instance, at
ζ = 0.04 and
PS = 0 dBm, the 2-by-1 and 2-by-4 IRSs can support 1 bit/s/Hz and 2 bit/s/Hz optimal NOMA-AAR, respectively. In
Fig. 6(b)–6(d), we show the trends of the obtained optimal solutions. Regarding the NOMA principle, first, both users need to decode the signal allocated with stronger power, which is
x2 for our proposed system, and consider the rest signals as interference, as shown in (
12). After successfully decoding
x2,
U1 eliminates the signal
x2 from its received signal and then decodes its desired signal
x1, which is allocated with lower power. The allocated power for each signal is defined by the PA factors. Compared to
x2, the decoding process of
x1 deals with lower interference, which is caused by the imperfect-SIC decoder as shown in (
13). For this reason, the AAR for
x2,
C̄2, significantly depends on the PA factors, and
C̄2 increases when
α1* decreases (or equivalently
α2* increases). Moreover,
C̄1 significantly depends on the RSS at
U1. Hence,
C̄1 is enhanced when more RTs are allocated to
U1. Using the above assessments, it is easy to explain the trends of
α1* and
NU1*. When the total number of RTs increases, the signal quality at users becomes greater, and the system can boost both AARs at two users by allocating more RTs to
U1 and using higher values for
α2* (or equivalently using lower values for
α1*). Therefore,
α1* is a decreasing function of
Ncol, as shown in
Fig. 6(b), whereas
NU1* and
NU2* are increasing functions of
Ncol, as shown in
Fig. 6(c) and 6(d). Moreover,
NU1* increases more significantly than
NU2*. On the other hand, the increase in transmit power
PS or the decrease in the SIC-imperfection factor
ζ also give the same effect on the signal quality at the users.
Hence, the smaller value for
α1* and higher values for
NU1* are observed when PS increases or ζ decreases.
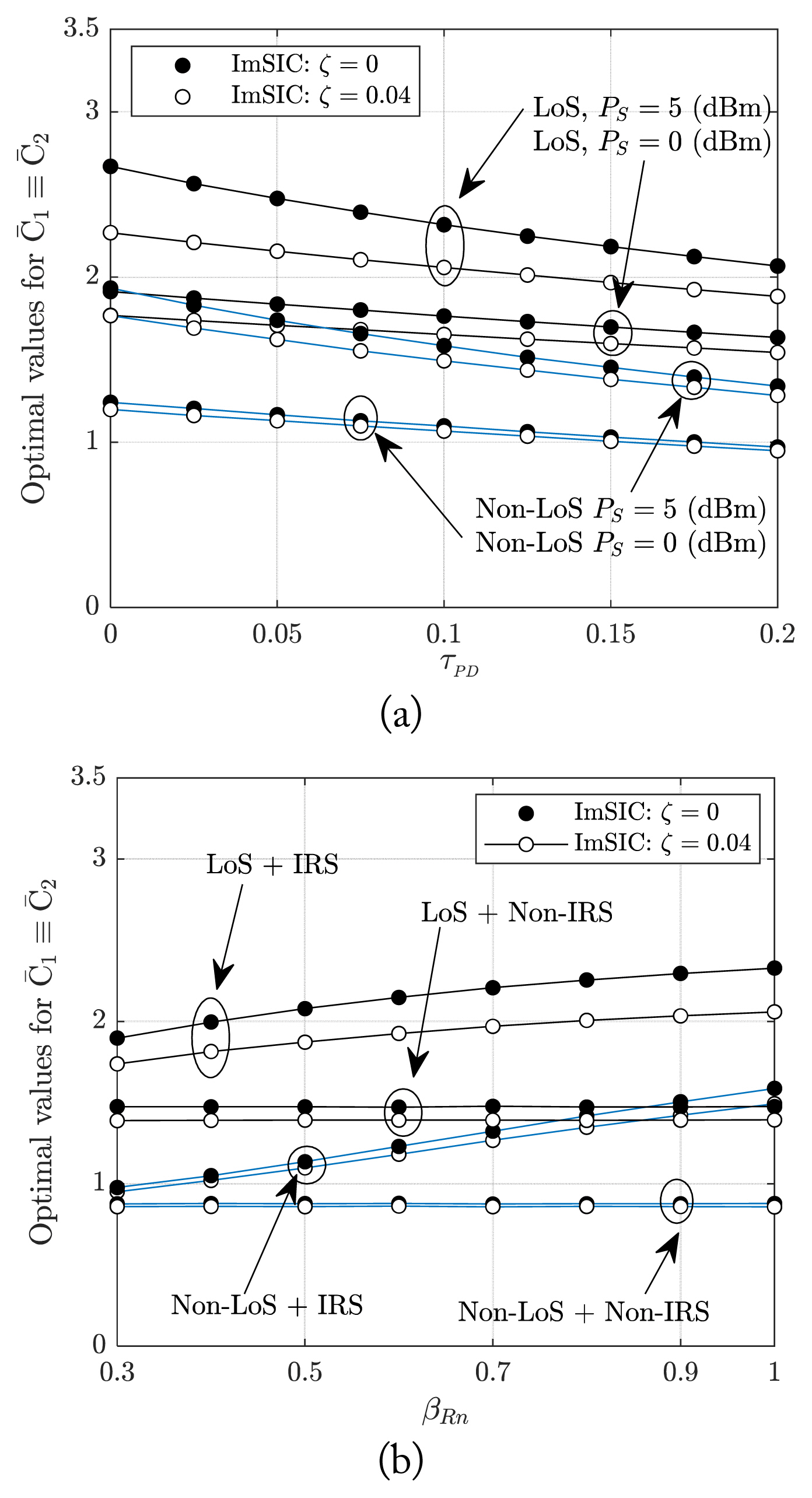
In
Fig. 7, we show the effects of the PD factor
τPD and the reflection amplitude
βRn on the system performance for two cases: with and without the presence of the LoS links. The results for the non-LoS case are obtained by set the source-to-user distances in (
8) by very large values, i.e.,
dSUm → ∞. The optimal NOMA-AAR drops around 0.8 bits/s/Hz when the LoS links are not available. This indicates the importance of the LoS links; however, without the LoS links, the system can achieve a moderately optimal NOMA-AAR with the help of the reflecting link and the multi-path fading channel. When
τPD increases, the total noise at each user increases. Hence, the optimal NOMA-AAR is displayed as a decreasing function of
τPD as shown in
Fig. 7(a). With the presence of a multi-path fading channel and/or LoS links, the influence of the PD on the optimal NOMA-AAR can be reduced; however, when the user is blocked and its communication only relies on the reflecting links, the value of
τPD becomes a crucial factor to performance.
Fig. 7(b) presents the optimal NOMA-AAR for different values of
βRn. When
βRn increases, the stronger received signal strengths are achieved at the users. Therefore, the optimal NOMA- AAR is shown as an increasing function of
βRn. Moreover, the optimal NOMA-AAR for the case using the IRS is higher than that for the non-IRS case. This indicates the effectiveness of the IRS in improving system performance. Since
βRn only affects the quality of the reflecting links, the influence of low
βRn values can be reduced in the case of the presence of the LoS links or the stronger multi-path fading channel.
 , or equivalently, the IRS does not add any power to the reflected signal. We can rewrite (5) as
, or equivalently, the IRS does not add any power to the reflected signal. We can rewrite (5) as , or equivalently, the IRS does not add any power to the reflected signal. We can rewrite (5) as
, or equivalently, the IRS does not add any power to the reflected signal. We can rewrite (5) as