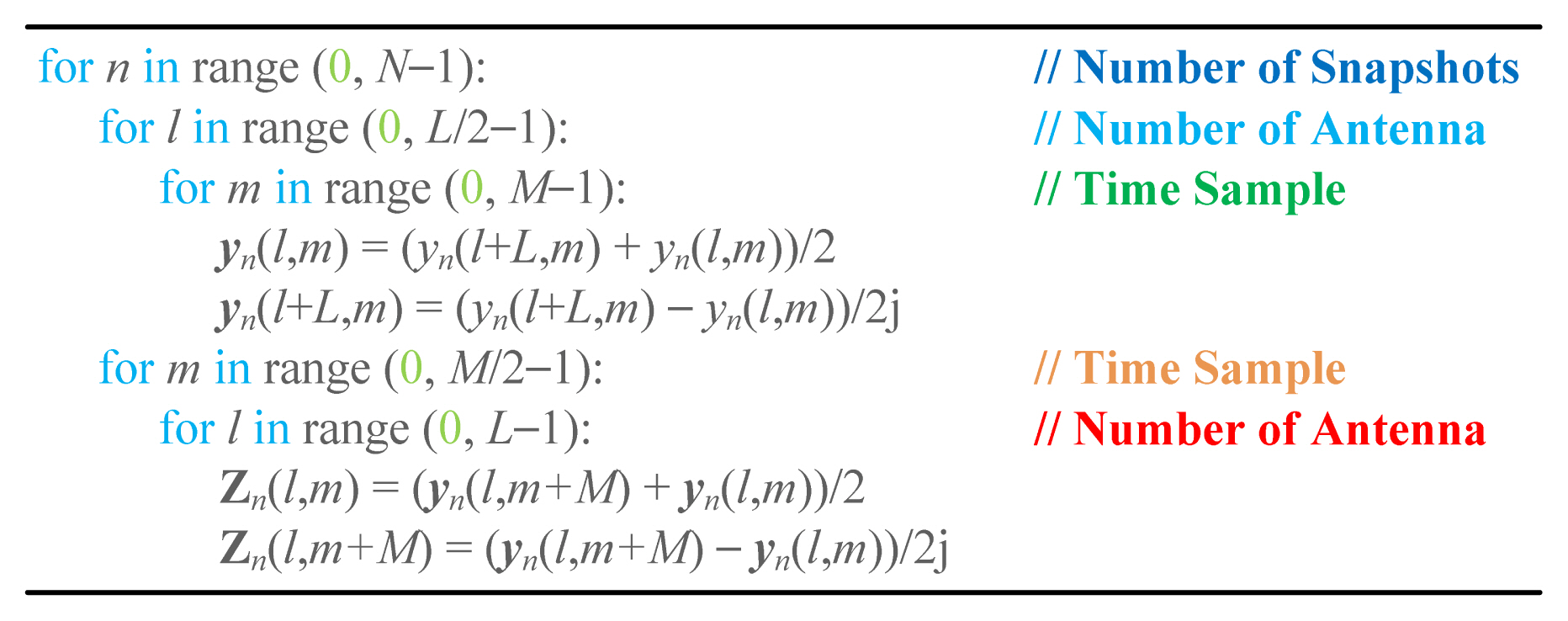Low-Complexity 2D-MUSIC for Joint Range and Angle Estimation of Frequency Modulated Continuous-Wave Radar
Article information
Abstract
A pre-processing technique is proposed to reduce the complexity of two-dimensional multiple signal classification (2D-MUSIC) for the joint range and angle estimation of frequency-modulated continuous-wave (FMCW) radar systems. By using the central symmetry of the angle steering vector from a uniform linear array (ULA) antenna and the linearity of the beat signal in the FMCW radar, this pre-processing technique transforms 2D-MUSIC from complex values into real values. To compare the computational complexity of the proposed algorithm with the conventional 2D-MUSIC, we measured the CPU processing time for various numbers of snapshots, and the evaluation results indicated that the 2D-MUSIC with the proposed pre-processing technique is approximately three times faster than the conventional 2D-MUSIC.
I. Introduction
In frequency-modulated continuous-wave (FMCW) radar systems, multiple signal classification (MUSIC) has been extensively used for estimating the angle of multiple targets with high resolution [1–3]. Recently, as a method for more accurate target detection, two-dimensional (2D)-MUSIC for joint range and angle estimation has been studied for FMCW radar systems [4–6]. However, the complexity of 2D-MUSIC increases exponentially compared to that of one-dimensional (1D)-MUSIC for angle estimation [7, 8]. To reduce the complexity of 2D-MUSIC, 2D-gold-MUSIC was proposed in [9, 10]. On the basis of 1D-gold-MUSIC, 2D-gold-MUSIC can reduce complexity by searching only a portion of the 2D-MUSIC spectrum [9]. Nevertheless, the complexity of 2D-gold-MUSIC still remains because all operations are performed with complex values.
To transform 1D-MUSIC from complex values into real values, various methods have been proposed. The unitary MUSIC algorithm for a centrosymmetric antenna array was proposed in [11], which can convert the complex covariance matrix and complex steering vector into a real matrix and real vector through unitary transformation. In [12, 13], a more effective pre-processing technique was proposed with less computational overhead than unitary MUSIC by using the angle phases of the incident signal as the central symmetry. This pre-processing converts the complex angle steering vector into real vectors. However, the range steering vector is still complex when this technique is applied to 2D-MUSIC.
In this paper, we propose a novel pre-processing technique that can transform complex range and angle steering vectors into real vectors for 2D-MUSIC. The simulation results indicate that the performance is the same as that of the conventional 2D-MUSIC, and the computational complexity can be significantly reduced. The remainder of this paper is organized as follows. In the estimation model, the 2D-MUSIC algorithm is briefly described. We then propose the pre-processing algorithm for 2D-MUSIC and show the simulation results to compare them with conventional 2D-MUSIC. Finally, the conclusion is presented.
II. Estimation Model
In the time domain, the FMCW radar’s beat signal at the l-th antenna (l ∈ {1,2,..,L}, where L denotes the number of antennas) is expressed as
where ak, τk, and θk denote the complex amplitude, time delay, and angle of the k-th target (k ∈ {1,2,..,K}, where K is the number of targets), respectively. fc denotes the carrier frequency. B and T denote the sweep bandwidth and time for one chirp, respectively.
where
The first step of 2D-MUSIC for joint range and angle estimation is to vectorize the received signal such that
where d̄l,n = [yn(l, 1), K, yn(l, M)]T. The covariance matrix for xn is defined as follows:
where (·)H denotes the Hermitian transpose. The corresponding eigenvalue decomposition is as follows:
where λi (λ1 > λ2 > ⋯ > λLM) denotes the i-th eigenvalue and ei the corresponding eigenvector of the matrix R, respectively. Es and En represent the signal subspace and noise subspace of matrix R, respectively. Using the noise subspace En, we can establish the 2D-MUSIC spectrum for joint range and angle estimation, such as
where v(R, θ) = [a1(θ), …, aL(θ)] ⊗ [b1(R), …, bM(R)], and ⊗ denotes the Kronecker product. P(R,θ) has peaks at the localization of targets through a 2D search.
III. Proposed Pre-processing Technique
To reduce the computational complexity of 2D-MUSIC for joint range and angle, we propose a pre-processing technique that can make a 2D-MUSIC algorithm based on real values. The number of ULA antennas and the number of time-axis samples are assumed to be even. Before the vectorization of Eq. (3), two vectors are formed as follows:
After performing the operations of y1,n(m) and y2,n(m) using q1,n and q2,n, an (L × 1)-dimensional vector yn can be expressed as follows:
where
and b=[bm,n(R1),⋯,bm,n(RK)]T. w represents an (L×1)-dimensional AWGN vector because the addition and subtraction between AWGN is still AWGN. The (l, k)-th element in matrix A, A(l, k), is determined as follows:
The next step is to form the (L×M/2)-dimensional matrices Y1,n and Y2,n as follows:
Assuming Z1,n = (Y2,n+Y1,n)/2 and Z2,n = (Y2,n−Y1,n)/2j, the (L × M)-dimensional matrix Zn is determined as follows:
where
Wn is also an AWGN matrix. The (k,m)-th element of the matrix B, B(k, m) is determined as follows:
Consequently, yn(l,m) in (2) can be transformed into a signal with a real-valued steering vector by using the proposed pre-processing technique and can be expressed as follows:
where
where
Therefore, using the proposed pre-processing technique and taking only the real part, 2D-MUSIC can be transformed from a complex value to a real value. Through a similar process, the proposed pre-processing technique can be applied to 2D-gold-MUSIC or 3D-MUSIC for the estimation of range, azimuth angle, and elevation angle. Fig. 1 also shows the pseudo code of proposed pre-processing.
We proposed a pre-processing algorithm to reduce the complexity of the computation of the 2D-MUSIC algorithm. Also, the proposed pre-processing algorithm can be applied to any 2D-MUSIC algorithm. Therefore Table 1 presents the comparison results for the computational complexity of the conventional 2D-MUSIC and the proposed 2D-MUSIC. It is assumed that eigenvalue decomposition is performed by the Jacobi method [14], where Q is the number of iterations. In the spectrum search process, as and rs are the angle and range resolutions, respectively. Rmax denotes the maximum range. As shown in Table 1, the proposed 2D-MUSIC reduces the multiplications by about four times and the additions by about three times in the calculation of the covariance matrix. In addition, both multiplications and additions are reduced by about four times in the eigenvalue decomposition. Moreover, the division and arctangent operations are reduced by two times. In the process of the MUSIC spectrum search, multiplications and additions are reduced by about four times and two times, respectively.
IV. Simulation Results
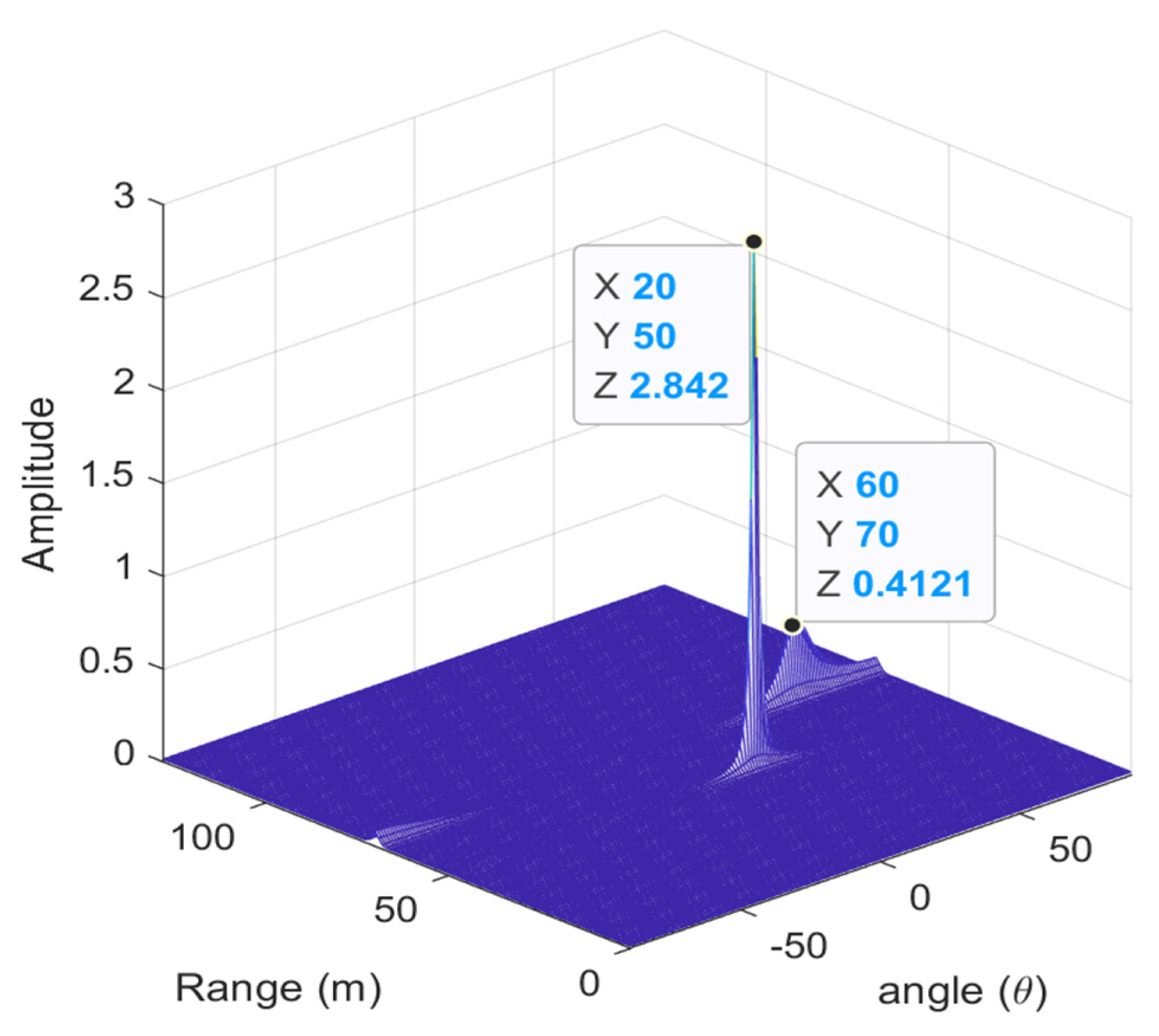
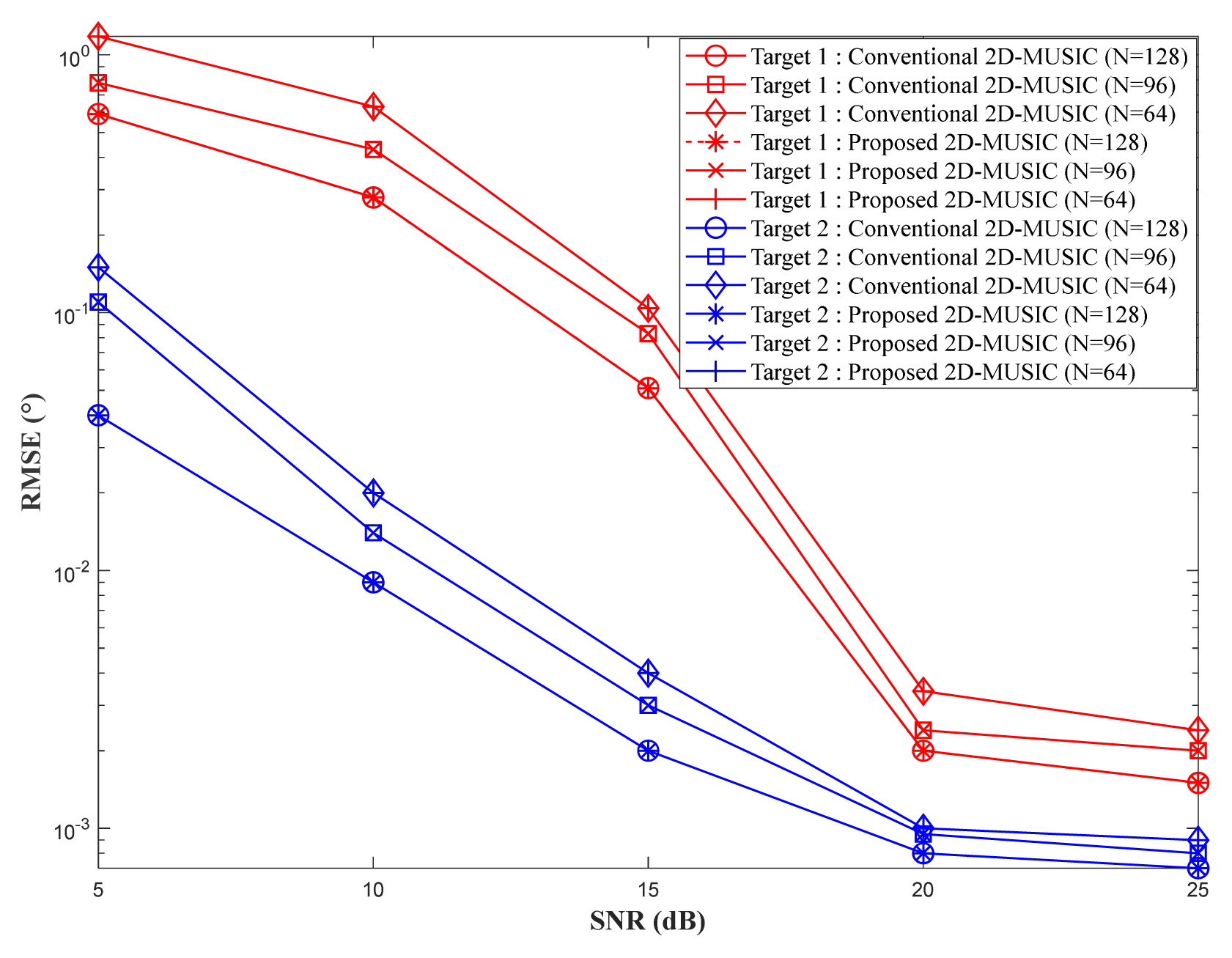
To evaluate the performance of the proposed pre-processing technique for 2D-MUSIC, we assume that there are two uncorrelated stationary targets located at (R1, θ1) = (50 m, 20°) and (R2, θ2) = (70 m, 60°). There are four or eight receiving antennas, and the number of snapshots is 64, 96, and 128. The range and angle resolution are 0.1 m and 0.1°, respectively. Figs. 2–5 illustrate the variations of the azimuth angle and range estimation root mean square error (RMSE) with signal-to-noise ratio (SNR), respectively, where 1,000 Monte Carlo simulations were performed. In addition, Fig. 6 shows a spatial spectrum when SNR is set to 15 dB.
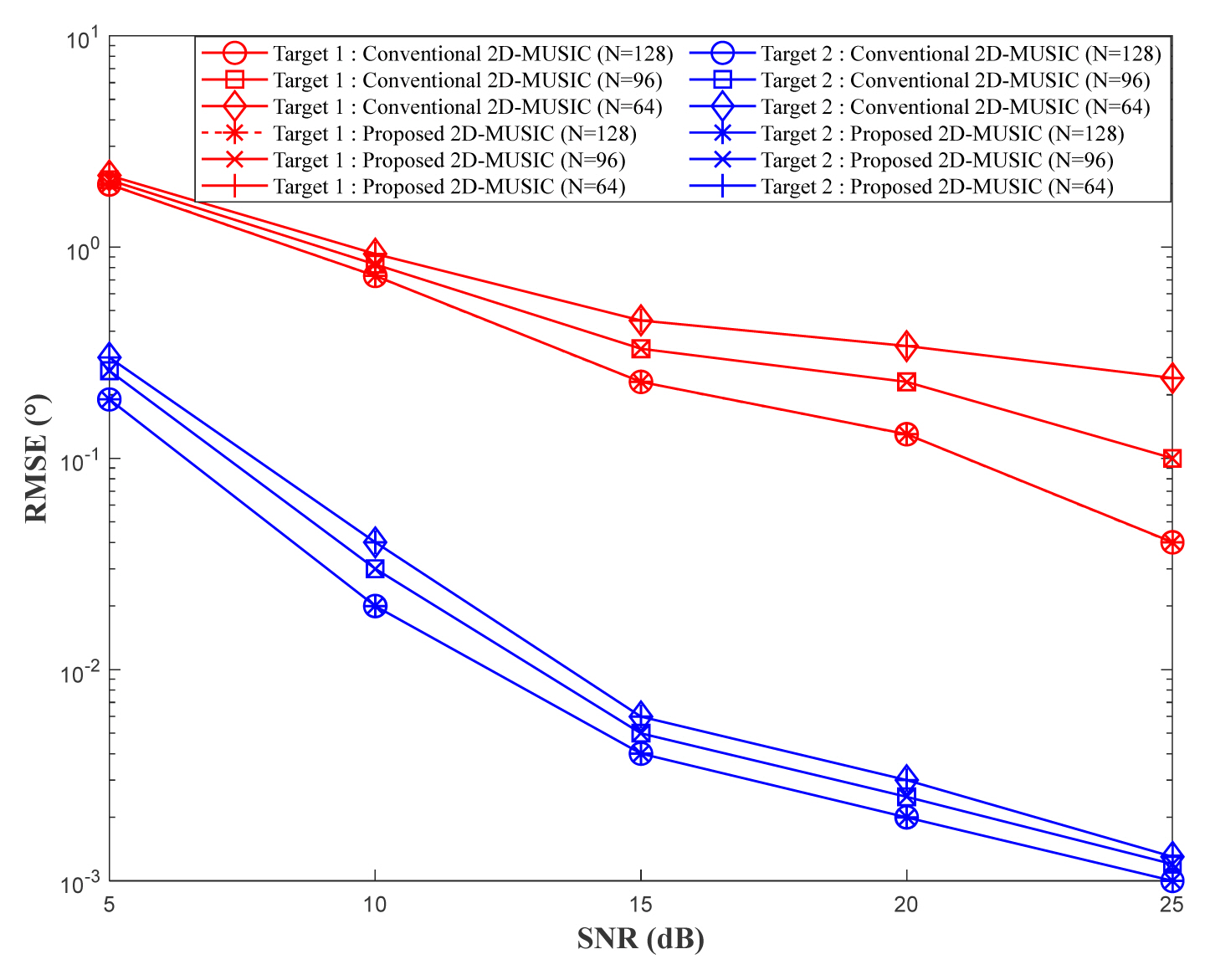
RMSE of azimuth angle estimation from 1,000 Monte Carlo simulations for two targets (M = 64, L = 4, K = 2, Q = 1,000).
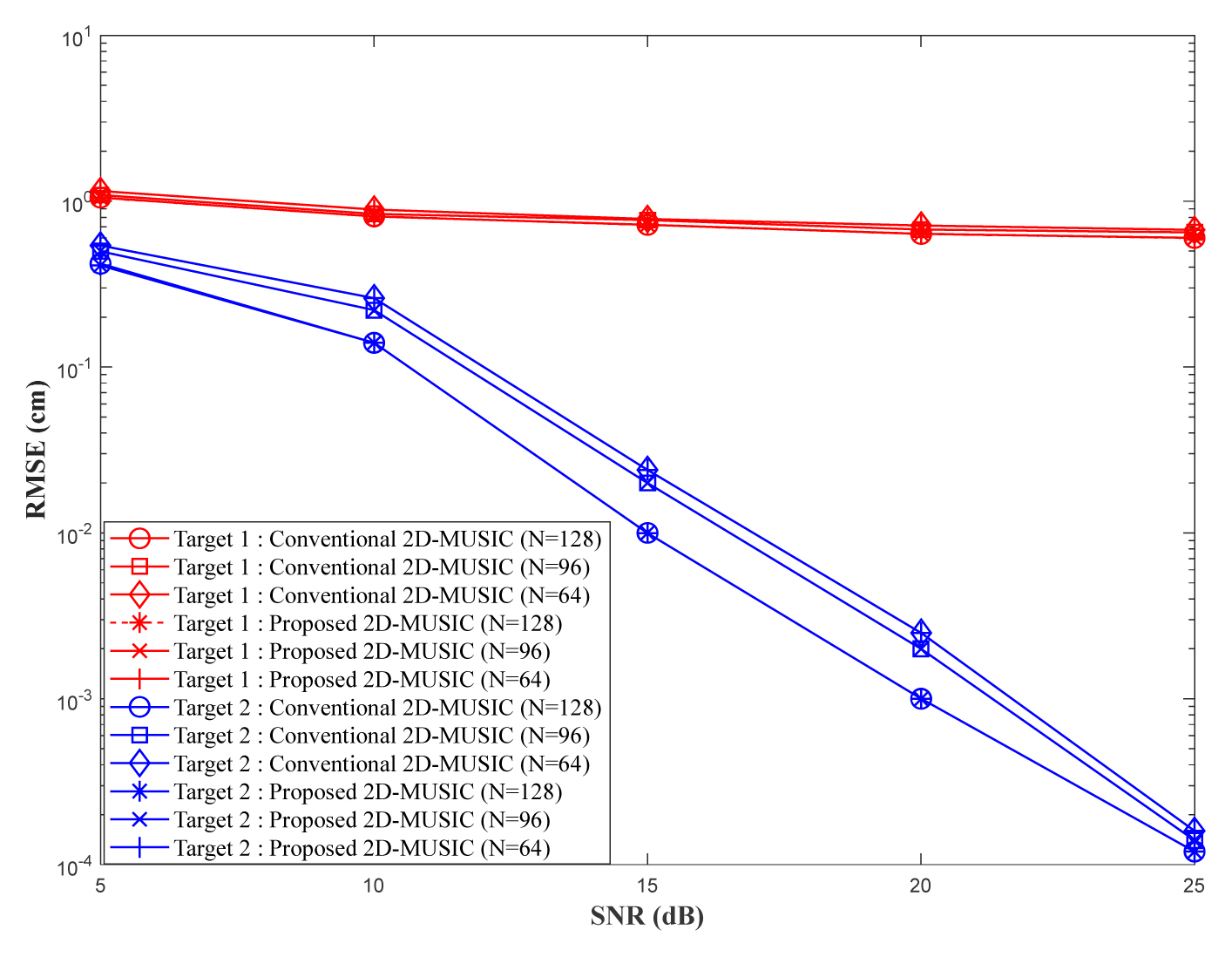
RMSE of range estimation from 1,000 Monte Carlo simulations for two targets (M = 64, L = 4, K = 2, Q = 1,000).
RMSE of azimuth angle estimation from 1,000 Monte Carlo simulations for two targets (M = 64, L = 8, K = 2, Q = 1,000).

RMSE of range estimation from 1,000 Monte Carlo simulations for two targets (M = 64, L = 8, K = 2, Q = 1,000).
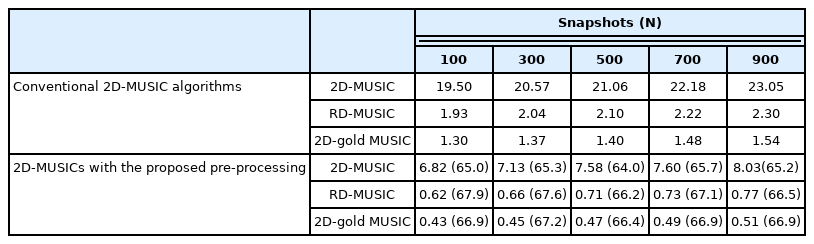
As mentioned in Section III, the proposed pre-processing techniques can be applied to various 2D-MUSIC algorithms and can reduce the computational complexity. Table 2 shows the evaluation results for the runtime, which corresponds to the computational complexity between the existing 2D-MUSIC algorithms and 2D-MUSICs with the proposed pre-processing technique. Basic 2D-MUSIC, 2D-gold-MUSIC [15], and reduced-dimension (RD)-MUSIC [16] algorithms are considered for evaluation. The timeit in MATLAB instructions can be used to calculate the runtime as in [17], and the runtime is analyzed against the number of snapshots. We can observe from Table 2 that the runtime of the basic 2D-MUSIC using the proposed pre-processing technique is reduced by a maximum of 65.7% compared to the case without pre-processing. In addition, the runtimes of the 2D-gold-MUSIC and RD-MUSIC with the proposed pre-processing technique are reduced by a maximum 67.2% and 67.9%, respectively.
V. Conclusion
In this paper, we propose a novel pre-processing technique to reduce the complexity of the 2D-MUSIC algorithm for the joint range and angle estimation of FMCW radar systems. Using the proposed pre-processing technique, we can transform all complex vectors into real vectors. The simulation results indicate that the runtime of 2D-MUSIC using the proposed pre-processing technique is reduced by approximately three times compared with that of conventional 2D-MUSIC. Because the proposed pre-processing can reduce the computational complexity significantly, it is expected that 2D-MUSIC can be implemented in real-time.
Acknowledgments
This work was supported by the Technology Innovation Program (No. 10080619), funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea), and CAD tools were supported by IDEC.
References
Biography

Yongchul Jung received B.S., M.S. and Ph.D. degrees from the School of Electronics and Information Engineering, Korea Aerospace University, Goyang, South Korea, in 2015, 2017, and 2021, respectively. He is currently a senior researcher with Korea Electronics Technology Institute (KETI), Seongnam, Korea. His research interests include the signal processing algorithm and system-on-chip (SoC) implementation for the radar signal processing system.

Seunghyeok Lee received B.S. and M.S. degrees from the School of Electronics and Information Engineering, Korea Aerospace University, Goyang, South Korea, in 2018 and 2020, respectively. He is currently an engineer with Samsung Company Ltd., Hwasung, Korea. His research interests include the signal processing algorithm and system-on-chip (SoC) implementation for the wireless communication system.

Seongjoo Lee received his B.S., M.S., and Ph.D. degrees in Department of Electrical and Electronic Engineering from Yonsei University, Seoul, Korea, in 1993, 1998, and 2002, respectively. From 2002 to 2003, he was a senior research Engineer with the IT SOC Research Center and the ASIC Research Center, Yonsei University. From 2003 to 2005, he was a senior engineer with the Core Tech Sector, Visual Display Division, Samsung Electronics Company Ltd., Suwon, South Korea. He was a research professor with the IT Center and the IT SoC Research Center, Yonsei University, from 2005 to 2006. He is currently a professor with the Department of Information and Communication Engineering, Sejong University, Seoul. His current research interests include system-on-chip (SoC) design for wireless communication systems, RADAR and Li-DAR signal processing, and SoC design for image signal processing.

Yunho Jung received B.S., M.S., and Ph.D. degrees in electrical and electronic engineering from Yonsei University, Seoul, South Korea, in 1998, 2000, and 2005, respectively. From 2005 to 2007, he was a Senior Engineer with the Communication Research Center, Wireless Device Solution Team, Telecommunication Network Division, Samsung Electronics Company Ltd., Suwon, South Korea. From 2007 to 2008, he was a research professor with the Institute of TMS Information Technology, Yonsei University. He is currently a professor with the School of Electronics and Information Engineering, Korea Aerospace University, Goyang, South Korea. His current research interests include the signal processing algorithm and system-on-chip (SoC) implementation for radar, wireless communication, and image processing systems.