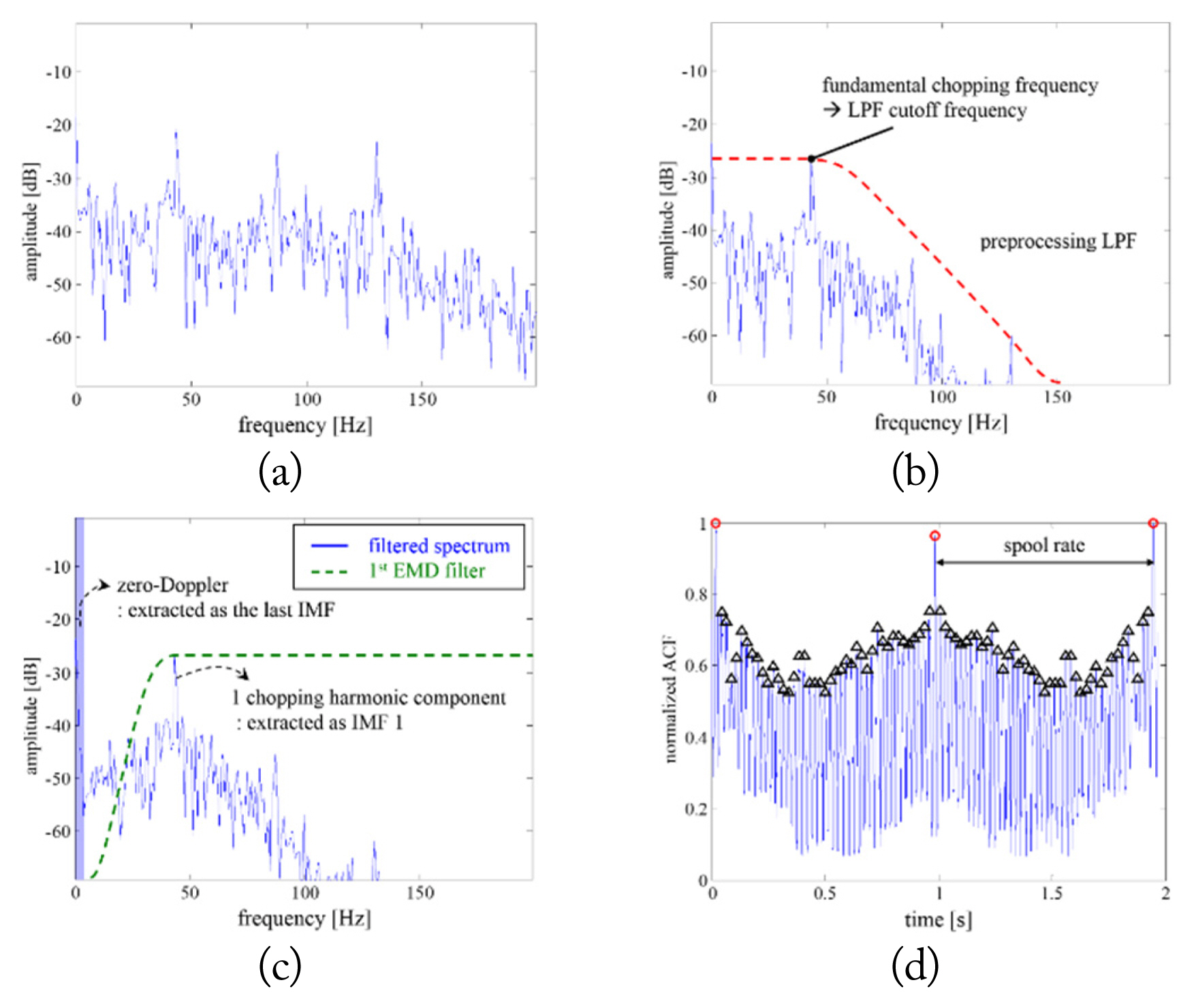
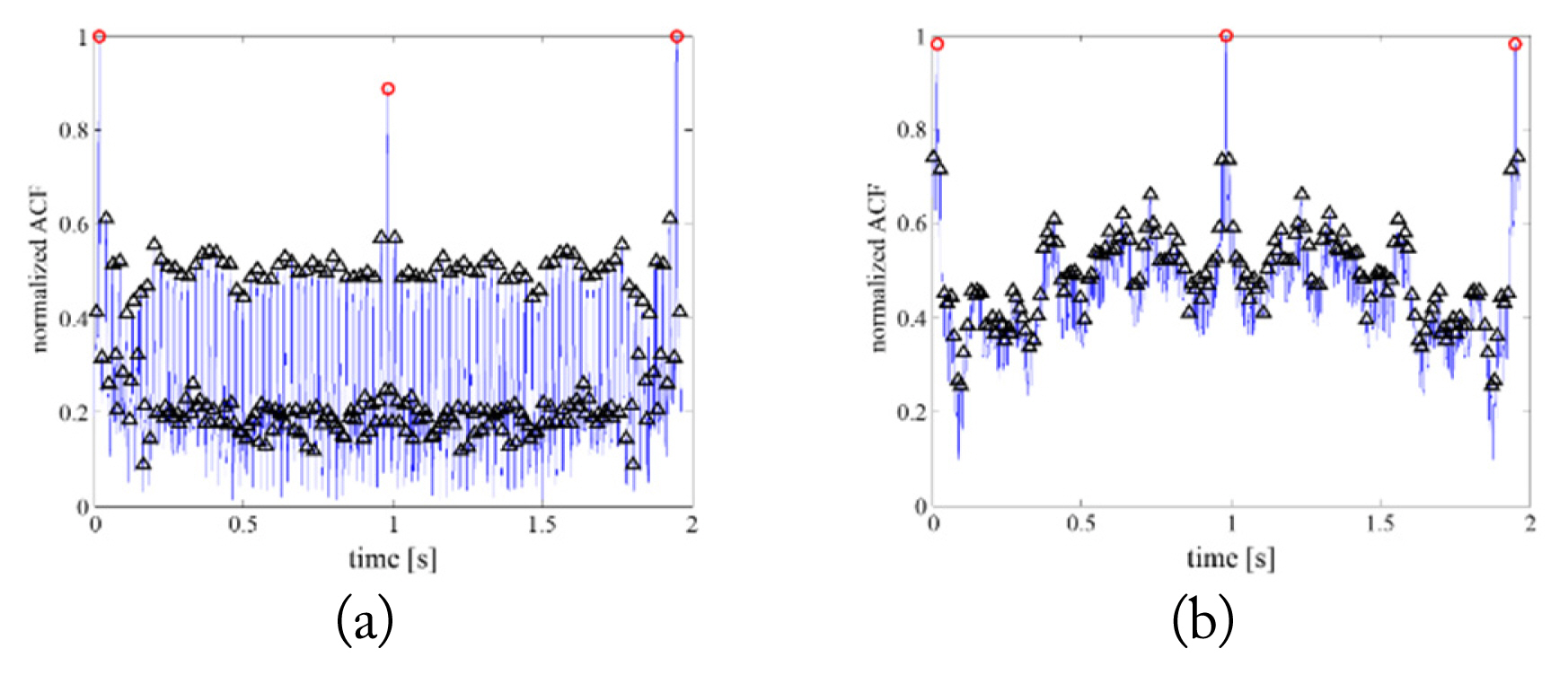
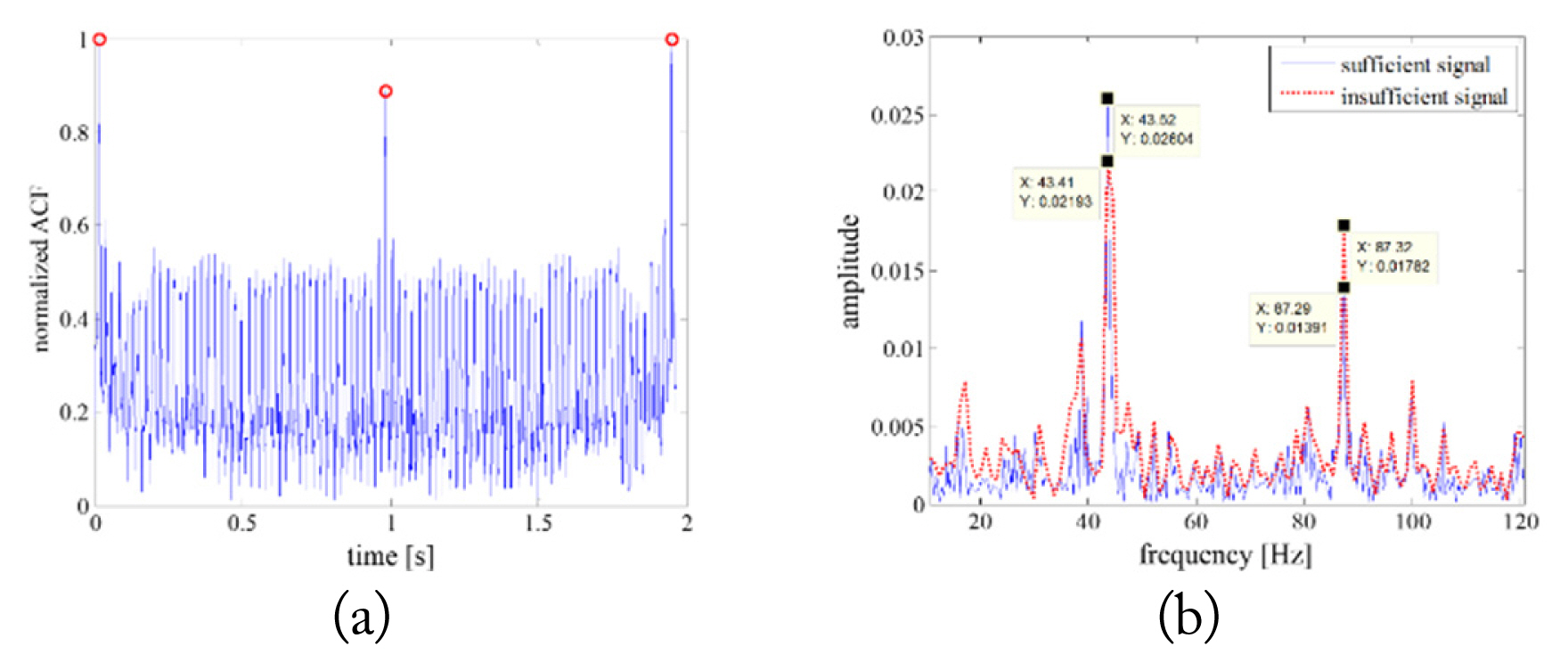
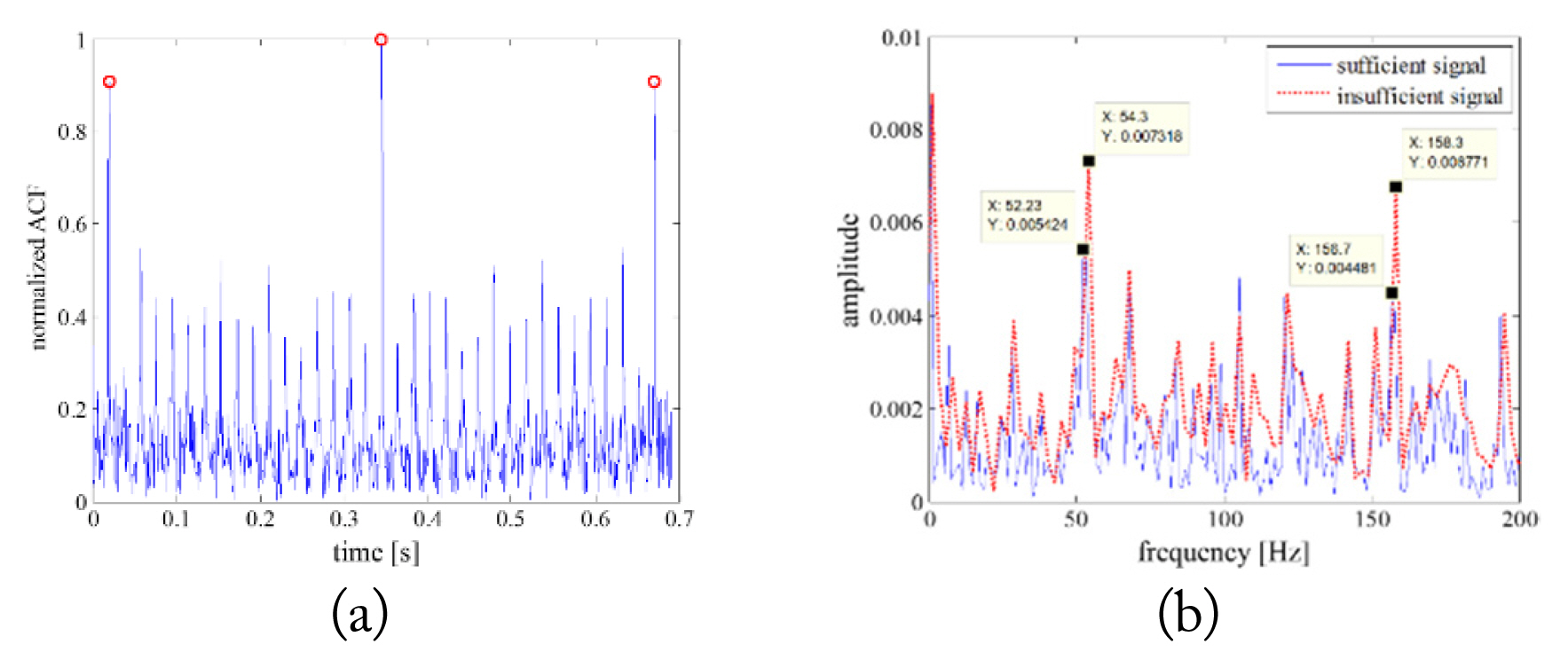
1. T Kirubarajan, Y Bar-Shalom, WD Blair, and GA Watson, "IMMPDAF for radar management and tracking benchmark with ECM,"
IEEE Transactions on Aerospace and Electronic Systems, vol. 34, no. 4, pp. 1115–1134, 1998.

2. AO Hero and D Cochran, "Sensor management: past, present, and future,"
IEEE Sensors Journal, vol. 11, no. 12, pp. 3064–3075, 2011.

3. AB Charlish, "Autonomous agents for multi-function radar resource management," Ph.D dissertation, University College London. London, UK, 2011.
4. A Charlish, K Woodbridge, and H Griffiths, "Agent based multifunction radar surveillance control," In:
Proceedings of 2011 IEEE RadarCon (RADAR); Kansas City, MO, 2011, pp 824–829.

5. VC Chen and H Ling, Time-Frequency Transforms for Radar Imaging and Signal Analysis. Norwood, MA: Artech House, 2002.
6. VC Chen, F Li, SS Ho, and H Wechsler, "Micro-Doppler effect in radar: phenomenon, model, and simulation study,"
IEEE Transactions on Aerospace and Electronic Systems, vol. 42, no. 1, pp. 2–21, 2006.

7. VC Chen, WJ Miceli, and B Himed, "Micro-Doppler analysis in ISAR-review and perspectives," In: Proceedings of 2009 International Radar Conference: Surveillance for a Safer World (RADAR); Bordeaux, France, 2009, pp 1–6.
8. P Tait, Introduction to Radar Target Recognition. Herts, UK: Institute of Electrical Engineering, 2005.
9. WY Yang, HJ Kim, JH Park, JW Bae, CH Kim, and NH Myung, "Effective reconstruction of insufficient JEM signals based on the CS method,"
Journal of Electromagnetic Waves and Applications, vol. 29, no. 6, pp. 807–818, 2015.

10. JH Park, H Lim, and NH Myung, "Modified Hilbert-Huang transform and its application to measured micro Doppler signatures from realistic jet engine models,"
Progress In Electromagnetics Research, vol. 126, pp. 255–268, 2012.

11. MR Bell and RA Grubbs, "JEM modeling and measurement for radar target identification,"
IEEE Transactions on Aerospace and Electronic Systems, vol. 29, no. 1, pp. 73–87, 1993.

12. H Lim, JH Park, JH Yoo, CH Kim, KI Kwon, and NH Myung, "Joint time-frequency analysis of radar micro-Doppler signatures from aircraft engine models,"
Journal of Electromagnetic Waves and Applications, vol. 25, no. 8–9, pp. 1069–1080, 2011.

13. YW Yong, PJ Hoon, KS Cheol, and MN Hoon, "Automatic feature extraction from jet engine modulation signals based on an image processing method,"
IET Radar, Sonar & Navigation, vol. 9, no. 7, pp. 783–789, 2015.

14. JH Park and NH Myung, "Effective reconstruction of the rotation-induced micro-Doppler from a noise-corrupted signature,"
Progress In Electromagnetics Research, vol. 138, pp. 499–518, 2013.

15. X Bai, M Xing, F Zhou, G Lu, and Z Bao, "Imaging of micromotion targets with rotating parts based on empirical-mode decomposition,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 46, no. 11, pp. 3514–3523, 2008.

16. R Yan and RX Gao, "A tour of the tour of the Hilbert-Huang transform: an empirical tool for signal analysis,"
IEEE Instrumentation & Measurement Magazine, vol. 10, no. 5, pp. 40–45, 2007.

17. I Mostafanezhad, O Boric-Lubecke, V Lubecke, and DP Mandic, "Application of empirical mode decomposition in removing fidgeting interference in Doppler radar life signs monitoring devices," In:
Proceedings of 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society; Minneapolis, MN, 2009, pp 340–343.

18. C Cai, W Liu, JS Fu, and Y Lu, "Radar micro-Doppler signature analysis with HHT,"
IEEE Transactions on Aerospace and Electronic Systems, vol. 46, no. 2, pp. 929–938, 2010.

19. H Lim, JH Yoo, CH Kim, KI Kwon, and NH Myung, "Radar cross section measurements of a realistic jet engine structure with rotating parts,"
Journal of Electromagnetic Waves and Applications, vol. 25, no. 7, pp. 999–1008, 2011.

20. WY Yang, JH Park, JW Bae, NH Myung, and CH Kim, "Automatic algorithm for estimating the jet engine blade number from the radar target signature of aircraft targets,"
IEEE Aerospace and Electronic Systems Magazine, vol. 30, no. 7, pp. 18–29, 2015.