A Novel Automatic Algorithm for Estimating the Jet Engine Blade Number of Insufficient JEM Signals
Article information
Abstract
One of the major issues in multifunction radars is time resource allocation to maximize the radar’s ability. If jet engine modulation (JEM) is more efficiently performed in an insufficient dwell-time environment, the remaining time can be allocated for other tasks. This study presents a novel automatic algorithm for estimating the jet engine blade number of insufficient JEM signals. We employed a harmonic selection rule and a modified empirical mode decomposition (EMD) with an adaptive low-pass filtering. For a refined autocorrelation waveform, the analysis focuses on a desirable combination of intrinsic mode functions derived from the modified EMD. The approach is significant because it enables reliable estimation despite the insufficient JEM signal. Also, the proposed algorithm is innovative because it uses only the time-domain method, not the frequency-domain method. The application is expected to enhance the efficiency of radar resource management.
I. Introduction
Modern multifunction radars can execute numerous disparate tasks, aided by advances in phased array technology that is electronically steered. The typical radar system is required to search a given volume for new targets and detect detailed information from multiple scans of target tracks. Recently, radar systems have also required the performance of sequential functions, such as target identification, classification, and missile guidance. One of the major issues in this multifunction radar system is time resource allocation to maximize the radar’s ability [1–4]. The total radar time budget of one radar system must be shared between each function. The multifunction capability of radar can be enhanced by reducing the operation time of each specific function. In general, target recognition from large data that requires classification is the most time-consuming aspect of measurement and analysis. If target recognition is more efficiently performed in a limited time environment, the remaining time can be allocated for other tasks. Therefore, effective radar resource management can be enabled if the target information is recognized from an insufficient signal.
Among target recognition technologies, jet engine modulation (JEM), which is induced by electromagnetic scattering from a rotating jet engine compressor, is the leading micro-Doppler phenomenon that can impart frequency modulation to the radar target signature [5–7]. The dwell time, also called the measurement time, for the JEM analysis was specified in [8]. The total dwell time must include two rotation cycles of the jet engine compressor to separate the spool line, indicating one rotation frequency. However, if the dwell time is too short, the frequency resolution can be insufficient to separate the spool lines. This causes an incorrect analysis for obtaining the blade number of the jet engine. To overcome this drawback, our algorithm [9] introduced an effective reconstruction of insufficient JEM signals based on the compressed sensing (CS) method. Although a state-of-the-art (SOA) algorithm can achieve an accurate estimation of the blade number for various JEM signals, further enhancements are still needed. First, the CS method cannot be applied in a measured JEM signal for which the spectrum becomes relatively complicated, adding to other nonzero spectral components. Second, the processing time for reconstructing insufficient JEM signals is increased using the linear programming optimization method. Therefore, the algorithm is not a real-time application for non-cooperative target recognition (NCTR).
This study describes a novel automatic algorithm for estimating the jet engine blade number from insufficient JEM signals. Among the various signal decomposition methods, we employed empirical mode decomposition (EMD) because of its data-driven characteristics for which there is no prior assumption on a given input signal [10]. However, EMD is restricted to completely extracting the first harmonic component because of its attributes as a dyadic filter bank. Thus, EMD is modified by inserting an adaptive low-pass filter (LPF) whose cutoff frequency is given as the fundamental chopping frequency (FCF) that can be extracted using automated harmonic selection rules. To obtain the refined autocorrelation function (ACF), the decomposed intrinsic mode functions (IMFs) derived from the modified EMD operation were combined. Finally, the blade number of the jet engine was estimated using the peaks detected from the ACF because the blade number is the number of intervals between the outstanding peaks within the spool peaks. The approach proposed in this study is significant because it enables reliable estimation despite the insufficient JEM signal. In addition, the proposed algorithm is innovative due to its exclusive use in the time-domain method, not the frequency-domain method. Since previous studies have used the spectrum in the frequency domain to estimate the blade number, the proposed algorithm can estimate the blade number using only time-domain methods, such as autocorrelation (AC). The application of the proposed algorithm to insufficient JEM signals demonstrates that the novel automatic algorithm presented in this study improves the accuracy of JEM analysis, and its application is expected to enhance the efficiency of radar resource management.
The rest of the paper is organized as follows. Section II presents the proposed algorithm for estimating the blade number from insufficient JEM signals. In Section III, the measured JEM signals are examined to validate the applicability of the proposed algorithm. Finally, conclusions are discussed in Section IV.
II. Comparison between Sufficient and Insufficient Jem Signals
The blade number can be determined using the blade domain signal, which is converted from the JEM spectrum, and usually has redundant values by rounding off the operation after dividing the real frequencies by the one rotation frequency fR, which is a reciprocal of the spool rate (one rotation period). Thus, to estimate the blade number exactly, the spool rate and JEM spectrum should be clearly obtained from the measured JEM signal.
The spool rate imparts fundamental periodicity to the JEM signals and plays a key role in calculating the blade number. In the general process of estimating the spool rate, the time domain JEM signal is first used to calculate the cepstrum by (1) as
where F, F−1, and x are the Fourier transform operator, inverse Fourier transform operator, and the JEM signal in the time domain, respectively [11]. Since the spool rate determines the fundamental periodicity of the JEM signal, the JEM spectrum comprises spool line spectra, and the cepstrum has an outstanding peak. Then, a certain threshold is determined to designate the time samples as the peak, with cepstrum values above the threshold. Finally, the spool rate is estimated using the detected peak.
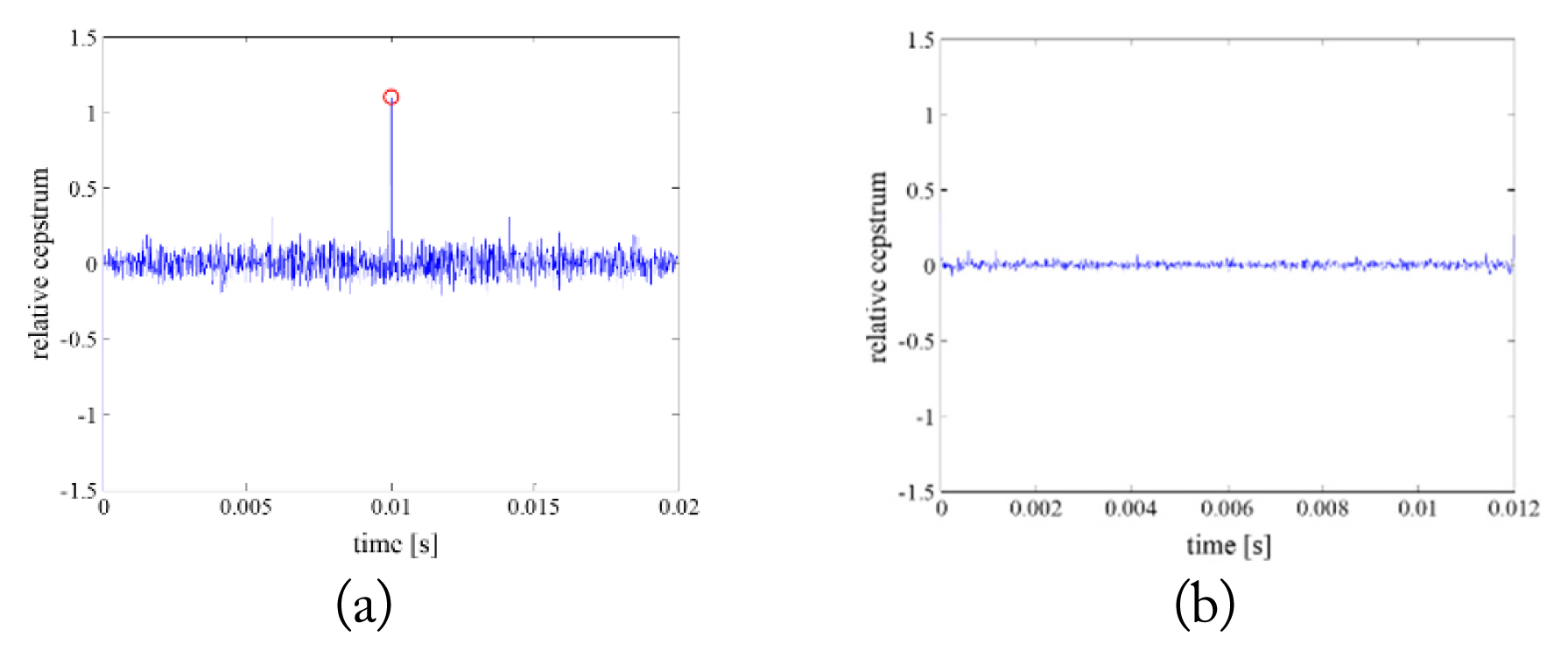
Fig. 1 represents the spool rate estimation using the cepstrum of sufficient and insufficient JEM signals. The JEM signals were obtained from the electromagnetic simulation of realistic jet engine models [12]. Because the rotation speed of a jet engine is 100 Hz, the sufficient time is 20 ms, and the insufficient time is appropriately set to 12 ms. Fig. 1(a) shows the cepstrum of the sufficient JEM signal, and the spool rate was estimated correctly as 100 Hz. In contrast, Fig. 1(b) represents the cepstrum of the insufficient JEM signal, and it is difficult to estimate the spool rate because no peak is related to the spool rate.
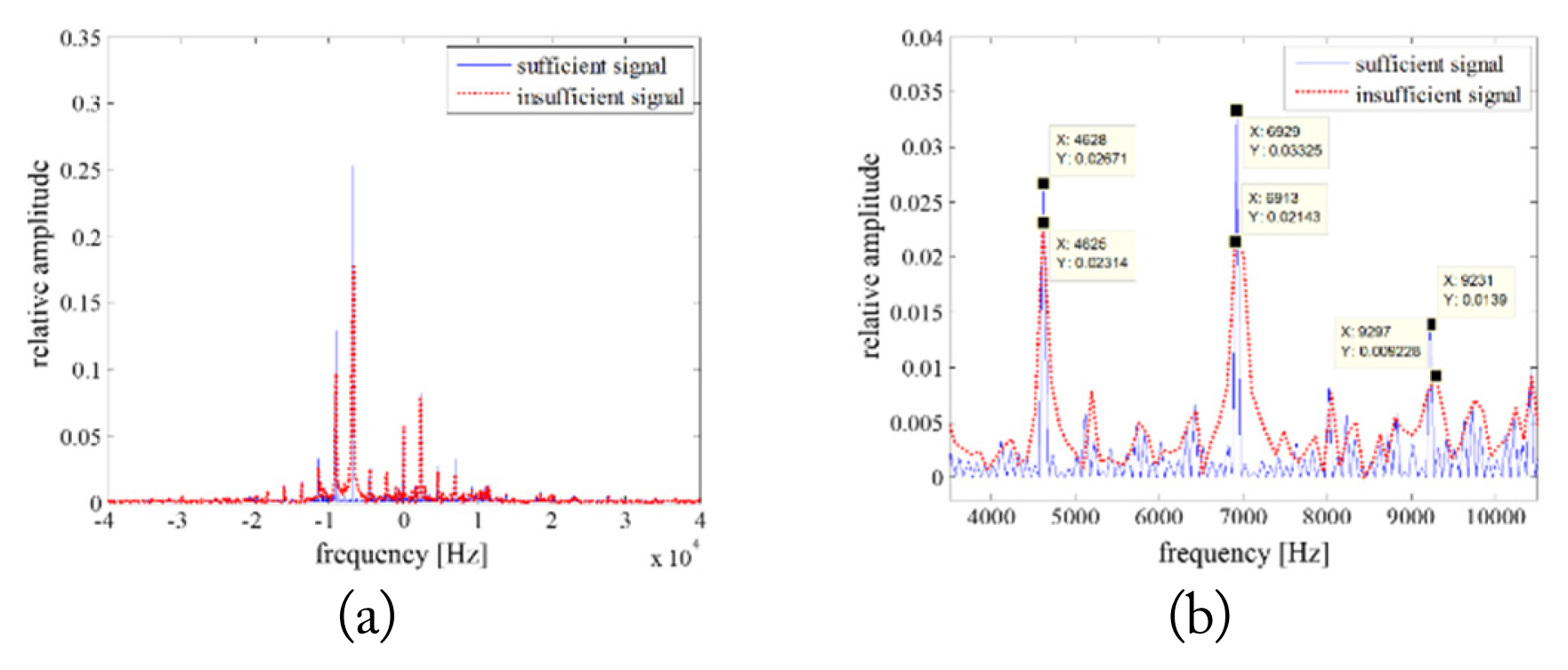
Fig. 2 represents the JEM spectrum of the sufficient and insufficient JEM signals. The JEM spectrum is determined according to the dwell time of a JEM signal. If the dwell time of a JEM signal is too short, the frequency resolution can be insufficient to separate the spool lines. In contrast to the JEM spectrum of the sufficient JEM signal in Fig. 2(a), an insufficient JEM signal cannot obtain accurate spectral lines due to the difference in the frequency resolution marked in Fig. 2(b). Therefore, the insufficient JEM signal cannot estimate the blade number of a jet engine owing to the incorrect estimation of the spool rate and the JEM spectrum.
III. Proposed Algorithm for Estimating the Blade Number
To exactly estimate the blade number for various JEM signals, it is necessary to obtain an accurate spool rate and JEM spectrum with sufficient frequency resolution. As mentioned in Section II-1, however, JEM signals with insufficient time cannot accurately yield the spool rate and sufficiently dense frequency resolution. Thus, the blade number is estimated via the following procedures for insufficient JEM signals (also summarized in Fig. 3):

Overall procedures, including key algorithms Steps 1, 2, and 3 for estimating the blade number from insufficient JEM signals.
Step 1. Extraction of the FCF using the harmonic selection rule.
Step 2. Selection of the cutoff of the preprocessing LPF as the FCF.
Step 3. Decomposition of the signal filtered by the LPF into a finite number of IMFs using EMD.
Step 4. Application of the ACF to the desired combination of extracted IMFs to obtain a refined AC waveform.
Step 5. Acquisition of the blade number using the detected peaks of the ACF.
In Step 1, the analysis focused on the extraction of the fundamental chopping harmonic, which is the key role of the proposed algorithm. The fundamental chopping harmonic has a larger amplitude than other JEM line spectra in many cases of measured JEM signals [13, 14], but this is not always true; thus, the harmonic selection rule is proposed to extract the fundamental chopping harmonic frequency. First, the original frequency domain signals are changed into integer values by a rounding-off operation, as shown in Fig. 4(b). Among the frequency domain signals, the peaks that are near zero Doppler are removed because it is not the frequency domain signal that we are interested in. In addition, when the harmonics are more than the spectral line of zero Doppler, the corresponding frequency domain signals are eliminated. From the remaining frequency domain signal, only 20 harmonic components (line spectra) are empirically extracted in descending order of spectral amplitude, as shown in Fig. 4(c). Then, the preliminary candidate of the FCF is obtained based on the maximum spectral line. If there is no half frequency harmonic, the preliminary candidate is directly designated as the FCF. However, when there is a half, third, or fifth frequency harmonic, the corresponding frequency is selected as the FCF. As shown in Fig. 4(d), the FCF can be extracted using these harmonic selection rules.
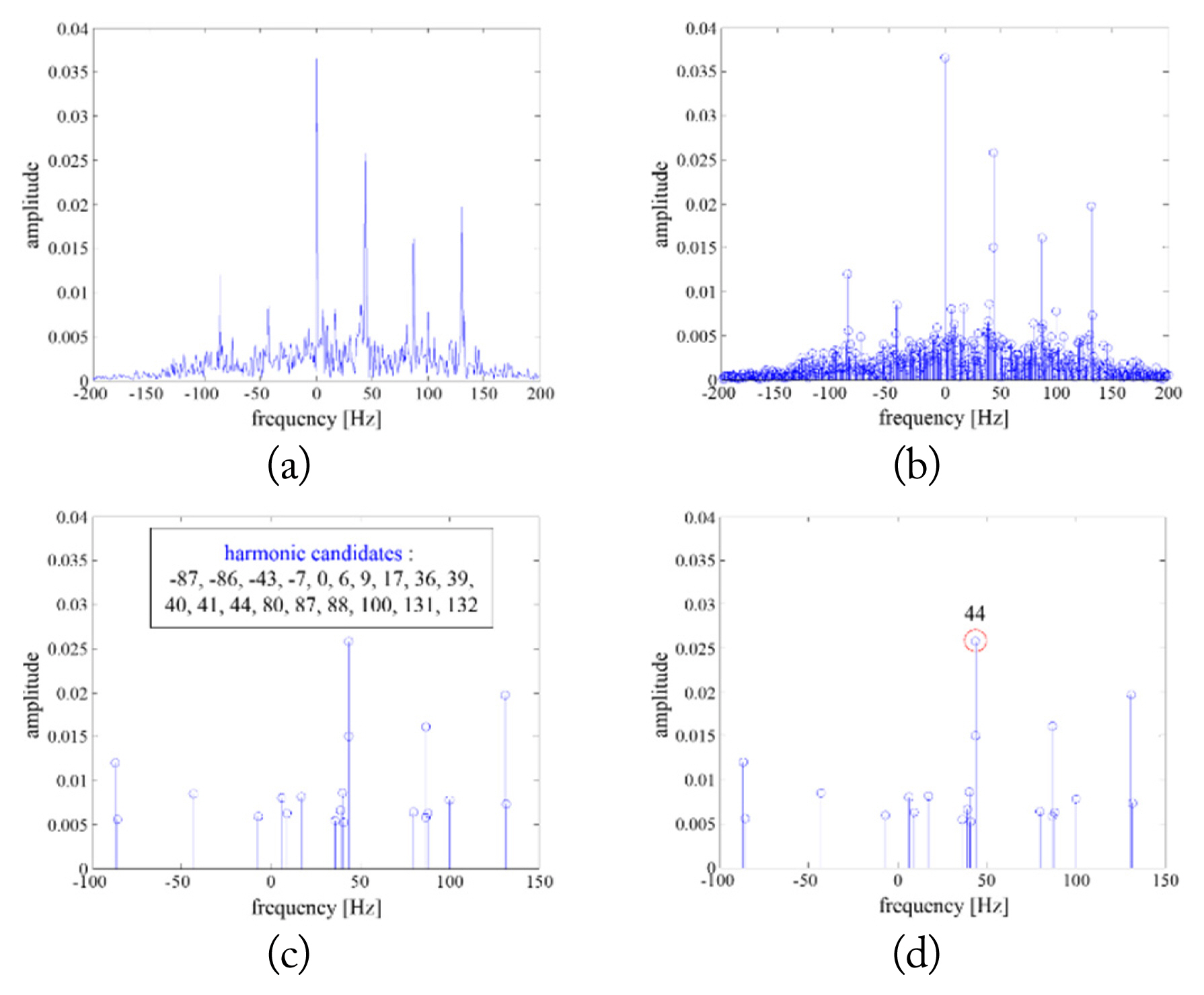
Overall procedures for extracting the fundamental chopping frequency: (a) original JEM spectrum with a sparse frequency resolution, (b) JEM spectrum after applying (a) to a round-off operation, (c) JEM spectrum based on the higher amplitude, and (d) FCF extraction using the harmonic selection rule.
In Step 2, the LPF whose cutoff frequency is selected as the FCF is inserted as a preprocessor of EMD to supplement its filter bank property and completely extract the first chopping harmonic component. According to [13], the fundamental chopping harmonic plays an important role in reconstructing noisy and insufficient JEM signals, and the decomposition of the JEM signals is conducted based on the extraction of this spectral component, which is directly related to the blade number in the first rotor stage. The cutoff frequency of the LPF is determined to be the FCF extracted from Step 1. Fig. 5(b) presents the resultant spectrum after applying the original JEM spectrum of Fig. 5(a) to the preprocessing LPF.
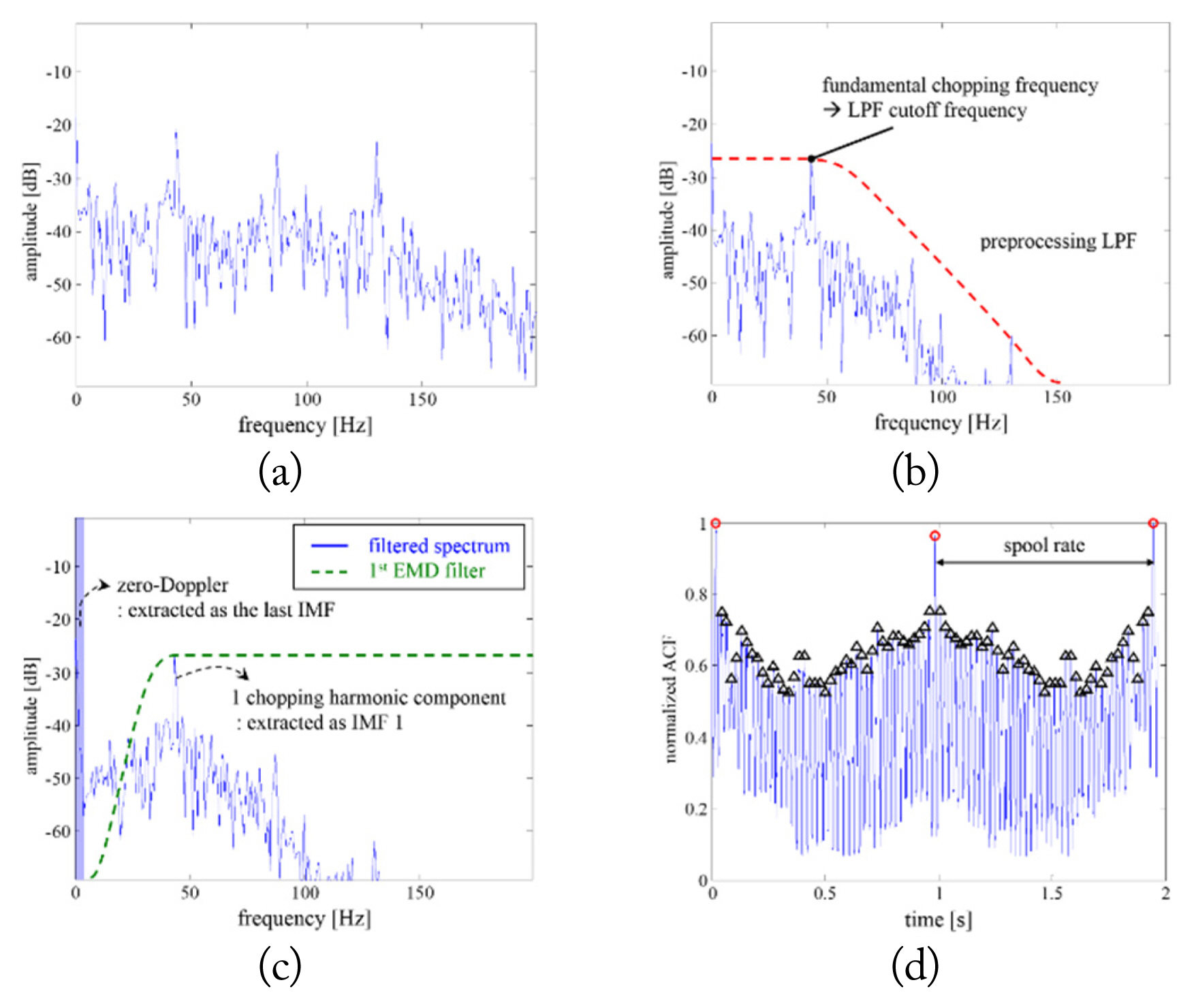
Overall procedures for reconstructing an insufficient JEM signal: (a) insufficient JEM spectrum, (b) JEM spectrum after applying (a) to the LPF, (c) JEM spectrum of IMF 1 combined with the last IMF, and (d) blade number extraction from the ACF result.
In Step 3, EMD, a data-driven decomposition method for nonlinear and non-stationary signals [15–17], is applied to the signal derived from Step 2. Due to preprocessing filtering, the first chopping harmonic component is automatically assigned to the EMD filter of the number 1. Also, IMF 1 has a center frequency following the cutoff frequency and contains the first chopping harmonic, which denotes an effective JEM component [10, 18]. Since the EMD filter of number 1 operates as a high-pass filter, EMD combined with the LPF behaves equivalently like a band-pass filter with the same center frequency as the FCF. In addition, the last IMF with the slowest oscillatory mode corresponds to the zero-Doppler component and is also required to obtain the well-presented ACF in the next step. Fig. 5(c) shows the spectrum of IMF 1 combined with the last IMF resulting from the modified EMD operation to the filtered spectrum.
In Step 4, the ACF in the time domain is utilized to observe the correlation properties of the combined insufficient JEM signal. The JEM AC data are obtained using an unbiased AC sequence estimation and normalization by (2) as
where z is the combined complex JEM data in the time domain, and N is the total length of the JEM data [11]. The ACF is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise. In this study, the JEM ACF yields a refined AC waveform by applying it to the combined signal with IMF 1 and the last IMF, which denotes the first harmonic component and the zero-Doppler component, respectively. This refined AC waveform makes it easy to automatically extract the blade number on the jet engine via detected peaks within the outstanding peaks, which will be presented in Step 5. Fig. 6 shows the AC waveform of the measured raw JEM signal with insufficient dwell time and the reconstructed JEM signal with IMF 1, respectively. The AC waveform of the insufficient JEM signal has ambiguous peaks from the complicated waveform. Unlike the AC waveform shown in Fig. 6, useful information can now be obtained from the well-presented AC waveform shown in Fig. 5(d).
In Step 5, the blade number is estimated from a refined AC waveform. As shown in Figs. 5(d) and 6, the JEM AC waveform has generally outstanding peaks uniformly spaced at every spool rate because the outstanding peaks come from a full rotation of the rotor. In addition, regular waveform within the outstanding peak can be additionally obtained using the combined signal that contains the fundamental chopping harmonic, which is directly related to the chopping rate, the period of a jet engine blade moving to its adjacent position. Because the interval between adjacent peaks within outstanding peaks denotes the chopping rate, the blade number is finally determined by the number of detected peaks of the regular waveform within the spool rate. Therefore, for the example case exhibited in Fig. 5(d), the blade number can be estimated as 42 using the proposed algorithm.
The proposed algorithm enables blade number extraction despite the insufficient JEM signal. In addition, the proposed algorithm is innovative because it uses only the ACF, which is a time-domain method, not a frequency-domain method. Although the spectrum of the insufficient JEM signal lacks a sufficiently dense frequency resolution to extract the blade number, the blade number can be estimated using the reconstructed JEM signal and the time-domain method.
IV. Verification with Measured Jem Signals
In this section, the measured JEM signals are examined to verify the proposed algorithm. In [19], experimental jet engine models were fabricated, and measurements were conducted using the instrumentation radar system for various aspect angles and engine rotation speeds. A rotating part and the whole shape of the fabricated jet engine models are shown in Fig. 7. The structural information on the jet engine models and measurement parameters is given in Table 1. For a fixed radar aspect angle of 50°, we selected two signals from different engine types with different rotating speeds.
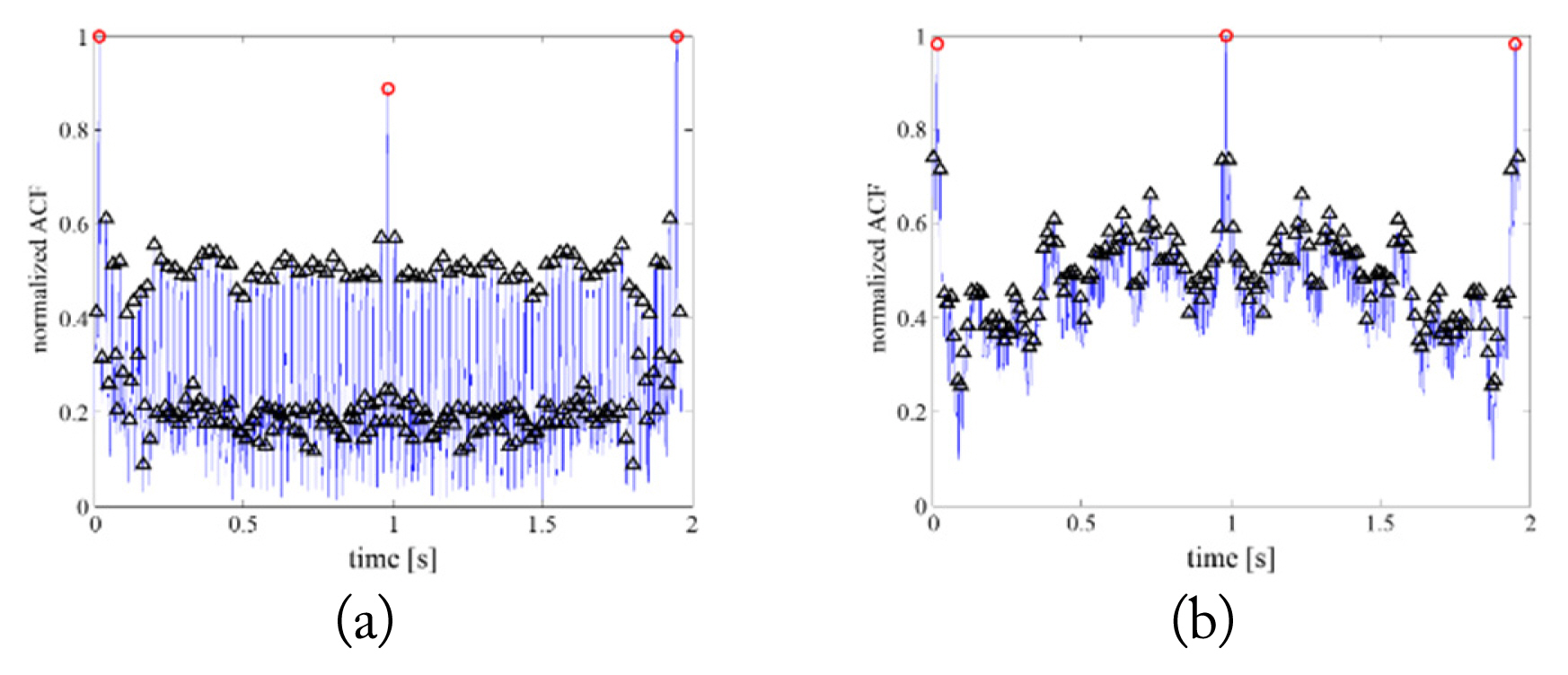
Fig. 8 represents the ACF result and JEM spectrum from a type A engine before applying the proposed algorithm to the insufficient signal. Note that the insufficient dwell time was chosen as 1.1 seconds, and the sufficient dwell time was set as 2 seconds because the rotation speed is 1 Hz (= 60.1 rpm). Although the accurate spool rate was obtained from the outstanding spool peaks shown in Fig. 8(a), we cannot obtain the information within the spool rate from the ambiguous peaks. In addition, it is difficult to obtain accurate spectral lines due to the difference in the frequency resolution marked in Fig. 8(b). Therefore, the blade number on the jet engine was erroneously estimated, as summarized in Table 2. Note that the automatic extraction method [20] can estimate the blade number using the divisor-multiplier rule and the scoring concept in JEM spectral analysis.
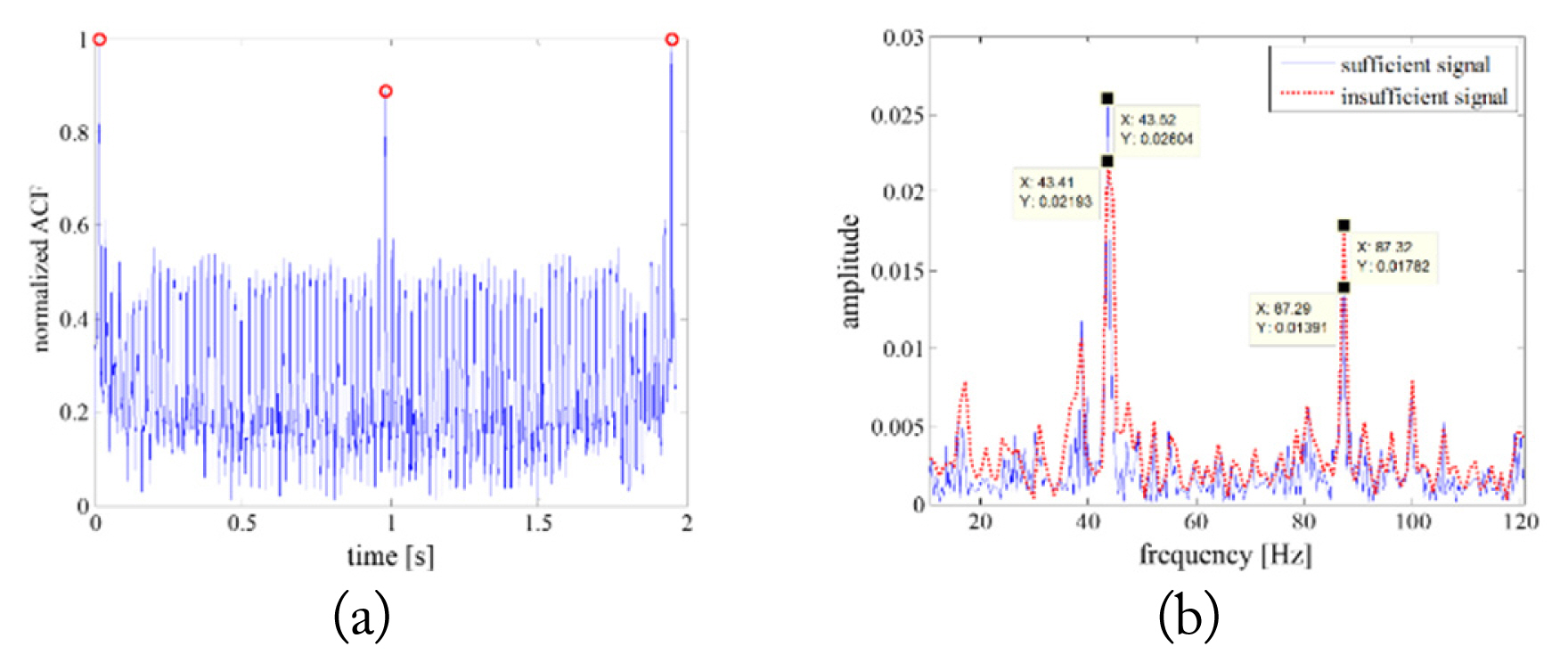
Results of an insufficient JEM signal from a type A engine rotating in the range of 60.1 rpm: (a) ACF and (b) JEM spectrum.
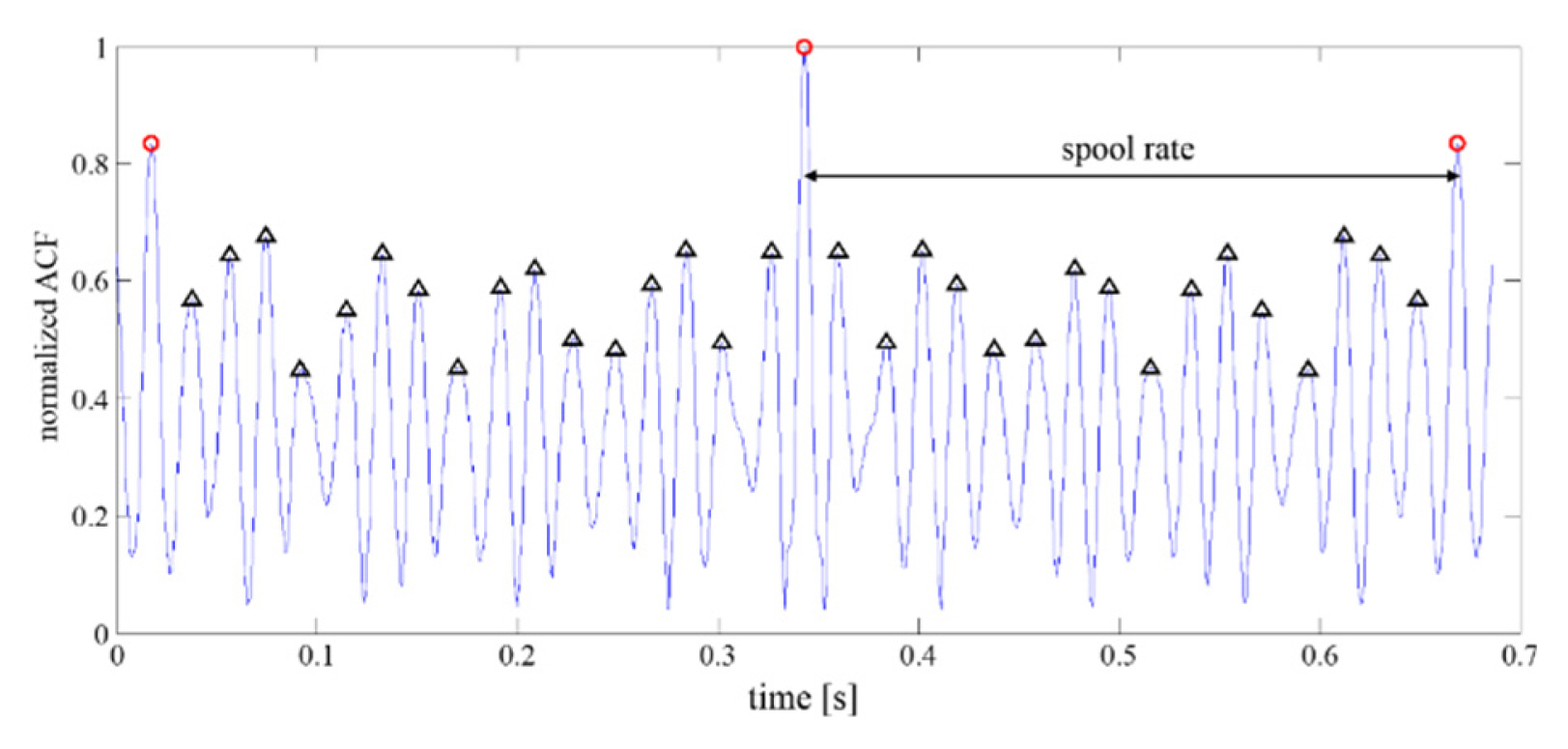
Fig. 9 shows the ACF result from a type A engine after processing with the proposed algorithm. As described previously, the ACF was applied to IMF 1 combined with the last IMF (IMF 11 in this case) and can exhibit a periodic AC waveform. The spool rate, the full rotation period, can be found using the periodically repeating partial group, as marked in the ACF result. The chopping rate, the period when a blade moves to its adjacent position, can also be estimated from peaks, as marked with the triangle. Using the detected peaks within the spool rate, the blade number at the first rotor can be obtained, as summarized in Table 2. From Table 2, we can observe that the blade number can be exactly estimated as 42.
Figs. 10 and 11 exhibit the results of a type B engine before and after applying the proposed algorithm to the insufficient signal, respectively. For this type, the insufficient and sufficient dwell times and the last IMF were chosen as 0.37 seconds, 0.67 seconds, and IMF 10, respectively. Although we cannot obtain useful information on the jet engine model with the insufficient JEM signal shown in Fig. 10, the refined ACF result can be obtained by applying the proposed algorithm. With the refined ACF result, we can estimate the blade number at the first rotor from the peak information within the spool rate in Fig. 11. The jet engine number and processing time required by applying the existing method and the proposed method are summarized in Tables 2 and 3. Note that the average processing time was evaluated by MATLAB on a laptop with a 2.90 GHz Intel Core i7-7500U and 16 GB of RAM. This result shows a different result from that verified through the simulation signal obtained by the shooting and bouncing rays (SBR) method—existing and proposed algorithms accurately estimate the number of engine blades for the simulated signals. The method in [20], which is an automated algorithm that enables fast information acquisition for only a sufficient JEM signal, cannot obtain accurate jet engine information. The only existing algorithm that can be applied to the insufficient signal proposed in [9] can accurately acquire jet engine information, but it takes about 324 times longer than the proposed method because it uses the CS method, which includes an optimization process to restore the JEM signal. However, the proposed algorithm shows a good match with the real parameters. Consequently, the proposed algorithm facilitates a robust and fast estimation of the blade number.
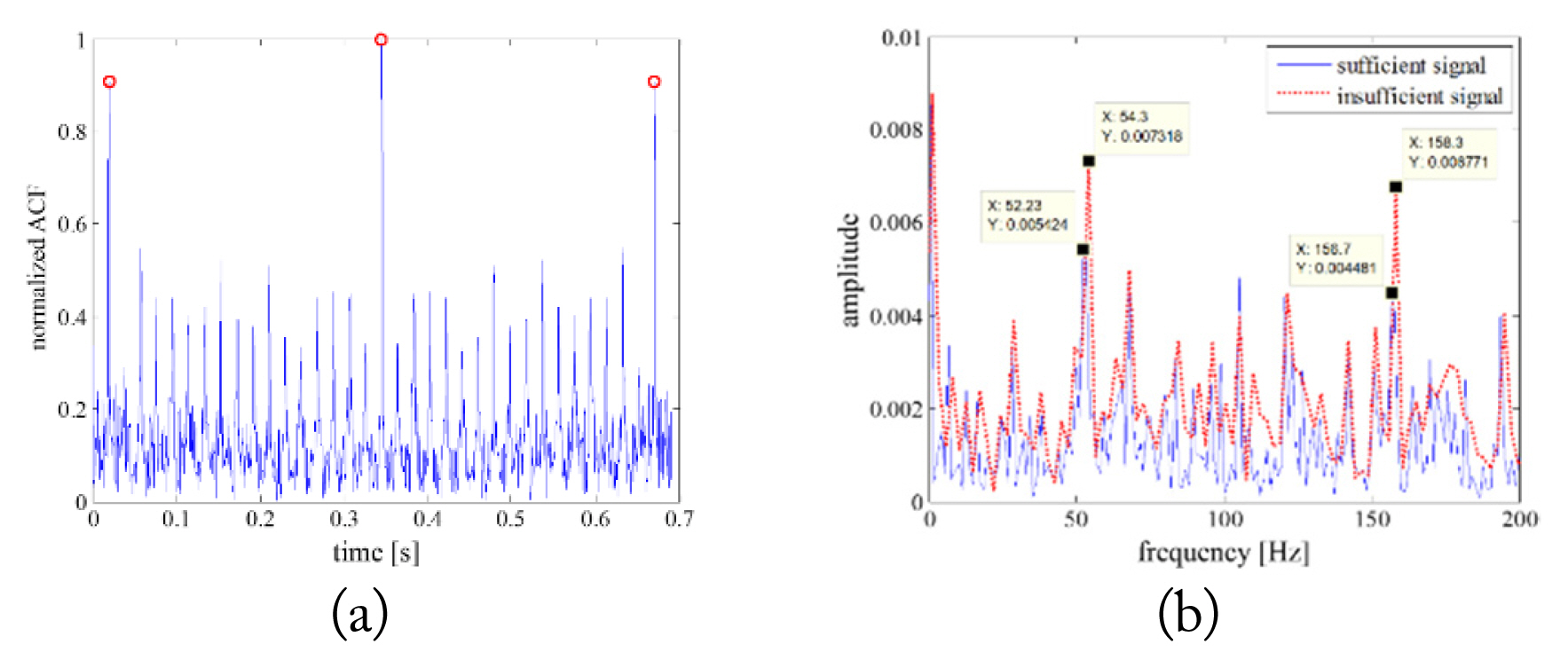
Results of insufficient JEM signal from a type B engine rotating in the range of 180.7 rpm: (a) ACF and (b) JEM spectrum.
Application results with the measured JEM signals demonstrate that the proposed algorithm is effective in accurately and efficiently estimating jet engine features from insufficient JEM signal. Particularly, as shown in the verification process, it is possible to extract the blade number with a dwell time of 1.1 seconds less than the dwell time of 2 seconds required for the information extraction. It is very effective because the radar can allocate about 45% of the remaining time to other functions, such as searching and tracking.
V. Conclusion
The multifunction operation of radar requires finite radar resources to be distributed among various tasks. If JEM is more efficiently performed in an insufficient dwell time environment, the remaining time can be allocated for other tasks. In this study, we proposed a novel automatic algorithm for estimating the jet engine blade number of insufficient JEM signals. The application of the EMD combined with the LPF effectively extracted IMF 1 and the last IMF containing the FCF and zero-Doppler. The blade number of the jet engine was estimated using the peaks detected from the ACF because the blade number is the number of intervals between the outstanding peaks within the spool peaks. Consequently, the proposed algorithm significantly improved the accuracy of JEM analysis and is novel and innovative due to its exclusive use in the time-domain method, not the frequency-domain method. Furthermore, the proposed algorithm is expected to be effective from the perspective of radar resource management. In the future, the proposed algorithm will be applied to various JEM signals received from a jet engine mounted on an actual aircraft and verified.
References
Biography

Woo-Yong Yang received a B.S. degree in electronic engineering from Sogang University in 2005 and an M.S. degree from the School of Electrical Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea, in 2007, and the Ph.D. degree from the School of Electrical Engineering, KAIST, in 2015. He is currently a chief engineer with the UK Office, Hanwha Systems, Seoul, South Korea. His research interests are radar system design, antenna and radar signal processing, and NCTR algorithm analysis.

Dal-Jae Yun received a B.S. degree in electrical engineering from Hanyang University, Seoul, Korea, in 2012. He received a Ph.D. degree in electrical engineering from KAIST, Daejeon, Korea, in 2018. He is currently a senior researcher at the Korea Research Institute of Standards and Science (KRISS). His current research interests include electromagnetic scattering analysis and inverse synthetic aperture radar imaging algorithms.

Dong-Wook Seo received a B.S. degree in electrical engineering from Kyungpook National University, Daegu, South Korea, in 2003, and M.S. and Ph.D. degrees in electrical engineering from Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea, in 2005 and 2011, respectively. He was a senior researcher for the Defense Agency for Technology and Quality (DTaQ), Daegu, from 2011 to 2012. From 2012 to 2017, he was a senior researcher at the Electronics and Telecommunications Research Institute (ETRI), Daegu. Since September 2017, he has been a faculty member of the Division of Electronics and Electrical Information Engineering, Korea Maritime and Ocean University (KMOU), Busan, South Korea, where he is currently an associate professor. His current research interests include numerical techniques in the areas of electromagnetics, radar cross-section analysis, wireless power transfer, and radar systems.