A Measurement Image Translation-Automatic Target Recognition Technique Based on CycleGAN with SAR Simulation DB

Seung Mo Seo; Yeoreum Choi; Ho Lim; Dae-Young Chae

doi:10.26866/jees.2022.3.r.94

J. Electromagn. Eng. Sci > Volume 22(3); 2022 > Article

Seo, Choi, Lim, and Chae: A Measurement Image Translation-Automatic Target Recognition Technique Based on CycleGAN with SAR Simulation DB

Regular Paper

Journal of Electromagnetic Engineering and Science 2022;22(3):326-334.

Published online: May 31, 2022

DOI: https://doi.org/10.26866/jees.2022.3.r.94

A Measurement Image Translation-Automatic Target Recognition Technique Based on CycleGAN with SAR Simulation DB

Seung Mo Seo^*, Yeoreum Choi, Ho Lim, Dae-Young Chae

Defense Artificial Intelligence Technology Center (DAITC), Agency for Defense Development, Daejeon, Korea

^*Corresponding Author: Seung Mo Seo (e-mail: seungmos@gmail.com)

Received July 10, 2021 Revised August 12, 2021 Accepted August 16, 2021

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The proposed approach achieves the reliable accuracy of synthetic aperture radar-automatic target recognition (SAR-ATR) with a simulation database. The simulation images of targets-of-interest are generated from inverse SAR using high-frequency techniques. A measurement image translation-automatic target recognition (MIT-ATR) uses two deep learning networks. The unique feature of the MIT-ATR is that the measurement images are translated to the simulation-like images by cycle generative adversarial network (CycleGAN). CycleGAN does not need to have a dataset of paired images between the measurement and simulation images. The generated simulation-like images are used as the inputs of the Visual Geometry Group (VGG) network. The VGG network is trained on a simulation database with a softmax layer of multi-classes. Five classes, including a T-72 tank, are considered in the numerical experiments. The images of each class are simulated at all azimuth angles, but the elevation angles range from 6° to 30°. The accuracy of the proposed approach is 63% better than that of the traditional method with only the VGG network. The simulation database could definitely supplement the lack of measurement data. The accuracy of MIT-ATR is properly handled by CycleGAN and the VGG network.

Keywords: Automatic Target Recognition (ATR), Cycle Generative Adversarial Network (CycleGAN), Deep Learning (DL), Inverse Synthetic Aperture Radar (ISAR), Machine Learning (ML), Synthetic Aperture Radar (SAR)

I. Introduction

Synthetic aperture radar (SAR) [1] has been widely developed to obtain high-resolution two-dimensional (2D) images of objects. Usually, optical images are very limited to only day and clear weather conditions. However, SAR images could be obtained in almost any condition, regardless of daylight, cloud coverage, weather, and so on. The SAR system provides a 2D reflectivity map of regions of interest (ROIs) with bright spots from a high backscattered signal. Until recently, it has been impossible for image analysts to process all the collected data from various resources. Due to the rapid growth of such an enormous collection capacity, the demand for automatic target recognition (ATR) has been continuously increasing.

In SAR-ATR [2, 3], it is very important to build a database (DB) of targets of interest (TOIs) from measurement images. However, it is very difficult to construct a measurement DB from various angles. Therefore, it is very hard to recognize the target signature. To overcome this difficulty, the simulation images of TOIs could be generated from inverse SAR (ISAR) [4] to supplement the measurement images.

There is a common procedure for generating simulation images of TOIs. First, the computer-aided design (CAD) model of a target can be generated from a laser scan or indirect information, such as an online CAD model or photos. The accuracy of the CAD model depends on the operating frequency of the SAR system. Second, the radar cross-section (RCS) of the CAD model can be computed using various numerical techniques. In full-wave methods, three main categories, namely, method of moments (MoM) [5], finite element method [6–8], and finite difference time domain (FDTD) [9–12], are very popular in the community of computational electromagnetics. However, these approaches require a lot of numerical complexity of memory and CPU time to solve the problem in the X-band (approximately 10 GHz). To overcome these numerical complexities, fast algorithms, such as the multilevel-fast multipole method (ML-FMM) [13], integral equation-fast Fourier transform (IE-FFT) [14, 15], domain decomposition-finite element method (DD-FEM) [16], and finite difference time domain-message passing interface (FDTD-MPI) [17], have been developed. However, these techniques could still be limited to constructing a simulation DB for target recognition. Therefore, high-frequency techniques [18–20] are very useful and powerful methods, notwithstanding the inaccurate results compared with full-wave methods. Finally, ISAR images can be generated from RCS data using a frequency sweep. Inaccurate modeling and high-frequency techniques should be carefully handled.

Deep learning frameworks, such as TensorFlow [21], PyTorch [22], and others [23–25], have been widely used with GPU-accelerated libraries. Frameworks based on convolutional neural networks (CNN) [26] have been developed and specialized in image recognition and computer vision. The Visual Geometry Group (VGG) network [27] by the University of Oxford has been very popular in its good performance despite its simplicity. The Pix2pix [28] network learns mapping from input images to output images. The network creates a desired image by the conditions of the latent variables. The generative adversarial network (GAN) [29] efficiently learns to generate new images with the same statistics as a training set. The main disadvantage of this technique is that the network should have paired images for the training sets. CycleGAN [30] proposes an image translation technique from a source domain to a target domain without paired sets. In the area of SAR-ATR, deep learning research is continuously increasing. Deep learning research based on CNN [31], faster region-CNN (R-CNN) [32], you only look once version 2 (YOLOv2) [33], etc., has been analyzed, tested, and developed.

This paper proposes a measurement image translation-automatic target recognition (MIT-ATR) method based on CycleGAN with an SAR simulation DB. The uniqueness of the proposed method is that it translates from measurement images to simulation-like images. The main reason for using a simulation DB is that the measurement images are not sufficient at all angles. Therefore, CycleGAN is considered and recommended to supplement measurement images owing to unpaired image-to-image translation. The main difficulty in using a simulation DB is generating images similar to measurements. Conventionally, simulation images are pre-processed by image adjustments, such as an image filter, intensity, histogram statistics, etc. These techniques are very inconvenient and time-consuming processes. The proposed approach is to generate simulation-like images using CycleGAN. The generated images are tested by a VGG neural network. The performance of the proposed approach is much better than that of the VGG.

The outline of the article is organized as follows: Section II provides a description of the MIT-ATR technique, Section III demonstrates the accuracy and performance of the proposed approach, and finally, the paper is concluded in Section IV.

II. A Measurement Image Translation-Automatic Target Recognition Technique

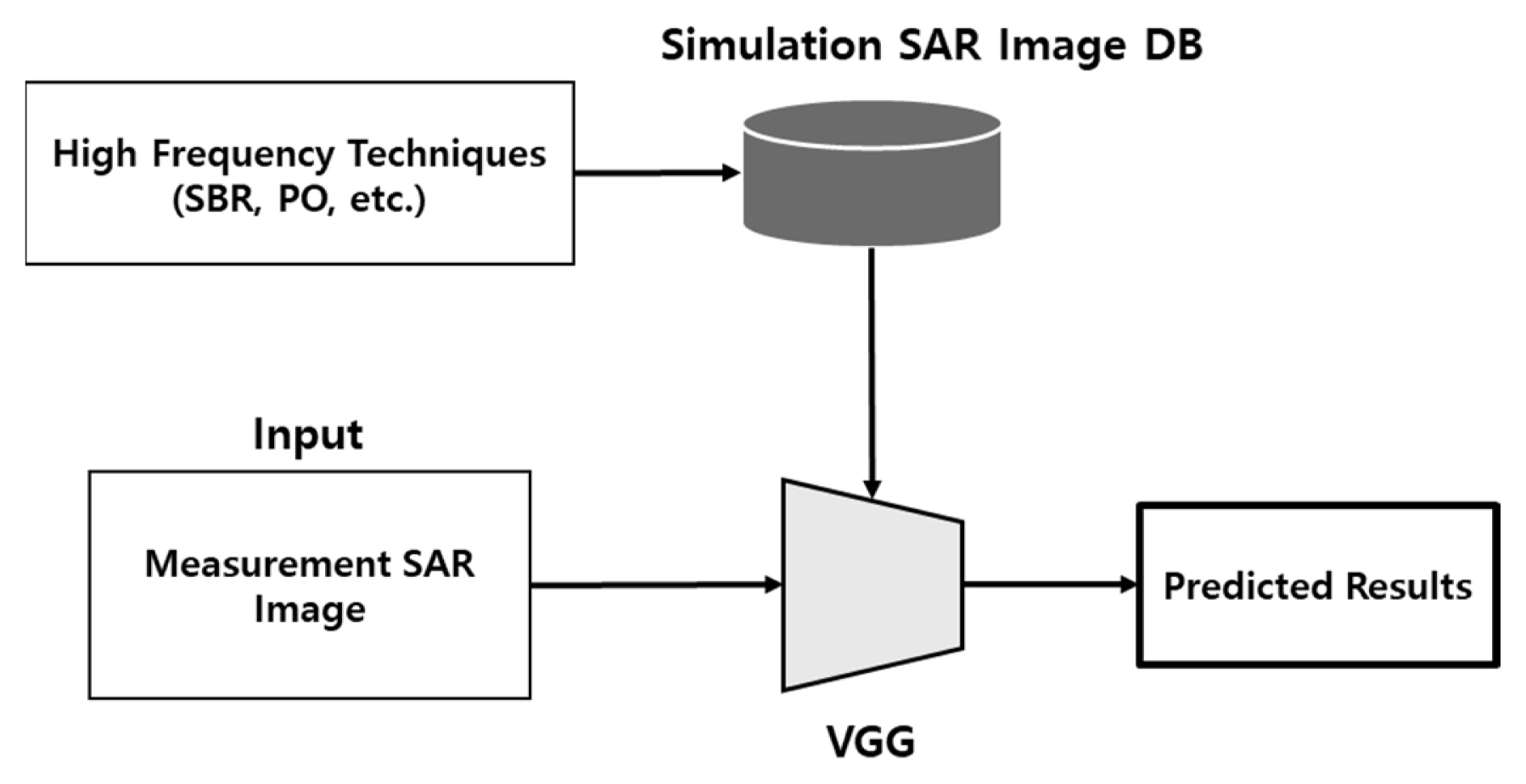
An MIT-ATR technique is proposed to enhance target classification when the simulation DB is available. The proposed approach has two steps. The first step is the translation process through CycleGAN. A measurement image with noise is translated into an image similar to a simulation image generated from a high-frequency technique, such as shooting and bouncing rays (SBR), physical optics (PO), etc. The second step is the classification process through the VGG network. These steps are much better than the VGG network on its own. Fig. 1 shows the conventional target recognition approach. Due to insufficient measurement DB, the simulation DB is used. However, the accuracy of target recognition is extremely limited due to discrepancies between the measurement and simulation images.

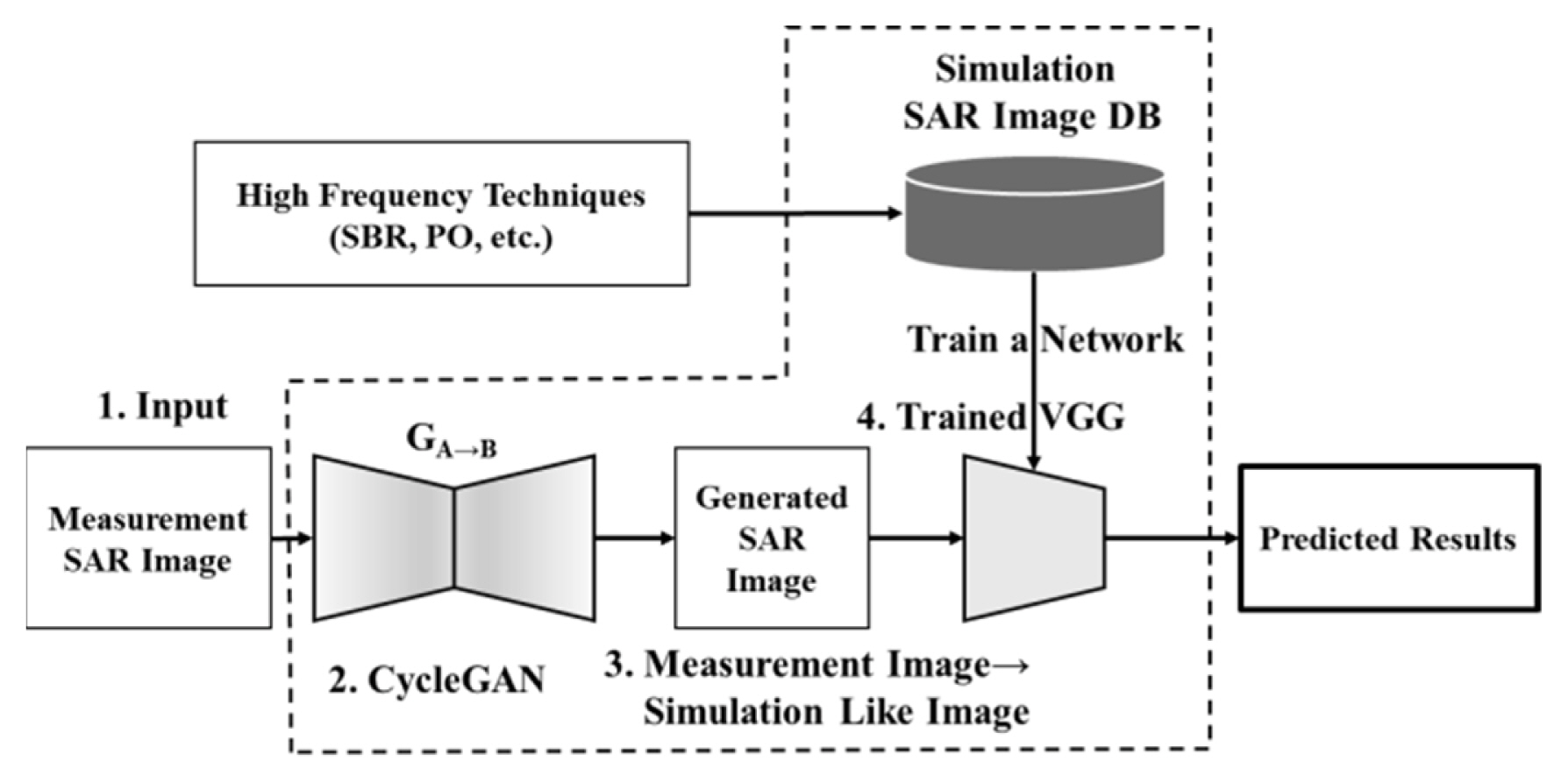
Therefore, an MIT-ATR approach based on the VGG network with the simulation DB is shown in Fig. 2. In the training stage, the measurement images are trained on CycleGAN to construct simulation-like images. On the other hand, the simulation images are trained on the VGG network with the simulation DB due to the lack of measurement data. In the testing stage, the measurement images are translated into simulation-like images. The VGG network trained with the simulation DB classifies the translated images as a softmax function of multiple classes. The main difference between the conventional and proposed approaches is the translation stage from measurement images to simulation-like images.

1. VGG Network based on CNN

In this section, a VGG network based on transfer learning is used for target classification by ImageNet [34]. The VGG16 network is shown in Fig. 3. Originally, the input of VGG16 was a fixed-size 224 × 224 RGB image. In this paper, the size of the input images is a 50 × 50 gray image, which is the maximum size of TOIs. For transfer learning, 50 × 50 SAR images should be resized to fit the input size of VGG16 by bi-cubic interpolation. The resized SAR images train the basic VGG16, which consists of convolutional, max-pooling, fully-connected (FC), and soft-max layers. The convolution filters have 3 × 3 pixel windows. Five max-pooling layers are followed by some of the convolutional layers. Finally, a stack of convolutional and max-pooling layers is followed by three FC layers. The outputs of the softmax layer are the five classes in this paper.

2. Cycle Generative Adversarial Network

The use of a simulation DB could solve the lack of measurement data. However, using only the VGG network does not guarantee the accuracy of the target classification. In this section, CycleGAN is proposed as the pre-processing of the VGG network. A brief objective of CycleGAN is explained. There are two types of losses in CycleGAN. One is the adversarial loss, which is given by:

(1)

minGmaxDYLA(G,DY,X,Y)=Ey~pdata(y)[log DY (y)]+Ex~pdata(x)[log (1-DY(G(x)))]

and

(2)

minFmaxDXLA(F,DX,X,Y)=Ex~pdata(x)[log DX (x)]+Ey~pdata(y)[log (1-DX(F(y)))]

where G and F are mapping functions from one domain X to the other Y and vice versa, respectively. D_X and D_Y are discriminators between translated samples and real samples. X and Y are two domains for measurement and simulation images. x ~ p_data(x) and y ~ p_data(y) are data distributions of two domains, respectively. The key to GAN’s success is the idea of an adversarial loss that forces the generated images to be indistinguishable from real images. The other is cycle consistency loss, which is expressed as follows:

(3)

LCC(G,F)=Ex~pdata(x)[‖F(G(x))-x‖2]+Ey~pdata(y)[‖G(F(y))-y‖2]

where ||·||₂ indicates L₂ norm. Finally, the loss function of CycleGAN is written as follows:

(4)

L(G,F,Dx,Dy)=LA(G,DY,X,Y)+LA(F,DX,X,Y)+λLCC(G,F)

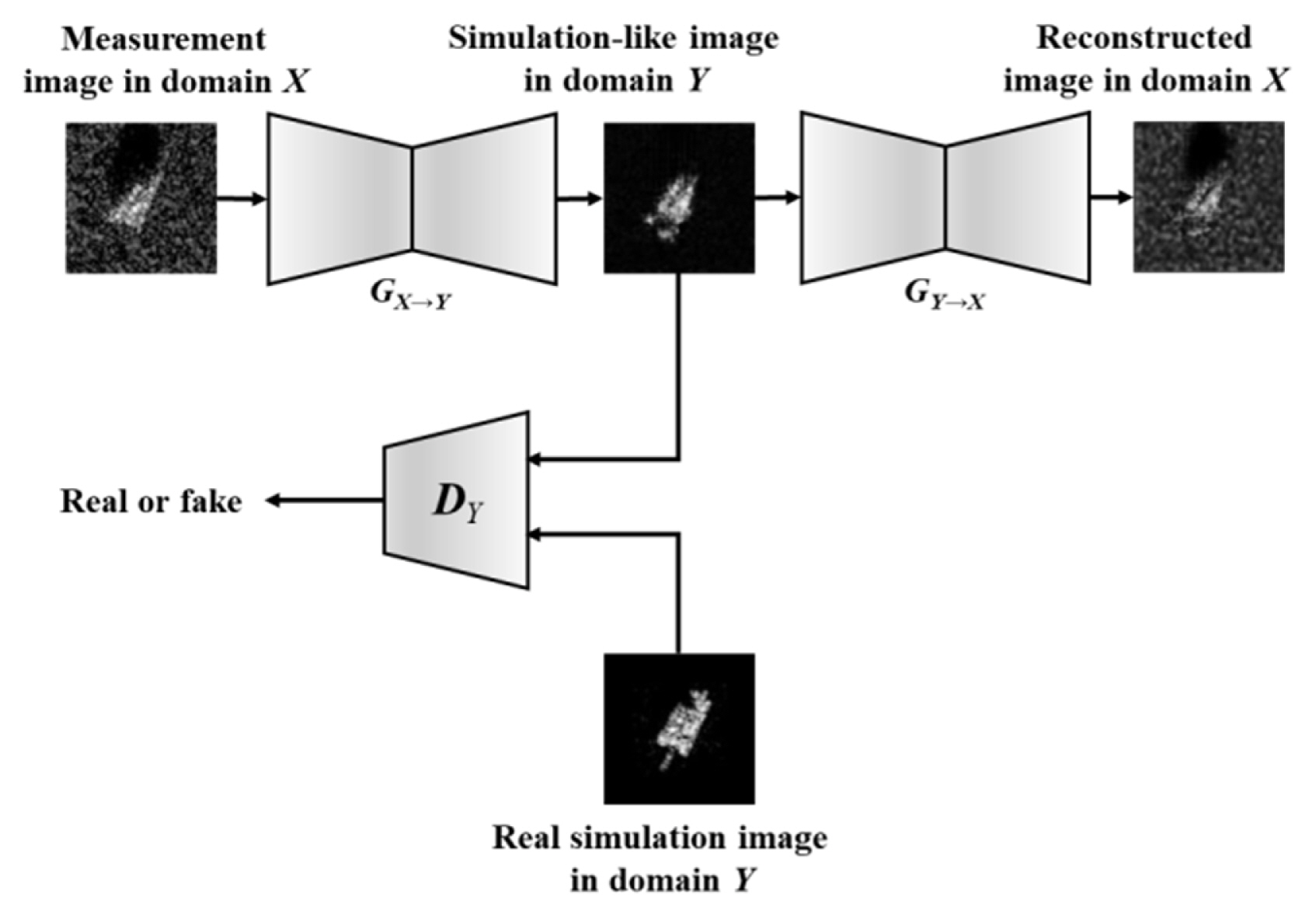
where λ is the weighting constant between two types of losses. In this paper, λ is 10. The details of the implementation of CycleGAN are shown by Zhu [30]. The procedure for CycleGAN is shown in Fig. 4.

The input images could be measurement or simulation images. In this paper, a generator G_X_→_Y translates from a measurement image to a simulation-like image. To ensure cycle consistency, the generated image is translated into a reconstructed image by a generator G_Y_→_X. The cycle consistency loss function tries to minimize the difference between a measurement and a reconstructed image. A discriminator D_Y tries to force the generated images to be indistinguishable from real simulation images. The final goal is to translate measurement images into simulation-like image.

3. A Simulation-Like Image Translation

There are two ways to generate unpaired image-to-image translation using CycleGAN. One approach translates from simulation images to measurement images. The other is the other way around. Fig. 5 shows the 3D CAD model of a T-72 tank. In reality, it is not easy to obtain measurement data without a real model. CAD models from indirect information, such as Internet models or photos, could be required to compensate for insufficient measurement data. From the CAD model, a high-frequency technique can create a simulation SAR image using multiple angle and frequency sweeps. However, the measurement images are quite different from the simulation images. Reducing the discrepancy between two images requires a lot of modification based on indirect information. Due to the advent of CycleGAN, such complicated modifications are not necessary to obtain certain accuracy. However, an accurate matching process between measurement and simulation images should be handled carefully if more accurate results are required.

Fig. 6 shows a comparison of the translation results between a measurement image and a simulation image by CycleGAN. The measurement image is obtained at elevation (EL) = 15° and azimuth (AZ) = 20°. The simulation is obtained from a slightly different angle at EL = 14° and AZ = 20°. The measurement data originated from moving and stationary target acquisition and recognition [35]. The original, translated, and reconstructed images from CycleGAN are described in Fig. 6(a)–6(f). The original measurement image X and simulation image Yare shown in Fig. 6(a) and 6(d), respectively. The translated image G(X) from the mapping G:X→Y is shown in Fig. 6(b). The measurement image is translated into a simulation-like image. The reconstructed image F(G(X)) is shown in Fig. 6(c). The consistence loss function between the original and the reconstructed image is minimized by L₂ norm. The translated image F(Y) from the mapping F:Y→X is shown in Fig. 6(e). For the consistency loss function, the reconstructed image is generated as G(F(Y)) in Fig. 6(f). In this paper, measurement images are used as an input image X. The translated image G(X) is a simulation-like image. To compute the consistency loss, the reconstructed image is generated as F(G(X)). The loss function is rewritten as follows:

(5)

L(G,F,Dx,Dy)=LA(G,DY,X,Y)+λLCC(G,F)

where

(6)

LCC(G,F)=Ex~pdata(x)[‖F(G(x))-x‖2].

The adversarial loss is the same as in Eq. (1). The generator G makes a translated image close to the other domain. The discriminator D_Y compares the generated image G(X) with the original simulation image Y to minimize the adversarial loss.

Fig. 7 shows the original, translated, and reconstructed images at various angles. Fig. 7(a) shows the measurement images at EL = 15°, and AZ = 1°, 43°, and 89°. The simulation images are displayed in Fig. 7(d). Each translated image is shown in Fig. 7(b) and 7(e). Each reconstructed image is displayed in Fig. 7(c) and 7(f). In the proposed approach, the simulation-like images in Fig. 7(b) are tested with the simulation images in Fig. 7(d). The generated images are much more similar than the simulation images. Now, the correlation of the original images is compared with that of the translated images. The values of the correlation between Fig. 7(a) and 7(b) relative to Fig. 7(d) are computed. The coefficient of correlation between the measurement and the simulation images is computed by:

(7)

rMS=cov(M,S)σMσS

where

(8)

cov(M,S)=1N∑i=1N(Mi-μM)(Si-μS),

(9)

σM=1N∑i=1N(Mi-μM)2,

and

(10)

σS=1N∑i=1N(Si-μS)2.

N is the number of pixels for a chip. M_i and S_i are the i^th pixel intensity of the measurement and simulation images, respectively. μ_M and μ_S are the average values of the pixel intensity for the measurement and simulation images, respectively.

The coefficients of correlation between the original and translated measurement images relative to the original simulation images are compared in Table 1. Five pairs of images are shown at different azimuth angles. The average correlation value of the original measurement image relative to the original simulation is 0.5639. However, the average value for the translated measurement images dramatically improved to 0.8076. Overall, the correlation improved to 24%.

III. Numerical Experiments

The proposed approach was compared with the conventional VGG16 network. The proposed algorithm improves the probability of the target classification in five classes when the simulation DB is used. There are two steps: CycleGAN for image translation and the VGG16 network for target classification. The first step generates simulation-like images using CycleGAN. The conventional approach is applied in the second step. Let us experiment with the conventional approach. Table 2 shows the training numbers of the simulation images and the testing numbers of measurement images. The resolution of the images is 30 cm × 30 cm. All SAR images are vertical-vertical (VV) imaginary.

Table 3 shows the confusion matrix of the results of the conventional approach.

Due to the image discrepancy between the testing set and the training set, the accuracy is approximately 15%. The most important fact is that all testing sets are classified as class 2. The backscattered characteristics of class 2 are dominant in all classes. For the improvement of classification, complicated image adjustment and verification processes should be required to reduce the discrepancy between measurement and simulation images. Usually, the measurement data cannot be equally distributed at all angles due to the difficulty of regular acquisition. Therefore, the number of training sets is randomly distributed to each class for an unpaired image-to-image translation. There are two distinct problems. One is to generate simulation-like images. The other is using unbalanced datasets between measurement and simulation images. The key ingredient processor is the unpaired measurement to simulate image translation in the paper. In reality, there is only a small set of measurement data used as a training set. Therefore, the simulation data are randomly extracted in the same number as the measurement data.

The summary of image sets for domain X and Y is shown in Table 4. Based on the proposed algorithm, the results of the target classification are given in Table 5. From the confusion matrix, the accuracy is approximately 80%. Fig. 8 shows the improvement and deterioration of each target class. Overall accuracy improved. The improvement of Class 5 is lower than those of the other classes. The reason is that the data of class 5 and the other classes are obtained from the heterogeneous SAR sensors.

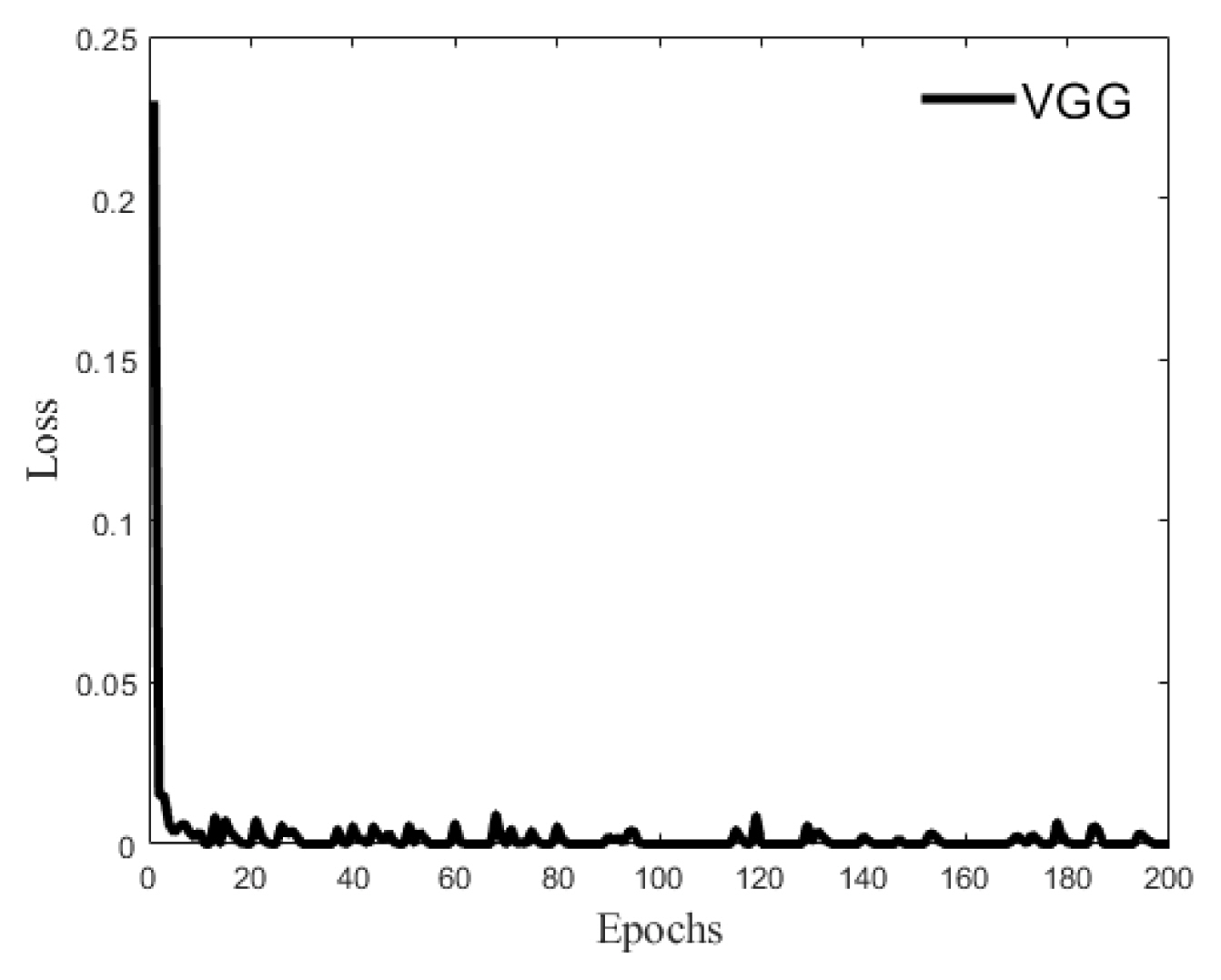
Fig. 9 shows the losses of adversarial and cycle consistency versus epochs. Here, epochs is 200, β₁=0.9, β₂=0.999, the learning rate μ=10⁻⁵, and batch size is 16. In the top figure, the solid line indicates adversarial loss, and the dashed is cycle consistency loss. The bottom figure shows the CycleGAN loss. After 110 epochs, the error converged less than 1.0.

Fig. 10 shows the loss of the VGG network versus epochs. The VGG network uses the object function as an adaptive moment estimation (Adam) [36]. The loss is converged to almost 0 after 10 epochs.

IV. Conclusion

The proposed approach has the unique feature of SAR-ATR by two distinct deep learning networks when the simulation DB is used. The key ingredient of the algorithm is to translate from measurement images to simulation-like images using CycleGAN. From the confusion matrix of five classes, the accuracy is approximately 80%. The accuracy improved by more than 60%. The correlation is close to almost 80%. The measurement images are translated to the images very similarly to the simulation by CycleGAN. The proposed approach demonstrates that the simulation DB can easily be used without any complicated pre-processing techniques.

Fig. 1

Conventional target recognition approach based on VGG network with simulation DB.

Fig. 2

An MIT-ATR approach based on VGG network with simulation DB.

Fig. 3

VGG16 neural network with 50 × 50 × 1 input images.

Fig. 4

Procedure of CycleGAN to generate a simulation-like image.

Fig. 5

The 3D CAD model of a T-72 tank.

Fig. 6

Comparison between a measurement image (at EL = 15° and AZ = 20°) and a simulation one (at EL = 14° and AZ = 20°) for a T-72 tank through CycleGAN: (a) measurement image, (b) a translated image from measurement to simulation-like, (c) a reconstructed image from simulation-like to reconstructed measurement-like, (d) a simulation image, (e) a translated image from simulation to measurement–like, and (f) a reconstructed image from measurement-like to reconstructed simulation-like.

Fig. 7

Original, translated, and reconstructed images at various angles: (a) original measurement images at EL = 15° and AZ = 1°, 43°, and 89°; (b) translated measurement images; (c) reconstructed measurement images; (d) original simulation images at EL = 14° and AZ = 0°, 44°, and 90°; (e) translated simulation images; and (f) reconstructed simulation images.

Fig. 8

Improvement and deterioration of an MIT-ATR technique.

Fig. 9

Adversarial, cycle consistency, and CycleGAN losses versus epoch.

Fig. 10

Loss of VGG versus epochs.

Table 1

Coefficient of correlation between measurement and simulation SAR images

	Simulation SAR image DB at EL = 14° (AZ = 0°, 44°, 90°, 134°, and 178°)

EL = 15° AZ	Original measurement image	Translated measurement image
1°	0.4358	0.8398
43°	0.5736	0.7848
89°	0.7052	0.8432
136°	0.5363	0.7787
180°	0.5687	0.7913
Average	0.5639	0.8076

Table 2

Number of training and testing images

	Number of images

	1	2	3	4	5	Total
Training sets	7,020	7,020	2,340	4,680	2,340	23,400
Testing sets	47	126	259	205	196	833

Table 3

Confusion matrix of the conventional approach

		Predicted

		1	2	3	4	5	Total
Actual	1	0	47	0	0	0	0
	2	0	126	0	0	0	100
	3	0	259	0	0	0	0
	4	0	205	0	0	0	0
	5	0	196	0	0	0	0
	Total	0	833	0	0	0	15.1

The bold diagonal indicates that the prediction and the ground truth are same.

Table 4

Number of measurement images in domain X and simulation images in domain Y for CycleGAN

	Number of images

	1	2	3	4	5	Total
Measurement images in domain X	465	752	803	838	691	3,549
Simulation images in domain Y	465	752	803	838	691	3,549

Table 5

Confusion matrix of the proposed approach

		Predicted

		1	2	3	4	5	Total
Actual	1	42	2	2	1	0	89.4
	2	25	101	0	0	0	80.2
	3	3	0	242	5	9	93.4
	4	9	24	6	160	6	78.1
	5	10	13	35	21	117	59.7
	Total	89	140	285	187	132	79.5

The bold diagonal indicates that the prediction and the ground truth are same.

References

1. WG Carrara, RS Goodman, and RM Majewski, Spotlight Synthetic Aperture Radar: Signal Processing Algorithms. Norwood, MA: Artech House, 1995.

2. P Tait, Introduction to Radar Target Recognition. Stevenage, UK: Institution of Engineering and Technology, 2009.

3. D Blacknell and H Griffiths, Radar Automatic Target Recognition (ATR) and Non-Cooperative Target Recognition (NCTR). Stevenage, UK: Institution of Engineering and Technology, 2013.

4. CC Chen and HC Andrews, "Target-motion-induced radar imaging," IEEE Transactions on Aerospace and Electronic Systems, vol. AES-16, no. 1, pp. 2–14, 1980.

5. RF Harrington, Field Computation by Moment Methods. Piscataway, NJ: Wiley-IEEE Press, 1993.

6. PP Silvester and RL Ferrari, Finite Elements for Electrical Engineers. 3rd ed. New York, NY: Cambridge University Press, 1996.

7. PP Silvester, "Universal finite element matrices for tetrahedra," International Journal for Numerical Methods in Engineering, vol. 18, no. 7, pp. 1055–1061, 1982.

8. ZJ Cendes, "Vector finite elements for electromagnetic field computation," IEEE Transactions on Magnetics, vol. 27, no. 5, pp. 3958–3966, 1991.

9. K Yee, "Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media," IEEE Transactions on Antennas and Propagation, vol. 14, no. 3, pp. 302–307, 1966.

10. A Taflove, "Application of the finite-difference time-domain method to sinusoidal steady-state electromagnetic-penetration problems," IEEE Transactions on Electromagnetic Compatibility, vol. EMC-22, no. 3, pp. 191–202, 1980.

11. G Mur, "Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations," IEEE Transactions on Electromagnetic Compatibility, vol. 23, no. 4, pp. 377–382, 1981.

12. JP Berenger, "A perfectly matched layer for the absorption of electromagnetic waves," Journal of Computational Physics, vol. 114, no. 2, pp. 185–200, 1994.

13. JM Song and WC Chew, "Multilevel fast-multipole algorithm for solving combined field integral equations of electromagnetic scattering," Microwave and Optical Technology Letters, vol. 10, no. 1, pp. 14–19, 1995.

14. SM Seo and JF Lee, "A fast IE-FFT algorithm for solving PEC scattering problems," IEEE Transactions on Magnetics, vol. 41, no. 5, pp. 1476–1479, 2005.

15. SM Seo, CF Wang, and JF Lee, "Analyzing PEC scattering structure using an IE-FFT algorithm," Applied Computational Electromagnetics Society Journal, vol. 24, no. 2, pp. 116–128, 2009.

16. C Farhat, J Mandel, and FX Roux, "Optimal convergence properties of the FETI domain decomposition method," Computer Methods in Applied Mechanics and Engineering, vol. 115, no. 3–4, pp. 365–385, 1994.

17. C Guiffaut and K Mahdjoubi, "A parallel FDTD algorithm using the MPI library," IEEE Antennas and Propagation Magazine, vol. 43, no. 2, pp. 94–103, 2001.

18. H Ling, RC Chou, and SW Lee, "Shooting and bouncing rays: calculating the RCS of an arbitrarily shaped cavity," IEEE Transactions on Antennas and Propagation, vol. 37, no. 2, pp. 194–205, 1989.

19. PY Ufimtsev, "Improved physical theory of diffraction: removal of the grazing singularity," IEEE Transactions on Antennas and Propagation, vol. 54, no. 10, pp. 2698–2702, 2006.

20. RG Kouyoumjian and PH Pathak, "A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface," Proceedings of the IEEE, vol. 62, no. 11, pp. 1448–1461, 1974.

21. M Abadi, A Agarwal, P Barham, E Brevdo, Z Chen, C Citro et al., TensorFlow: large-scale machine learning on heterogeneous distributed systems, 2016. [Online]. Available: https://arxiv.org/abs/1603.04467

22. A Paszke, S Gross, F Massa, A Lerer, J Bradbury, G Chanan et al., "PyTorch: an imperative style, high-performance deep learning library," In: Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS); Vancouver, Canada. 2019, pp 8024–8035.

23. R Al-Rfou, G Alain, A Almahairi, C Angermueller, D Bahdanau, N Ballas et al., Theano: a python framework for fast computation of mathematical expressions, 2016. [Online]. Available: https://arxiv.org/abs/1605.02688

24. F Chollet, Keras: the python deep learning library, 2018. [Online]. Available: https://keras.io

25. Y Jia, E Shelhamer, J Donahue, S Karayev, J Long, RB Girshick, S Guadarrama, and TJ Darrell, "Caffe: convolutional architecture for fast feature embedding," In: Proceedings of the 22nd ACM International Conference on Multimedia; Orlando, FL. 2014, pp 675–678.

26. Y LeCun, L Bottou, Y Bengio, and P Haffner, "Gradient-based learning applied to document recognition," Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998.

27. K Simonyan and A Zisserman, "Very deep convolutional networks for large-scale image recognition," In: Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015); San Diego, CA. 2015.

28. P Isola, JY Zhu, T Zhou, and AA Efros, "Image-to-image translation with conditional adversarial networks," In: Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); Honolulu, HI. 2017, pp 5967–5976.

29. IJ Goodfellow, J Pouget-Abadie, M Mirza, B Xu, D Warde-Farley, S Ozair, A Courville, and Y Bengio, "Generative adversarial nets," In: Proceedings of the 27th International Conference on Neural Information Processing Systems; Montreal, Canada. 2014, pp 2672–2680.

30. JY Zhu, T Park, P Isola, and AA Efros, "Unpaired image-to-image translation using cycle-consistent adversarial networks," In: Proceedings of 2017 IEEE International Conference on Computer Vision (ICCV); Venice, Italy. 2017, pp 2242–2251.

31. M Ma, J Chen, W Liu, and W Yang, "Ship classification and detection based on CNN using GF-3 SAR images," Remote Sensing, vol. 10, no. 12, article no. 2043, 2018. https://doi.org/10.3390/rs10122043

32. S Bao, J Meng, L Sun, and Y Liu, "Detection of ocean internal waves based on Faster R-CNN in SAR images," Journal of Oceanology and Limnology, vol. 38, no. 1, pp. 55–63, 2020.

33. YL Chang, A Anagaw, L Chang, YC Wang, CY Hsiao, and WH Lee, "Ship detection based on YOLOv2 for SAR imagery," Remote Sensing, vol. 11, no. 7, article no. 786, 2019. https://doi.org/10.3390/rs11070786

34. A Krizhevsky, I Sutskever, and GE Hinton, "ImageNet classification with deep convolutional neural networks," Advances in Neural Information Processing Systems, vol. 25, pp. 1097–1105, 2012.

35. JR Diemunsch and J Wissinger, "Moving and stationary target acquisition and recognition (MSTAR) model-based automatic target recognition: search technology for a robust ATR," In: Proceedings of SPIE vol. 3370: Algorithms for Synthetic Aperture Radar Imagery V; Bellingham, WA, International Society for Optics and Photonics. 1998, pp 481–491.

36. DP Kingma and JL Ba, "Adam: a method for stochastic optimization," In: Proceedings of the 3rd International Conference on Learning Representations (ICLR); San Diego, CA. 2015.

Biography

Seung Mo Seo received a B.S. degree from Hong-Ik University, in 1998 and M.S. and Ph.D. degrees from The Ohio State University in 2001 and 2006, respectively, all in electrical engineering. From 1999 to 2006, he was a graduate research associate with the ElectroScience Laboratory (ESL), Department of Electrical and Computer Engineering, The Ohio State University, Columbus, where he focused on the development of fast integral equation methods. From 2007 to 2010, he was a senior engineer at the Digital Media and Communication (DMC) R&D Center, Samsung Electronics, where he developed an RF circuit and antenna design and simulation. From 2011 to the present, he has been a principal researcher at the Agency for Defense Development. From 2011 to 2016, he developed an anti-jamming satellite navigation system. His current research interest is synthetic aperture radar (SAR) and automatic target recognition (ATR). He is currently an IEEE senior member.

Biography

Yeoreum Choi received B.S. and M.S. degrees from the Department of Electrical Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, South Korea, in 2015 and 2017, respectively. He is currently a researcher at the Agency for Defense Development (ADD), Daejeon, South Korea. His research interests include deep learning with synthetic aperture radar (SAR) imagery.

Biography

Ho Lim received a B.S. in electronics engineering from Soongsil University, Seoul, Korea in 2006 and a Ph.D. from the Dept. of Electrical Engineering at KAIST, Daejeon, Korea in 2011. Since 2011, he has been working at the Agency for Defense Development as a senior research engineer. His research interests include SAR-ATD and ATR.

Biography

Dae-Young Chae received a B.S. in electronics engineering from Sungkyunkwan University, Suwon, Korea in 2006 and an M.S. in electrical and electronics engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea in 2008. Since 2008, he has been working at the Agency for Defense Development as a senior research engineer. His research interests include RCS analysis and SAR-ATR.