Substrate Integrated Waveguide Quasi-Elliptic Filter with Arbitrary Termination Impedances

Phanam Pech; Phirun Kim; Girdhari Chaudhary; Yongchae Jeong

doi:10.26866/jees.2022.4.r.111

J. Electromagn. Eng. Sci > Volume 22(4); 2022 > Article

Pech, Kim, Chaudhary, and Jeong: Substrate Integrated Waveguide Quasi-Elliptic Filter with Arbitrary Termination Impedances

Regular Paper

Journal of Electromagnetic Engineering and Science 2022;22(4):472-478.

Published online: July 31, 2022

DOI: https://doi.org/10.26866/jees.2022.4.r.111

Substrate Integrated Waveguide Quasi-Elliptic Filter with Arbitrary Termination Impedances

Phanam Pech¹, Phirun Kim^2,³, Girdhari Chaudhary^1,⁴, Yongchae Jeong^1,^*

¹Division of Electronic and Information Engineering, Jeonbuk National University, Jeonju, Korea

²Department of Frequency Spectrum Management, Ministry of Posts and Telecommunication of Cambodia, Phnom Penh, Cambodia

³Institute of Digital Research and Innovation, Cambodia Academy of Digital Technology, Phnom Penh, Cambodia

⁴BK21-FOUR JIANT-IT Human Resource Development Center, Jeonbuk National University, Jeonju, Korea

^*Corresponding Author: Yongchae Jeong (e-mail: ycjeong@jbnu.ac.kr)

Received October 14, 2021 Revised March 16, 2022 Accepted May 4, 2022

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

This paper presents a quasi-elliptic filter (QEF) with arbitrary termination impedances (ATI). The proposed QEF is designed by adding cross-coupling between the first and last resonators of an ATI bandpass filter (BPF) with the Chebyshev response. The proposed QEFs with ATI can be designed in even-order resonators and the location of the pair transmission zeros (TZs) is controllable. To prove the validity of the proposed design, the fourth-order QEFs with ATI were implemented on a single-layer substrate-integrated waveguide (SIW) cavity at a center frequency (f₀) of 10 GHz with the pair TZs at 10 ± 1.4 GHz. These SIW QEFs with ATI improve frequency selectivity and effectively suppress the out-of-band signal with high power handling. The measured maximum insertion loss (|S₂₁|) and minimum return loss (|S₁₁|) of the SIW QEF with unequal real-to-real ATI are 0.93 dB and 17.4 dB, respectively, in the passband. Similarly, the maximum |S₂₁| and minimum |S₁₁| of the SIW QEF with complex-to-real ATI are 1.2 dB and 18 dB, respectively.

Keywords: Arbitrary Termination Impedance, Quasi-Elliptic Filter, Substrate-Integrated Waveguide

I. Introduction

The arbitrary termination impedance (ATI) bandpass filter (BPF) plays an important role in modern communication systems. Fig. 1(a) shows the conventional radio frequency (RF) transmitter of a wireless system [1]. The ATI BPF can directly match the output impedance of the power transistor or the input impedance of the antenna to reduce the overall circuit size, insertion loss, cost, and complexity of the network as can be seen in Fig. 1(b). An unequal termination impedance power divider with a bandpass filtering response and a very low impedance transforming ratio (r) were proposed in [2]. The analysis was based on the characteristics of couple transmission lines (TLs).

Similarly, an arbitrary real-to-real termination impedance parallel-coupled TL BPF was presented in [3]. The BPF consisted of the multi-stage parallel-coupled TLs with different even- and odd-mode impedances. Recently, ATI BPF matching networks using λ/4 stepped impedance resonators were proposed in [4]. The structure consisted of open-ended parallel-coupled TLs and T-type TLs that were cascaded alternately. However, the aforementioned BPFs can be designed with Butterworth or Chebyshev responses which do not consider transmission zeros (TZs) for high out-of-band signal suppression. Moreover, those BPFs were analyzed and realized by using couple TLs, which may be difficult to fabricate when the center frequency (f₀) is increased to a higher operation band.

Substrate-integrated waveguide (SIW) filters with either real or complex termination impedance (CTI) are important circuits widely used in microwave applications, with a relatively high quality factor and low insertion loss (IL). As demand increases for a broader channel bandwidth and high out-of-band signal suppression, the demand for a quasi-elliptic filter (QEF) with finite TZs also grows. An equal termination impedance QEF with a broadband post-loaded electric coupling structure on a single-layer SIW was proposed in [5]. Further, an SIW QEF with controllable mixed electric and magnetic couplings using a three-layer printed circuit board (PCB) was proposed in [6]. Compact frequency-selective cascading SIW cavities with a quasi-elliptic response were also proposed based on the dual-mode filter theories found in [7]. Most recently, an SIW cavity QEF with slot coupling and non-adjacent cross-coupling was presented in [8]. In their designs, the slots etched on the top metal plane of the SIW cavity were used to produce electrical coupling, and cross-coupling was realized by the microstrip TL on the SIW cavity.

However, slots etched on the SIW cavity may increase the IL of the filter due to an increase in radiation loss. On the other hand, the SIW QEFs presented in [5–8] were designed with equal termination impedances of 50 Ω to 50 Ω. In [6–8], the circuits were implemented on a multi-layer PCB, which was a very difficult design process and had a high fabrication price. Recently, a synthesis approach for the design of a Chebyshev BPF with complex frequency variant loads was proposed in [9]. The proposed approach was based on the power wave renormalization theory and legitimate assumptions.

In this paper, a new SIW QEF with arbitrary real and/or complex termination impedances is introduced. The proposed SIW QEF can be designed easily by adding a parallel J-inverter between the first and last resonators, which is represented as cross-coupling. Furthermore, the location of the pair TZs is controllable for a good frequency-selective response. The proposed unequal real-to-real and complex-to-real termination impedance SIW QEFs are designed on a single-layer PCB that provides simpler design processes and a cheaper fabrication price.

II. Design Equations and Procedures

Fig. 2(a) shows an equivalent circuit with shun LC resonators and admittance inverters of the proposed ATI QEF, in which the ATIs are Z_S =R_S ± jX_S and Z_L = R_L ± jX_L. Fig. 2(b) presents the modified equivalent circuit of Fig. 2(a), which is based on the conventional ATI BPF presented in [10]. This QEF can be designed for ATIs with even coupled resonators. As mentioned in [10], matching the reactive parts of the termination impedances requires detuning the first and last resonators. In terms of capacitive or inductive compensations, the detuning frequency of the CTI using series reactive components is more beneficial than the addition of shunt reactive components. For fourth-order QEF, the first (f_S₁) and last (f₄_L) resonance frequencies are detuned from the f₀ on the basis of termination impedances and can be defined as follows:

(1)

fS1,4L=f0 [1+(XS,LFBW2RS,Lg0,4g1,5)2+XS,LFBW2RS,Lg0,4g1,5],

where R_S_,_L and X_S_,_L are the real and imaginary components of the source and load impedances, respectively. FBW is the fractional bandwidth of the passband, while g_i (i = 0, 1, 4, 5) is the element value of the low-pass prototype. The intermediate resonators are not changed by the CTI. C_i =1/ω²L_i

The capacitance of the parallel resonator can be calculated with C_i =1/ω²L_i by choosing an arbitrary value for the inductor (L_i) of the shunt parallel resonator. The slope parameters of the first, intermediate, and last resonators can be calculated using the following equations:

(2)

b1=ωS1C1,bi=bi+1=ω0Ci,b4=ω4LC4,

where ω_S₁ and ω₄_L are the detuned angular frequencies (which can be found from Eq. (1)) and ω₀ is an angular center frequency.

Once the detuned frequencies and slope parameters have been determined, the J-inverters of the coupled-resonator can be defined as follows:

(3)

J01=FBWb1RSg0g1,Ji,i+1=FBWbibi+1gigi+1,J45=FBWb4RLg4g5,i=1,2,3,

The transfer function and design examples of the conventional QEF were presented in [11]. A similar approach can be used to determine the frequency location of the pair TZs:

(4)

Ωa=1FBW(ωTZ-Hω0-ω0ωTZ-H),

where Ω_a and ω_TZ–H are the frequency variable normalized to ω₀ and the angular frequency of TZ at the higher side, respectively.

The quasi-elliptic response can be achieved through the addition of a parallel J₁₄ between the first and fourth resonators. The pair TZs are located at the frequency f_TZ = f₀ ± a. Furthermore, J₁₄ is the function of Ω_a (or f_TZ–H) and can be determined through Eq. (5):

(5)

J14=J12J122-(Ωag2)2.

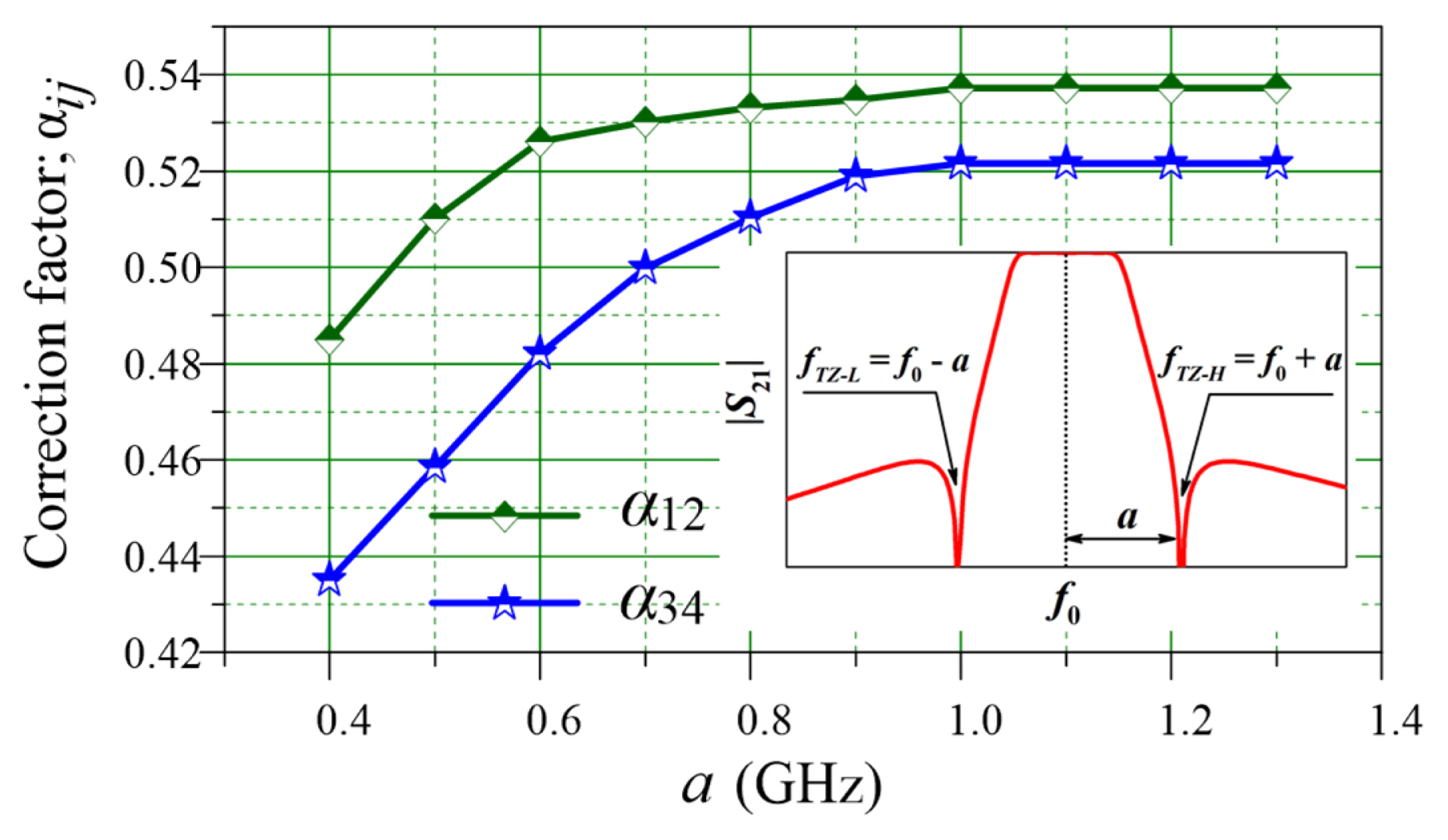
The filter will be mismatched once J₁₄ is added. To maintain the required return loss (RL) at the operating band, the values of J₁₂ and J₃₄ must be slightly modified. Fig. 3 presents the correction factor values used to calculate the new J12′ and J34′ based on the location of TZs. The correction factors can be obtained using computer synthesis according to the required RL. The new J-inverters can be determined using the following equations:

(6)

J12′=J12 (Ωa(α12+1)g1g2-1),J34′=J34 (Ωa(α34+1)g3g4-1),

where the correction factors are α₁₂ for J₁₂ and α₃₄ for J₃₄. These correction factors are critical to determining the location of TZs near the f₀. If the TZs are located slightly far from f₀ or a > 1, J₁₄ exerts only a small effect on the RL of the filter and results in very small cross-coupling. The external quality factors and coupling coefficients of the resonators are defined as follows [8]:

(7a)

QS1=b1RSJ012,Q4L=b4RLJ4,52,

(7b)

Ki,i+1=Ji,i+1bibi+1,K14=J14b1b4,

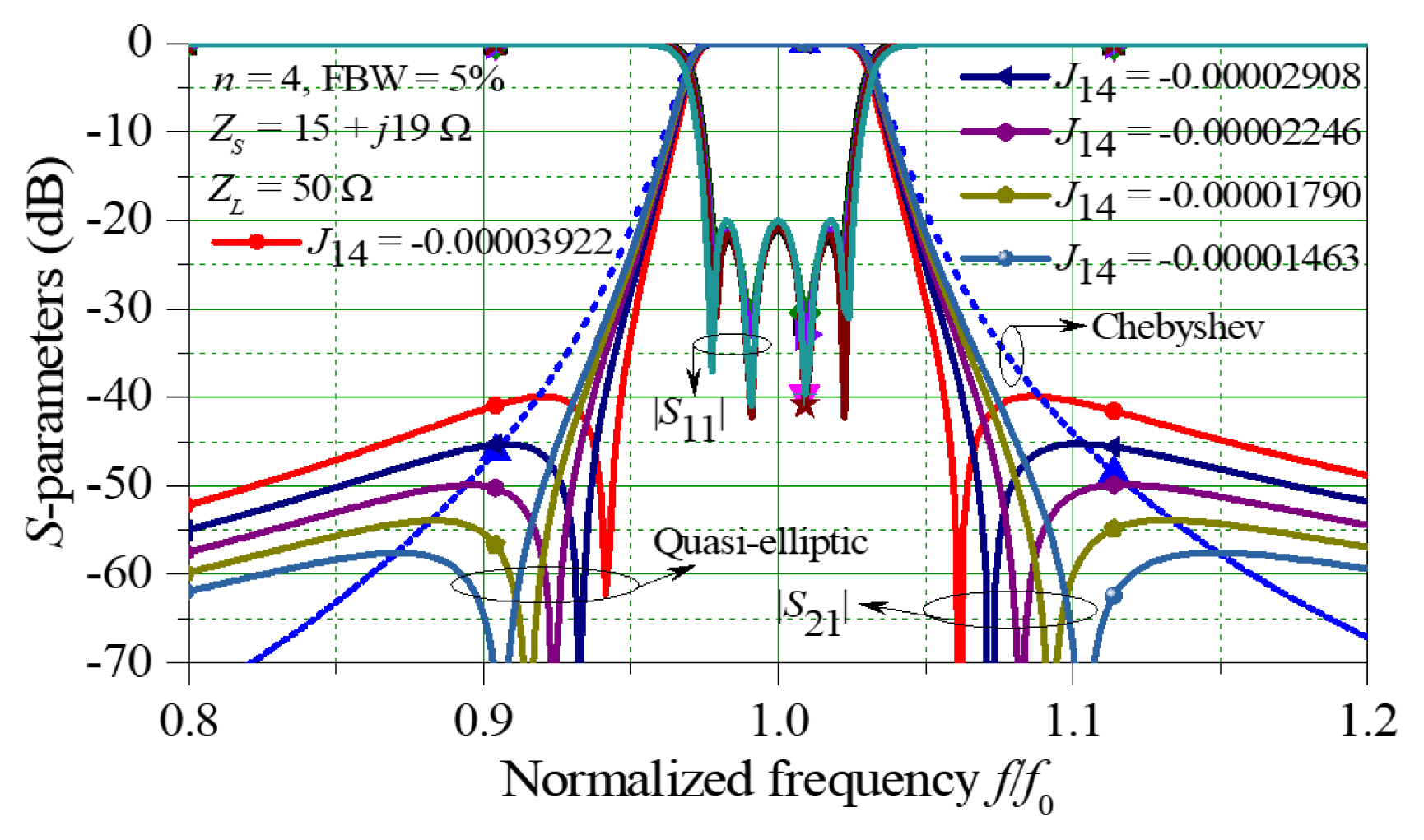
where Q_S₁ and Q₄_L are the external quality factors of the first and fourth resonators, respectively. Then, K_i_, _i+₁ is an inline coupling coefficient, while K₁₄ is cross-coupling coefficient of the resonators. To demonstrate the analysis, the QEFs are designed with the CTI and the different locations of TZs. The lossless elements of the J-inverter and the LC resonators are used in the simulation. The circuit model is simulated with the Advanced Design System (ADS) software. Fig. 4 provides the S-parameters of the QEFs (FBW = 5% and |S₁₁| = 20 dB), according to the location of the TZs. The QEFs were designed with source termination of Z_S = 15 + j19 Ω and the load termination impedance of Z_L = 50 Ω. The required RL can be obtained by using the proper correction factors.

III. Design of SIW QEF with CTI

The SIW QEFs with ATI are designed using positive and negative couplings with via-hole windows. The proposed SIW QEF was designed with f₀ of 10 GHz, FBW of 5 %, and |S₁₁| of 20 dB. The frequency locations of TZ are 8.6 GHz and 11.4 GHz (a = 1.4). For an unequal real-to-real case, the ATIs are Z_S = 20 Ω and Z_L = 50 Ω. Further, L₁= L₂ = L₃ = L₄ = 2 nH was selected, while C₁ = C₂ = C₃ = C₄ = 0.1266 pF is calculated from Eq. (2). Using Eq. (3)J-inverters can be determined as J₀₁ = 0.004616, J₁₂ = 0.000362, J₂₃ = 0.000278, J₃₄ = 0.000362, and J₄₅ = 0.00292. During the final step, J₁₄ = −0.000088 is calculated using Eq. (5).

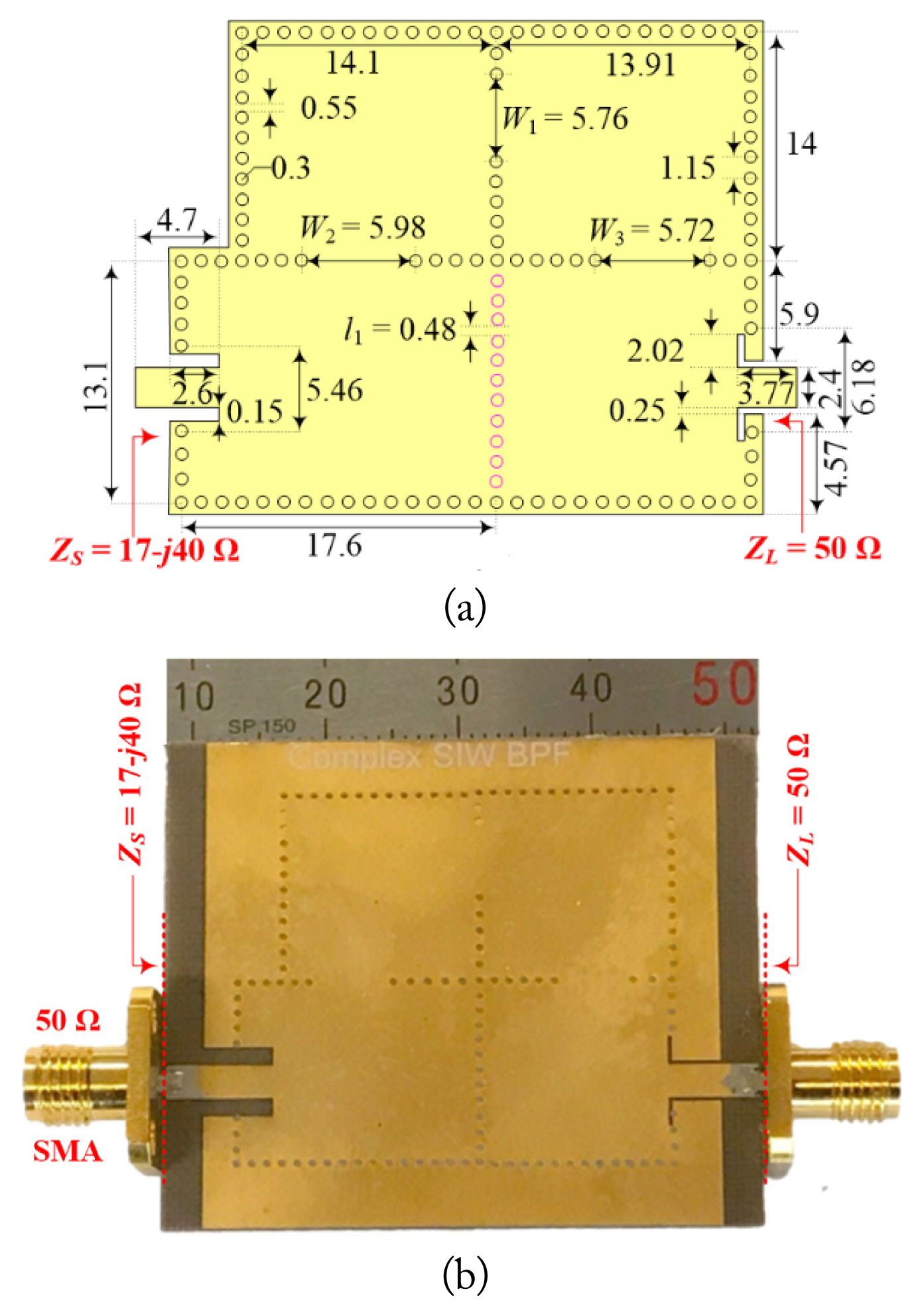
For a complex-to-real case, the ATIs are Z_S = 17 − j40 Ω and Z_L = 50 Ω. Further, f_S₁ is calculated from Eq. (1) and detuned to 10.65 GHz. Then, L₁= L₂ = L₃ = L₄ = 2 nH was selected, while C₁ = 0.1116 pF and C₂ = C₃ = C₄ = 0.1266 pF. Similarly, J₀₁ = 0.004852, J₁₂ = 0.000351, J₂₃ = 0.000278, J₃₄ = 0.000362, J₄₅ = 0.00292, and J₁₄ = −0.00000761 are calculated. Because a > 1, the modifications of J₁₂ and J₃₄ for maintaining |S₁₁| = 20 dB are not required.

In praxis, shunt LC resonators can be constructed in various forms, such as a TL resonator, waveguide resonator, or SIW resonator [12, 13]. The external quality factor of the source (Q_S) and the load (Q_L) can be extracted from the electromagnetic (EM) simulation. In addition, Q_S and Q_L can be calculated using Eq. (8).

(8)

QS_EM,L_EM=fS1,4LΔf±3dB,

where Δf_±₃_dB is a 3-dB bandwidth.

The coupling coefficients between resonators can also be extracted from the EM simulation using Eq. (9) for synchronously tuned coupled resonators.

(9)

K=±fH2-fL2fH2+fL2,

where f_H and f_L denote the higher and lower resonant frequencies, respectively. A quality factor of around 500 can be obtained from an eigen-mode simulation.

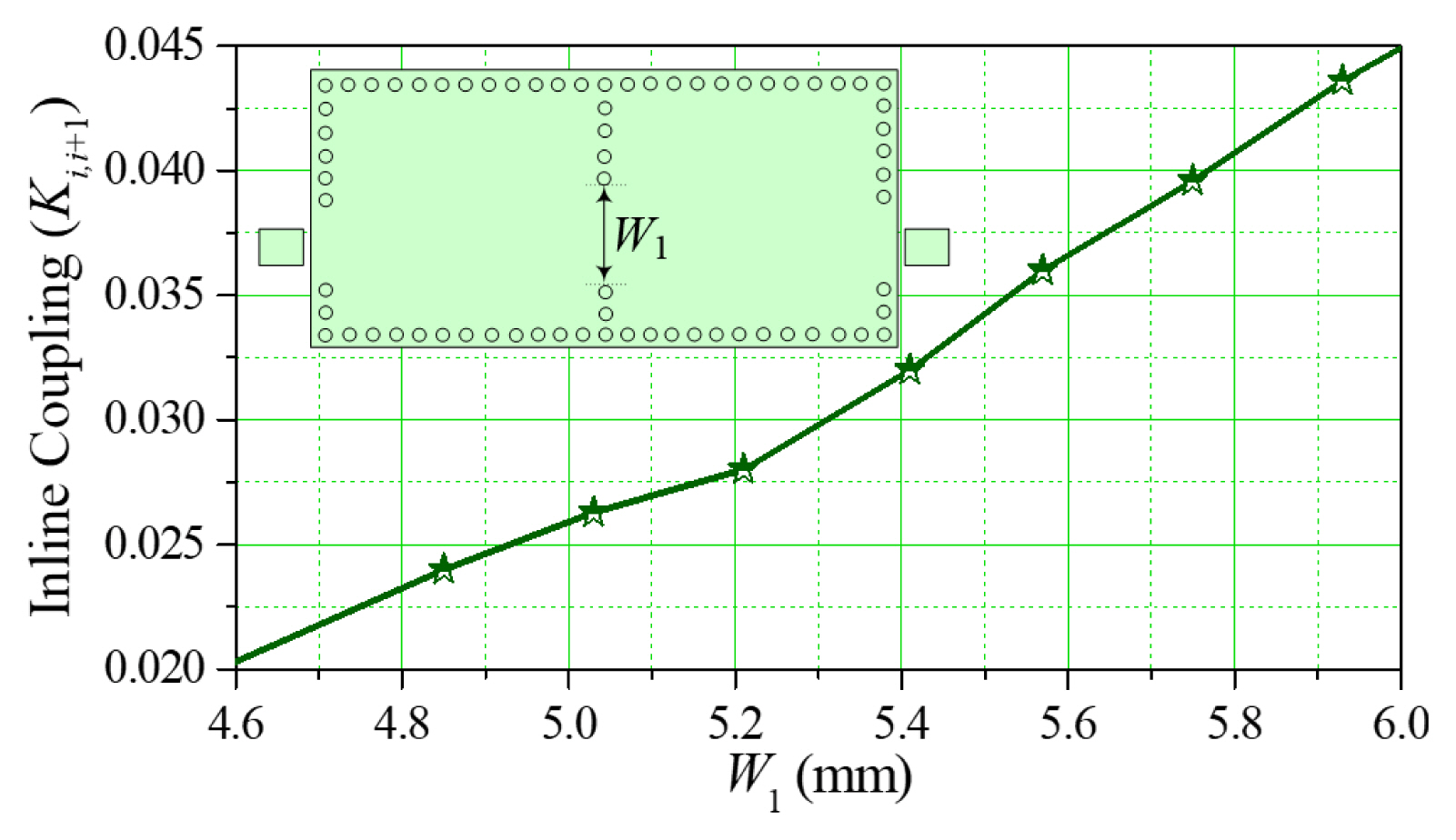
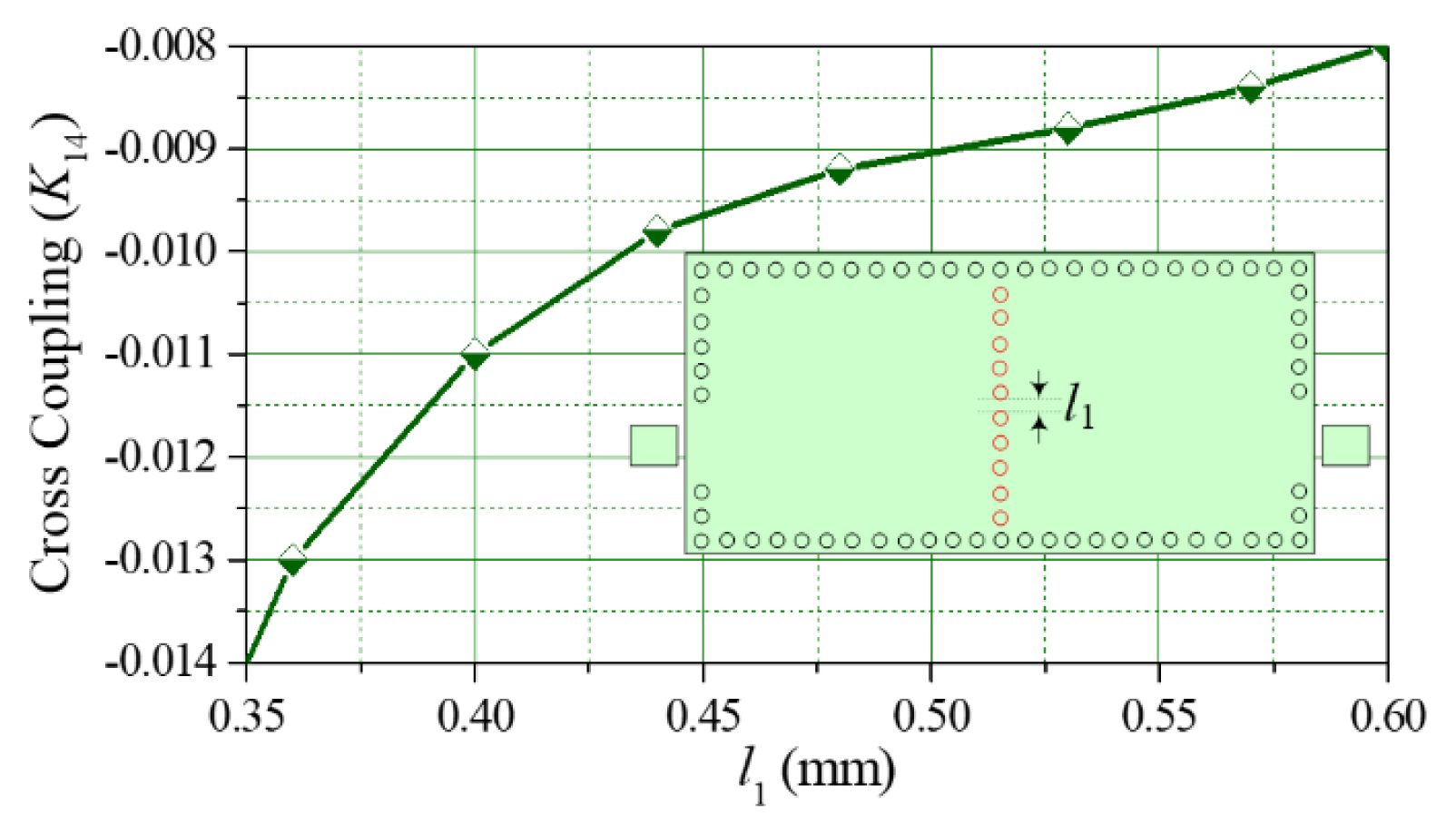
Fig. 5 illustrates the inline coupling coefficient (K_i_,_i₊₁) of two rectangular SIW cavities. The K_i_,_i₊₁ is increased as the width of the iris window (W₁) expands. Similarly, Fig. 6 shows the leakage or cross-coupling coefficient (K₁₄) according to the viahole wall spacing (l₁) between the first and fourth resonators. K₁₄ has been shown to increase rapidly as l₁ grows.

IV. Simulation and Measurement Results

The SIW QEFs with unequal real-to-real and complex-to-real ATIs were designed and implemented on RT/Duriod 5880 substrate with ɛ_r = 2.2 and h = 0.787 mm.

The layouts with dimensions of the proposed unequal real-to-real ATI SIW QEFs, as well as a photograph, are provided in Fig. 7. The measurement results are consistent with those obtained by the simulation. Fig. 8(a) depicts the measured matching impedance point of the proposed real-to-real ATI SIW QEF on a Smith chart. The measured real source termination impedance is well matched to that obtained by the EM simulation. Similarly, the S-parameters within frequency range of 2–18 GHz are likewise presented in Fig. 8(b); a measured 3 dB bandwidth range between 9.75 and 10.25 GHz (FBW = 5%) is obtained. The measured minimum |S₁₁| is 17.4 dB and maximum |S₂₁| is 0.93 dB in the passband. The spurious response is produced at approximately 14.5 GHz (1.45f₀). The stopband attenuation better than 35 dB at the lower side of the passband is between 2 GHz and 9 GHz and at the higher side of the passband is between 11 GHz and 14.3 GHz. Similarly, a minimum attenuation better than 18.5 dB is obtained between 14.4 GHz and 18 GHz.

The layouts with dimensions of the proposed complex-to-real ATI SIW QEFs, as well as a photograph, are provided in Fig. 9. Further, Fig. 10(a) depicts the measured matching impedance point of the proposed complex-to-real ATI SIW QEF on a Smith chart. The measured complex source termination impedance is well matched to that obtained by the EM simulation. The S-parameters within the frequency range of 2–18 GHz are likewise presented in Fig. 10(b); a measured 3 dB bandwidth range between 9.74 and 10.25 GHz (FBW = 5.1%) is obtained. The measured minimum |S₁₁| is 18 dB and maximum |S₂₁| is 1.2 dB in the passband. The spurious response is produced at approximately 14.5 GHz (1.45f₀). The stopband attenuation better than 40 dB occurs at the lower side of the passband between 2 GHz and 9 GHz and at the higher side of the passband, between 11 GHz and 14 GHz. Similarly, a minimum attenuation better than 16 dB is obtained between 14.1 GHz and 18 GHz.

The performances of the proposed SIW QEF with ATIs are compared with state-of-the-art BPFs and SIW QEFs in Table 1. The proposed SIW QEFs are designed on a single-layer PCB with unequal real-to-real and complex-to-real ATIs, which are inexpensive and uncomplicated to fabricate. In view of the conductor and dielectric losses, which are related to the operating frequency and FBW, the proposed SIW QEF provides a smaller IL in the passband than conventional SIW QEFs.

V. Conclusion

A new design for an SIW QEF with ATI is proposed and investigated in this paper. The proposed SIW QEFs provide high frequency selectivity and out-of-band signal suppression. The SIW QEF with ATI may be useful in, for example, the input and/or output matching networks of the power amplifier, which may reduce the insertion loss and complexity of the transmitter in the RF front end. In addition, the proposed SIW QEFs design method can be applied to a microwave circuit and system designs.

Acknowledgments

This work was supported by the National Research Foundation (NRF) of Korea Grant funded by the Korean Government (MSIT) (Grant No. 2020R1A2C2012057) and in part by the Basic Science Research Program through the NRF of Korea, funded by the Ministry of Education (Grant No. 2019R1A6A1A09031717).

Fig. 1

RF transmitters of a wireless system with (a) conventional matching networks and BPF and (b) ATI BPF

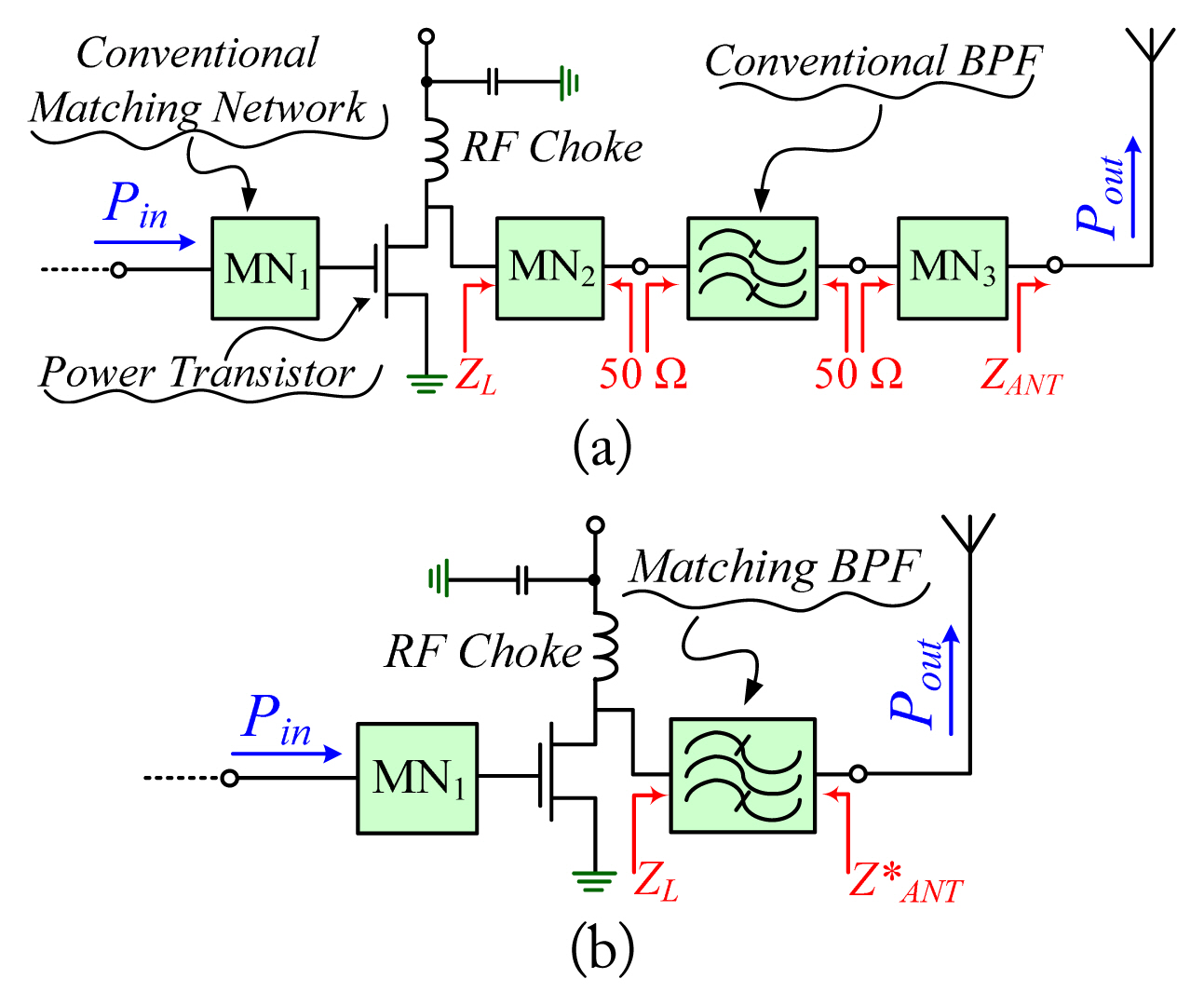
Fig. 2

(a) ATI QEF with shunt inductor-capacitor (LC) resonators and admittance inverters and (b) the modified equivalent circuit of (a).

Fig. 3

Correction factors (α_ij) according to the location of TZs.

Fig. 4

S-parameters of the CTI filter with Chebyshev and quasi-elliptic responses.

Fig. 5

Coupling coefficient according to the width of the iris window (W₁).

Fig. 6

Magnetic coupling coefficient of two rectangular SIW cavities according to the gap (l₁).

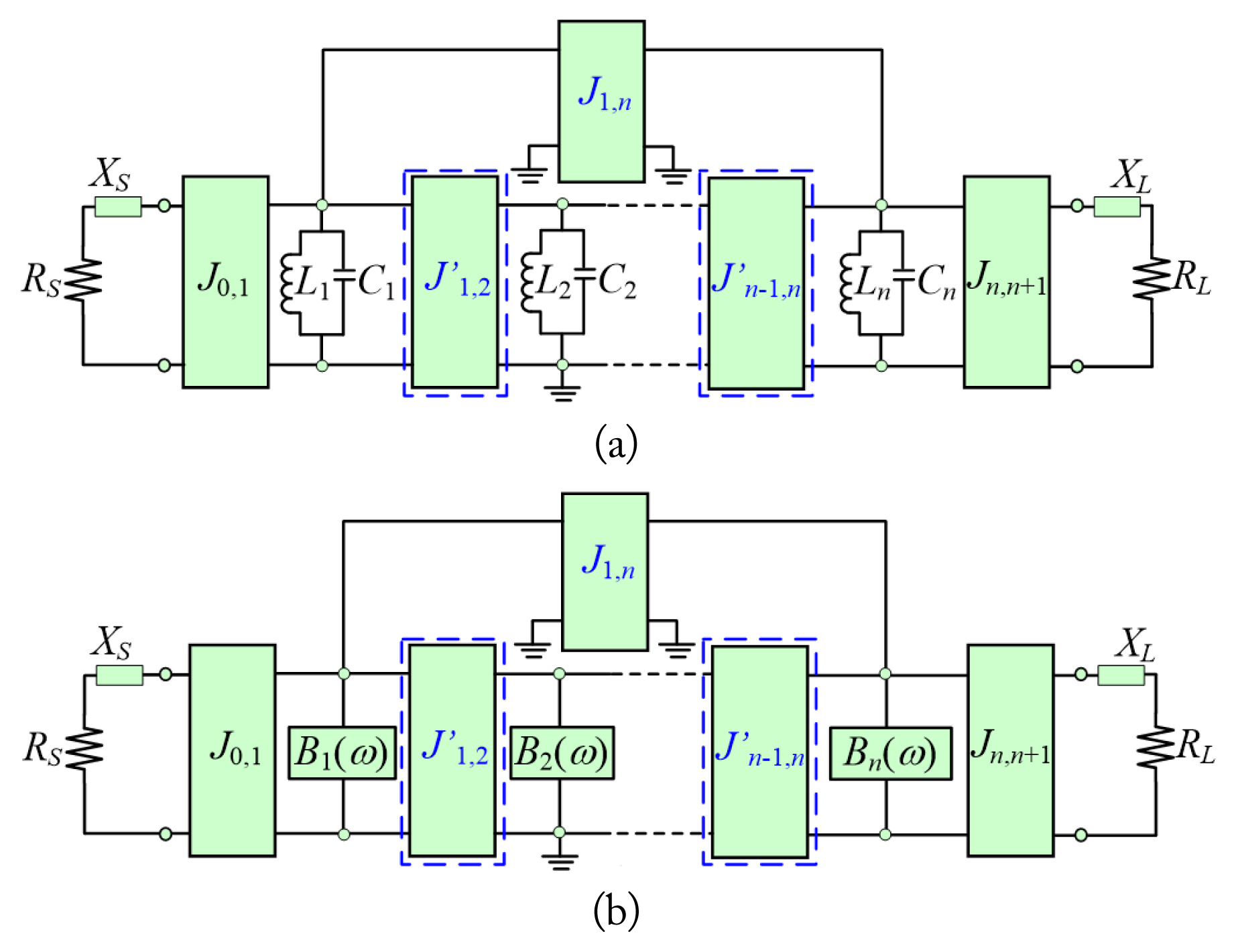
Fig. 7

Proposed unequal real-to-real SIW QEFs: (a) layout with dimension and (b) fabricated circuit.

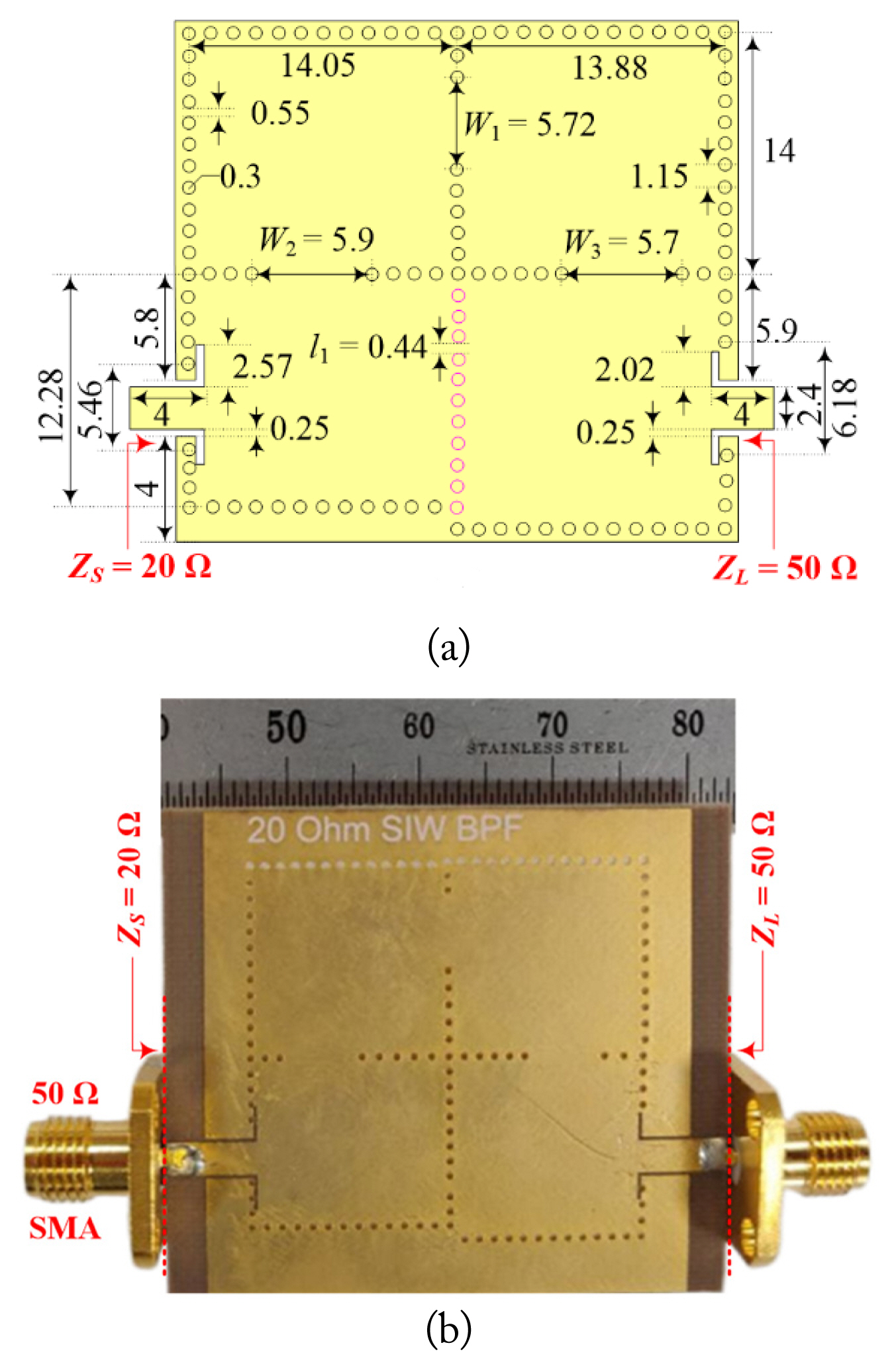
Fig. 8

Comparison between the EM simulation and measurement results of the unequal real-to-real ATI SIW QEF: (a) matching impedance point on the Smith-chart and (b) magnitude of S-parameters.

Fig. 9

Proposed complex-to-real SIW QEFs: (a) layout with dimension and (b) fabricated circuit.

Fig. 10

Comparison between the EM simulation and measurement results of the complex-to-real ATI SIW QEF: (a) matching impedance point on the Smith-chart and (b) S-parameters.

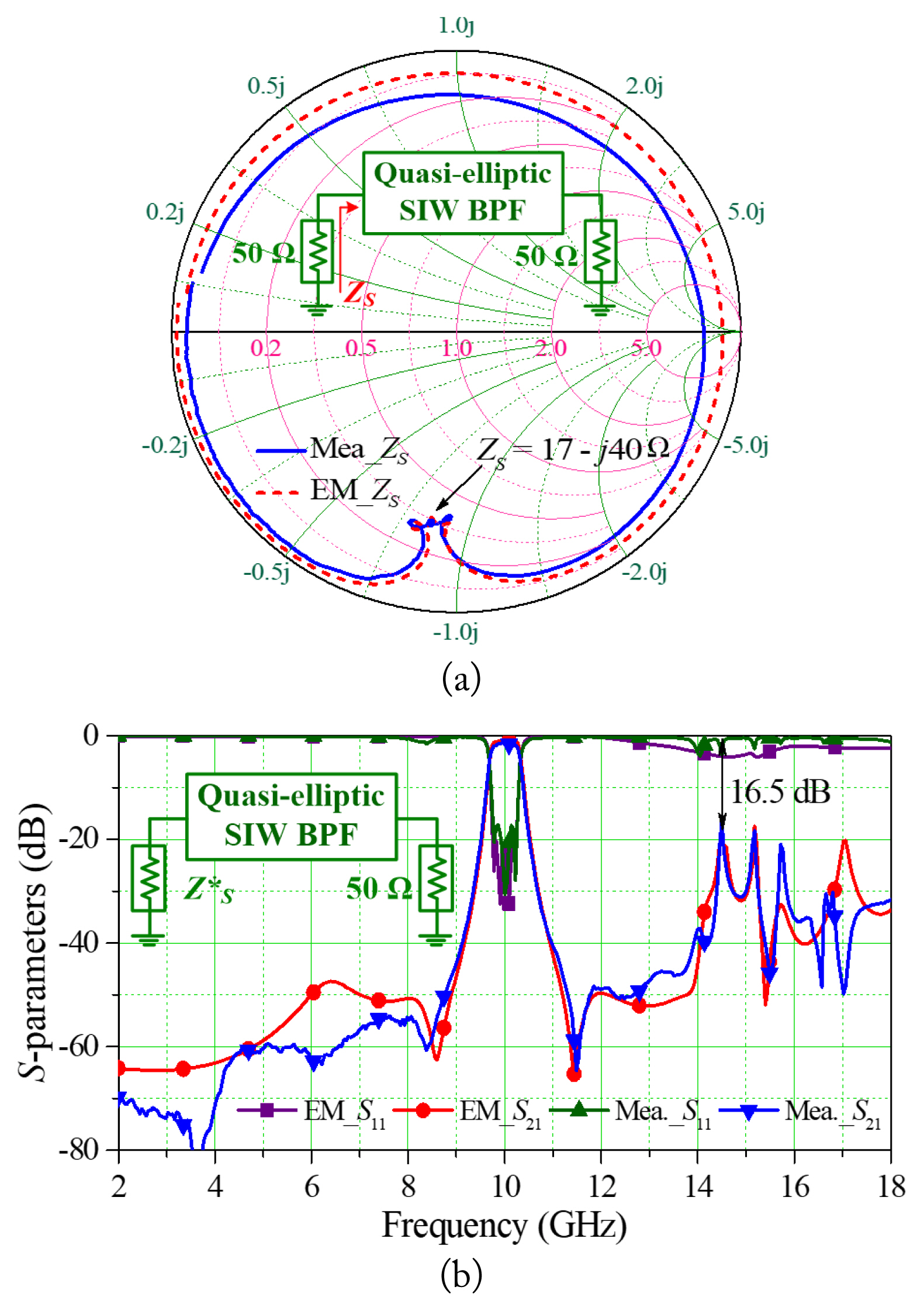
Table 1

Comparison of performances with previous works

Study	f₀ (GHz)	FBW (%)	n	Circuit	\|S₂₁\| (dB)	PCB lay.	TZs	Attenuation (@ 0.9f₀ and 1.1f₀)	Term. imped. (Ω)
Kim et al. [3]	2.6	5	2	Couple TL	0.8	1	No	≈11, ≈ 12 dB	50-to-300
Kim et al. [3]	2.6	5	3	Couple TL	1.5	1	No	≈26, ≈ 30 dB	20-to-50
Kim and Jeong [4]	2.6	5.3	2	Couple TL	0.89	1	No	≈15, ≈ 17 dB	30 + j10-to-50
Kim and Jeong [4]	2.6	5	3	Couple TL	1.3	1	No	≈28, ≈ 28 dB	50-to-100 – j100
You et al. [5]	5.5	12	4	SIW	1.68	1	2	≈27, ≈ 33 dB	50-to-50
You et al. [5]	5.8	3	4	SIW	6.35	1	2	≈42, ≈ 43 dB	50-to-50
Luo et al. [7]	30	1.67	4	SIW	2.5	3	2	≈29, ≈ 18 dB	50-to-50
Wong et al. [8]	3.7	16	4	SIW	1.1	2	2	≈25, ≈ 15 dB	50-to-50
This work	10	5	4	SIW	0.93	1	2	≈50, ≈ 40 dB	20-to-50
This work	10	5	4	SIW	1.2	1	2	≈44, ≈ 41 dB	17 – j40-to-50

References

1. B. Razavi, RF Microelectronics. 2nd ed. New Delhi, India: Pearson, 2012. p.157–250.

2. P. Kim, G. Chaudhary and Y. Jeong, "Analysis and design of an unequal termination impedance power divider with bandpass filtering response," Electronics Letters, vol. 53, no. 18, pp. 1260–1262, 2017.

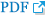
3. P. Kim, G. Chaudhary and Y. Jeong, "Unequal termination impedance parallel-coupled lines band-pass filter with arbitrary image impedance," Journal of Electromagnetic Waves and Applications, vol. 32, no. 8, pp. 984–996, 2018.

4. P. Kim and Y. Jeong, "A new synthesis and design approach of a complex termination impedance bandpass filter," IEEE Transactions on Microwave Theory and Techniques, vol. 67, no. 6, pp. 2346–2354, 2019.

5. C. J. You, Z. N. Chen, X. W. Zhu and K. Gong, "Single-layered SIW post-loaded electric coupling-enhanced structure and its filter applications," IEEE Transactions on Microwave Theory and Techniques, vol. 61, no. 1, pp. 125–130, 2013.

6. K. Gong, W. Hong, Y. Zhang, P. Chen and C. J. You, "Substrate integrated waveguide quasi-elliptic filters with controllable electric and magnetic mixed coupling," IEEE Transactions on Microwave Theory and Techniques, vol. 60, no. 10, pp. 3071–3078, 2012.

7. G. Q. Luo, W. Hong, Q. H. Lai, K. Wu and L. L. Sun, "Design and experimental verification of compact frequency-selective surface with quasi-elliptic bandpass response," IEEE Transactions on Microwave Theory and Techniques, vol. 55, no. 12, pp. 2481–2487, 2007.

8. S. W. Wong, R. S. Chen, J. Y. Lin, L. Zhu and Q. X. Chu, "Substrate integrated waveguide quasi-elliptic filter using slot-coupled and microstrip-line cross-coupled structures," IEEE Transactions on Components, Packaging and Manufacturing Technology, vol. 6, no. 12, pp. 1881–1888, 2016.

9. H. Meng, P. Zhao, K. L. Wu and G. Macchiarella, "Direct synthesis of complex loaded Chebyshev filters in a complex filtering network," IEEE Transactions on Microwave Theory and Techniques, vol. 64, no. 12, pp. 4455–4462, 2016.

10. P. Pech, P. Kim and Y. Jeong, "Microwave amplifier with substrate integrated waveguide bandpass filter matching network," IEEE Microwave and Wireless Components Letters, vol. 31, no. 4, pp. 401–404, 2021.

11. G. L. Matthaei, L. Yong and E. M. T. Jones, Microwave Filter, Impedance-Matching Networks, and Coupling Structures. New York, NY: McGraw-Hill, 1964.

12. J. Jeong, P. Kim, P. Pech, Y. Jeong and S. Lee, "Substrate-integrated waveguide impedance matching network with bandpass filtering," In: Proceedings of 2019 IEEE Radio and Wireless Symposium (RWS); Orlando, FL. 2019; pp 1–3.

13. J. S. Hong, Microstrip Filter for RF/Microwave Applications. 2nd ed. New York, NY: Wiley, 2011.

Biography

Phanam Pech received his B.Tech. degree in electronics engineering from the National Polytechnic Institute of Cambodia, Phnom Penh, Cambodia, in 2016, and his ME degree in electronics engineering from Jeonbuk National University, Jeonju, Republic of Korea, in 2019, where he is currently pursuing his PhD. From November 2016 to August 2017, he worked as a contract lecturer at the Faculty of Electronic Engineering, National Polytechnic Institute of Cambodia. His research interests include the design of microwave circuits, such as power amplifiers, low noise amplifiers, planar passive filters, matching networks with filtering response, power dividers, and RF front end transmitting systems.

Biography

Phirun Kim received his B.E. degree in electronics engineering from the National Polytechnic Institute of Cambodia, Phnom Penh, Cambodia, in 2010, and his M.E. degree and Ph.D. in electronics engineering from Jeonbuk National University, Jeonju, Republic of Korea, in 2013 and 2017, respectively. From February 2017 to August 2020, he worked as a contract professor at the HOPE-IT Human Resource Development Center of BK21 PLUS, Division of Electronic Engineering, Jeonbuk National University. He is currently working as a researcher at the Ministry of Posts and Telecommunication of Cambodia and the Institute of Digital Research and Innovation of the Cambodia Academy of Digital Technology. He has authored and co-authored over 60 papers for international journals and conference proceedings. His research interests include planar passive filters, power dividers, impedance transformers, baluns, and high-efficiency power amplifiers.

Biography

Girdhari Chaudhary received his B.E. and M.Tech. degrees in electronics and communication engineering from Nepal Engineering College, Kathmandu, Nepal and MNIT, Jaipur, India, in 2004 and 2007, respectively. He finished his Ph.D. in electronics engineering from Jeonbuk National University, Republic of Korea in 2013. He is currently working as an assistant research professor at the Division of Electronics Engineering, BK21-FOUR JIANT-IT Human Resource Development Center, Jeonbuk National University, Korea. Previously, he worked as a principal investigator on an independent project as part of the Basic Science Research Program administrated by the NRF and funded by the Ministry of Education. He is a recipient of the BK21 PLUS Research Excellence Award 2015 from the Korean Ministry of Education. He has also received a Korean Research Fellowship (KRF) through the NRF funded by the Ministry of Science and ICT. His research interests include multi-band tunable passive circuits, in-band full duplex systems, high efficiency power amplifiers, and the applications of negative group delay circuits.

Biography

Yongchae Jeong received his B.S.E.E. and M.S.E.E., and Ph.D. degrees in electronics engineering from Sogang University, Seoul, Republic of Korea in 1989, 1991, and 1996, respectively. Between 1991 and 1998, he worked as a senior engineer at Samsung Electronics in Seoul, Republic of Korea. In 1998, he joined the Division of Electronics Engineering, Jeonbuk National University, Jeonju, Republic of Korea. Between July 2006 and December 2007, he worked as visiting professor at the Georgia Institute of Technology. He is a professor as well as a member of the IT Convergence Research Center. At Jeonbuk National University, he also served as the director of the HOPE-IT Human Resource Development Center of BK21 PLUS. He is Jeonbuk National University’s vice-president of planning and continues to teach and research passive and active microwave circuits, mobile and satellite base-station RF systems, periodic defected transmission lines, negative group delay circuits and their applications, the in-band full duplex radio, and the RFIC design. Prof. Jeong is a senior member of IEEE and a member of KIEES. He has authored and co-authored over 260 papers for international journals and conference proceedings.