The Gain Estimation of a Fabry-Perot Cavity (FPC) Antenna with a Finite Dimension
Article information
Abstract
In this paper, we have presented an equation for estimating the gain of a Fabry-Perot cavity (FPC) antenna with a finite dimension. When an FPC antenna has an infinite dimension and its height is half of a wavelength, the maximum gain of that FPC antenna can be obtained theoretically. If the FPC antenna does not have a dimension sufficient for multiple reflections between a partially reflective surface (PRS) and the ground, its gain must be less than that of an FPC antenna that has an infinite dimension. In addition, the gain of an FPC antenna increases as the dimension of a PRS increases and becomes saturated from a specific dimension. The specific dimension where the gain starts to saturate also gets larger as the reflection magnitude of the PRS becomes closer to one. Thus, it would be convenient to have a gain equation when considering the dimension of an FPC antenna in order to estimate the exact gain of the FPC antenna with a specific dimension. A gain versus the dimension of the FPC antenna for various reflection magnitudes of PRS has been simulated, and the modified gain equation is produced through the curve fitting of the full-wave simulation results. The resulting empirical gain equation of an FPC antenna whose PRS dimension is larger than 1.5λ0 has been obtained.
I. Introduction
Many different types of antennas can be used to obtain high gain performances, such as a reflector antenna or an array of antennas [1, 2]. In the case of a reflector antenna, the required optimum focus length makes these antennas bulky. In addition, if the number of antennas in an array increases, the array will have a complex feed network with a loss that cannot be ignored. For decades, the Fabry-Perot cavity (FPC) antenna has been researched to overcome these drawbacks and obtain a high gain. When the phases of transmitted powers by multiple reflections between a partially reflective surface (PRS) and the ground are in-phase, the FPC antenna, which was introduced by Trentini [3] in the 1950s, can obtain a maximum gain.
Many related papers have been published to improve the performance using methods such as a broad bandwidth and a low profile [4–6]. Most research is based on ideal cases, which means that the dimension of an FPC antenna is assumed to be infinite. However, an FPC antenna has a finite dimension in many practical applications.
In this paper, an FPC antenna with a finite dimension has been studied to calculate its gain. If the dimension of the FPC antenna is infinite, its gain is proportional to the reflection magnitude of a PRS. However, the gain of an FPC antenna with a finite dimension depends on its dimension as well as the reflection magnitude of a PRS, so the gain equation of a finite-sized FPC antenna should include both parameters.
II. Operation Principle of an FPC Antenna
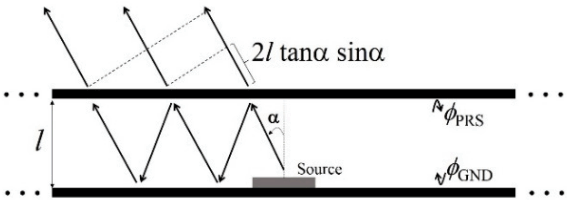
Fig. 1 shows multiple reflections between a PRS and the ground with the source. The planar patch antenna is employed as the source. When the source antenna is located inside a cavity (as shown in Fig. 1) and the total efficiency of the antenna equals 100%, the gain of the FPC antenna is given by the following equation [3]:
where ΓPRS is the reflection magnitude of the PRS, φGND is the reflection phase of the ground plane, φPRS is the reflection phase of the PRS, l is the distance between the PRS and the ground, and f2 is the radiation pattern of the source. If the FPC antenna has obtained its maximum gain, the denominator in the modification must be the minimum value, and
III. Gain Equation of an FPC Antenna with a Finite Dimension
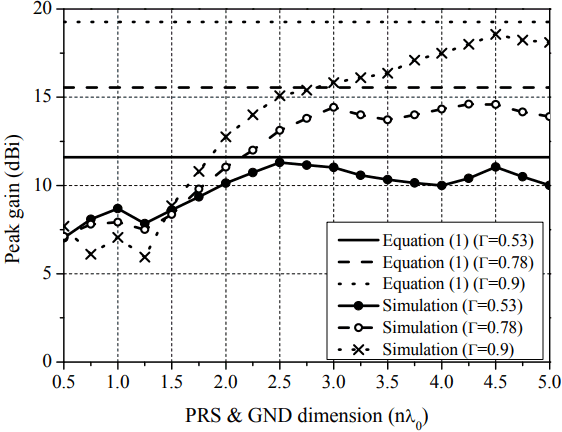
If the dimension of the ground and the PRS is infinite, the gain of the FPC antenna only depends on the reflection magnitude of the PRS from Eq. (1). However, when the FPC antenna has a finite dimension, the equation should be modified to include the effects of the finite PRS dimension. Fig. 2 shows the structure of the FPC antenna with a finite dimension (w × w). The source antenna operating at 5 GHz is located on the center of the ground. The utilized substrate for the antenna has the relative permittivity of 10.2 and a thickness of 1.6 mm. Three cases with different PRS reflection magnitudes of 0.53, 0.78, and 0.9 have been simulated. In addition, to obtain the PRS’s reflection magnitudes, we have used substrates, which have a fixed thickness at 3.2 mm and permittivity values of 6.15, 10.2, and 20. In addition, the height of a PRS from the ground (l) can be calculated using Eq. (2). Fig. 3 shows the simulated peak gains and Eq. (1) versus the dimension of an FPC antenna using various reflection magnitudes of a PRS. The simulated results were obtained using the ANSYS HFSS simulator (ANSYS Inc., Canonsburg, PA, USA). As shown in Fig. 3, the peak gain calculated by Eq. (1) with an infinite dimension is independent of the dimension of a PRS and is different from the full-wave simulated peak gain. All gain values versus the dimension of the FPC antenna go up and down because of the edge diffraction effect due to a finite ground condition. The full-wave simulated peak gain of an FPC antenna also increases and becomes saturated due to a specific dimension. The specific dimension where the gain starts to saturate increases as the reflection magnitude of a PRS becomes closer to one. To guarantee the number of multiple reflections to reach the maximum gain, the sufficient dimension of a PRS is required. Otherwise, the reflected wave would leak from the FPC antenna, resulting in a lower gain. Even though the reflection magnitude of the PRS is close to one in the case of a finite dimension with about 1.5λ0 or less, the gain of the FPC antenna cannot reach its maximum value (as shown in Fig. 3). The reason for this is because the larger the reflection magnitude of a PRS is, the bigger the dimension of a maximum gain should be. It has also been noted that, when the dimension of the PRS and the ground is less than 1.5λ0, the edge diffraction is dominant compared to the effect of multiple reflections. Eq. (1), which is proportional to the reflection magnitude of a PRS, is reasonable and valid in the case of a finite dimension with about 1.5λ0 or more. Therefore, by using the curve fitting from the simulated results where the dimension is 1.5λ0 or more, the equation for the peak gain required in order to include the dimension of an FPC antenna can be obtained with Eqs. (3) and (4).
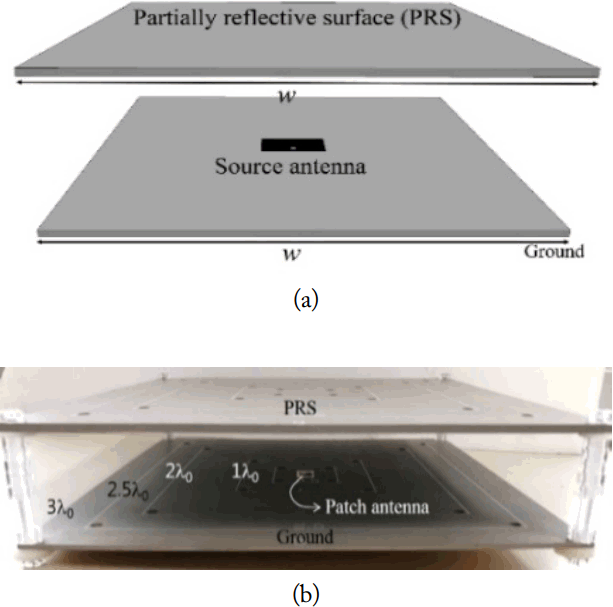
(a) Structure of an FPC antenna with a finite dimension and (b) a photograph of a fabricated FPC antenna.
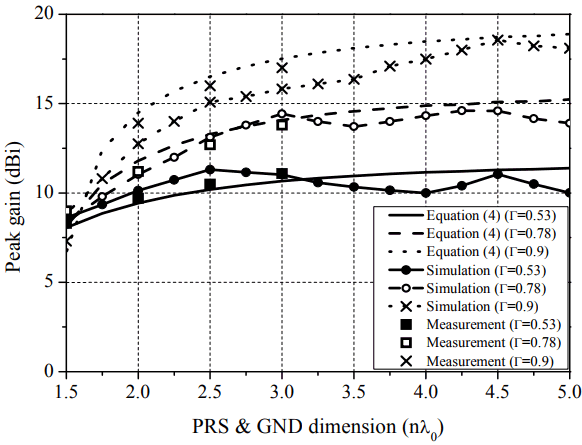
where ΓPRS is the reflection magnitude of the PRS and n (=w/λ0) is the normalized dimension of an FPC antenna by the free space wavelength. Fig. 4 presents the peak gains with Eq. (4), the simulation, and the measurement versus the dimension of an FPC antenna for various reflection magnitudes of a PRS. The peak gain was measured in the anechoic chamber system to confirm the accuracy of the proposed gain equation. The anechoic chamber is composed of a shield enclosure (4 m × 2.5 m × 2.5 m), a pyramidal absorber, a network analyzer, a positioner, a turn table, and a dual polarized transmitting antenna. The peak gains calculated from Eq. (4) are in good agreement with the simulated and measured results. Since Eq. (4) is a function of both a dimension and a reflection magnitude in the resonance condition, the exact gain of an FPC antenna with a dimension of 1.5λ0 or more can be obtained through the equation.
IV. Conclusion
In this paper, we presented a gain equation for an FPC antenna with a finite dimension. The previous equation for the gain of an FPC antenna (which only accounted for an infinite dimension) was modified to include a function for a finite dimension. The modified equation was obtained through the curve fitting of the full-wave simulated results. As a result, the modified gain equation of an FPC antenna is valid when the dimension is larger than 1.5λ0. It will be helpful to be able to predict the gain of an FPC antenna.
Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2015R1A6A1A03031833).