|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 21(2); 2021 > Article |
|
Abstract
The accurate estimation of clutter covariance matrix (CCM) is essential in designing a radar detector/filter to suppress sea clutter. This estimation might not be easily accomplished because of the scarcity of valid training vectors adjacent to the range cell under test (CUT). We propose a new CCM estimation algorithm that is derived by modeling time-series clutter returns into a clutter Doppler spectrum in the frequency domain and exploiting mutual independence among spectral components. To justify its excellence over the conventional sample covariance matrix (SCM) algorithm, we design two filtersŌĆöa maximum signal-to-interference-plus-noise ratio (SINR)-based filter and a whitening filterŌĆöthat use the estimated CCMs and compare their performance in a numerically simulated sea clutter scenario. Comparisons are made by showing the eigenvector spectra of the estimated CCMs and the frequency responses and outputs of the filters. Moreover, SINRs at the target Doppler bin are examined and compared with a theoretical, analytically derived SINR.
Detecting a low velocity, small target in sea clutter, especially with low-grazing angle radar, is an important subject in maritime reconnaissance. The existence of sea clutter has been acknowledged as one of the major obstacles that hinders successful target detection. An ideal detector can inherently estimate clutter statistics, such as the clutter covariance matrix (CCM), the clutter power of cell under test (CUT), and range cells adjacent to the CUT, on the fly and apply those parameters to its signal processing component to maintain a constant false alarm rate (CFAR) [1, 2].
It has been said that the stationarity of clutter returns is as short as 100 ms at most [3]. Moreover, because of the heterogeneity of the sea environment, there are not enough training vectors that share the same CCM structure as a primary data vector [4]. These will make it difficult to estimate the CCM and consequently suppress clutter returns.
Many studies have been conducted to investigate the statistical properties of sea clutter, either by analyzing measurement data or by theoretical analysis. The statistical properties include the modeling of Doppler spectra of clutter returns, the spatial and temporal correlation of speckle and texture, clutter amplitude probability density function related with shape parameter and scale parameter, etc. [5, 6]. It turns out that a compound-Gaussian model has been found to be the best fit for sea clutter, especially at a low-grazing angle and high-resolution radar [7].
A detection scheme that works by suppressing clutter returns has been developed through the exploitation of the statistical properties of sea clutter. The generalized likelihood ratio test (GLRT) detector, referred to as a normalized matched filter (NMF), was derived in Gaussian noise, assuming the CCM structure was known [8]. The adaptive GLRT detector structure using the estimated CCM was derived and demonstrated to ensure the CFAR property with respect to the CCM [1].
There have been many studies proposing subspace-based clutter suppression techniques. Mathematical tools such as orthogonal projection (OP), singular value decomposition (SVD), principle eigenvector, etc. were applied to the constructed clutter subspace [9, 10].
In adaptive detectors, the estimation of the CCM has been of paramount importance in determining clutter suppression performance. The CCM in the NMF was replaced by the estimate of the sample covariance matrix (SCM) or by the normalized sample covariance matrix (NSCM) to guarantee the CFAR property with respect to the CCM or to the statistics of the texture or clutter power [4, 11]. In [12], an eigen-analysis-based CCM estimation algorithm called the regularized estimation method was proposed, and it was accessed through the adaptive NMF. Through effectively setting regularization parameters, this method tackled the problem of the scarcity of training vectors. This problem has also been dealt with in the context of the space-time adaptive processing (STAP) algorithm. Knowledge-aided STAP algorithms were proposed in this context, utilizing a priori data for the clutter map rather than many training vectors [13, 14]. To adapt to a more heterogeneous environment, a single data set (SDS) STAP algorithm that does not use any training vectors was proposed [15].
In this paper, we propose a new CCM estimation algorithm that does not require many training vectors and compare it with the conventional SCM-based algorithm, paying attention to the performance variation, which depends on the number of training vectors.
This paper is organized as follows. In Section II-1, we present the modeling of the sea CCM using discrete Fourier transform (DFT). In Section II-2, we propose a new CCM estimation algorithm. To compare it with the conventional SCM, two filtersŌĆöa maximum signal-to-interference-plus-noise ratio (SINR)-based filter and a whitening filterŌĆöusing the CCM estimates are introduced and analyzed in Section III-1 and Section III-2. In Section IV, through numerical simulations, we review the performance of the proposed algorithm, showing the two filtersŌĆÖ outputs. Finally, our conclusions are stated in Section V.
We consider a shipborne radar scenario where a radar makes N consecutive pulse transmissions and corresponding receptions during period T into a radar scene. To focus on sea CCM modeling, the target signature in the radar scene is neglected in this section.
Let cj[n] denote a clutter return of the jth range cell for the nth pulse. For N consecutive transmissions, we obtain the clutter return vector of the jth range cell, {cj[n]}(n = 0, 1, ┬Ę┬Ę┬Ę, N ŌłÆ 1). Let
{ C j [ k ] } ŌĆē ( k = - N 2 , ŌĆ” , N 2 - 1 ) f k = k N T
Eq. (1) can be rewritten in vector notation as
where cj Ōłł ŌäéN├Ś1 denotes cj ŌēĪ [cj[0], ŌĆ”, cj[NŌłÆ1]]T(superscript T denotes transpose) and for notational simplicity, rj,k is used in place of Cj[k]. Meanwhile, uk in Eq. (2) denotes
It is noted that uk Ōłł ŌäéN├Ś1 is, in fact, a Doppler steering vector of
f k = k N T
where nj is a complex additive white Gaussian noise vector. Using Eq. (2) and the statistical independence between cj and nj, the theoretical covariance matrix for vj, i.e., Rj Ōłł ŌäéN├ŚN, is expressed as
When manipulating Eq. (5), we use the orthogonality uk ŌŖź um for k ŌēĀ m and uk ŌŖź nj. According to [16], a collection of random variablesŌĆönamely, ╬│j,ksŌĆöcan be assumed to be mutually independent, having zero mean. That is,
where ╬┤k,m is the delta function defined as ╬┤k,m = 1 for k = m and ╬┤k,m = 0 otherwise.
where
╬Ę j , k 2 = E ŌĆē [ | ╬│ j , k | 2 ] f k = k N T
Rj in Eq. (7) can be rewritten as the form of the eigen-decomposition, that is,
where
U = [ u 1 u 2 ŌĆ” u N ]
Let R╠āj denote an estimate for Rj obtained by the SCM, which used to be a primary choice for CCM estimation. R╠āj is then expressed as
where L is the number of valid training vectors adjacent to the CUT and vl is the interference vector at the lth range cell.
Because of a finite number of training vectors, R╠āj cannot be ideally eigen-decomposed, as expressed in Eq. (8).
Let zl be the DFT of vl. zl can then be written as
In Eq. (10),
D = 1 N [ d - N 2 , ŌĆē d - N 2 + 1 , ŌĆ” , d N 2 - 1 ] T
Let
C j = [ ╬│ j , - N 2 ╬│ j , - N 2 + 1 Ōŗ» ╬│ j , N 2 - 1 ] T z l = 1 N ( C l + n l ŌĆ▓ ) n l ŌĆ▓ = 1 N D H n l
If there were an infinite number of training vectors available,
N L Ōłæ l z l z l H
The off-diagonal terms of the matrix in Eq. (13) should theoretically be zero because of the mutual independence of ╬│j,ks, as mentioned in Eq. (6). Although
N L Ōłæ l z l z l H
where Ōłś denotes the Hadamard product.
In summary, the proposed CCM estimation procedures are described as follows: i) obtaining a collection of training vector vls from the range bins adjacent to the CUT, ii) obtaining zls by taking the DFT of vls, iii) calculating
( N L Ōłæ l z l z l H ) Ōłś I D ŌĆē { ( N L Ōłæ l z l z l H ) Ōłś I } ŌĆē D H
We now consider a scenario of the presence of a moving target in the target scene. Since we are concerned with a case with a short observation interval, the target is assumed to have a constant Doppler frequency.
Let the clutter power only reside in [ŌłÆp1, p2] in the k domain. ╬╗j,k in (8) is then expressed as
In this section, we intend to design an adaptive filter that maximizes the output SINR, which hereafter will be referred to simply as the max SINR filter. In this case, for the desired Doppler steering vector sr with unity intensity, optimum weight wj,r becomes [17]
For k ŌēĀ r, sr is orthogonal to uk. In this case, wj,r is expressed as
Let the target Doppler frequency be fq, i.e., k = q. In this case, the received radar return from the jth range cell, xj, can be expressed as
where ╬Čj is the target reflectivity. ╬Čj is assumed constant in the following derivation because the change in target reflectivity for short processing intervals might be negligible. To examine the SINR of the filter output at the target bin, that is, the qth Doppler bin, we let fq be located somewhere within the clutter PSD, i.e., ŌłÆp1 Ōēż q Ōēż p2. The max SINR filter output at fr, namely, yj,r, then becomes
where ╬▓r = N╬Ęj,r2 + Žā2. The output SINR at the qth Doppler bin becomes
In deriving Eq. (20), we use the mutual independence between ╬│j,q and
u q H n j | ╬Č j | 2 E ŌĆē [ | ╬│ j , q | 2 ] = | ╬Č j | 2 ╬Ę j , q 2
Now, we examine the change in clutter power before and after filtering at the target-free bins. Let the rth Doppler bin be one out of the target-free region, that is, r ŌēĀ q and ŌłÆp1 Ōēż r Ōēż p2. Employing some manipulations, the clutter power at the rth Doppler bin, which is the mean square value of yj,r, E[|yj,r|2], is expressed as
1 N ╬Ę j , r 2 + Žā 2
In this section, we introduce the whitening filter, whose weight is dictated by
w j , r = R j - 1 2 s r w j , r = R j - 1 s r
Following the same procedures leading to Eq. (19) in Section III-1, the whitening filter output at fr, yj,r, is
where ╬▓r = N╬Ęj,r2 + Žā2, which is defined the same way it was in Eq. (19). As expected, at the target-free bins where r ŌēĀ q, the mean square value of yj,r in (21) becomes approximately 1, which implies that the interference PSD is whitened. The SINR at the qth target Doppler bin is approximately
N | ╬Č j | 2 N ╬Ę j , q 2 + Žā 2
Let us compare two filter outputs in terms of the interference suppression at the target-free bins. First, for the clutter-plus-noise bins in which r ŌēĀ q and ŌłÆp1 Ōēż r Ōēż p2, the E[|yj,r|2]s of the max SINR filter and the whitening filter are approximately
1 N ╬Ę j , r 2 1 N ╬Ę j , r 4 1 ╬Ę j , r 2
, respectively. Thus, depending on whether N╬Ęj,r2 is greater than 1, one filter outperforms the other.
We next examine two filter outputs at the noise-only Doppler bins that do not include clutter components. Employing some calculations, the output noise power E[|yj,r|2]s of the max SINR filter and the whitening filter are approximately
1 Žā 2 1 ╬▓ r N ╬Ę j , r 2 + Žā 2 Žā 2
To conclude, the whitening filter is generally more advantageous than the max SINR filter in that it outperforms noise suppression in the noise-only region while providing comparable results in terms of SINR at the target bin and in the extent of clutter suppression in the clutter plus noise region. In addition, it provides interference whitening in the target-free region, which may simplify the CFAR algorithm that will be applied to the filter output.
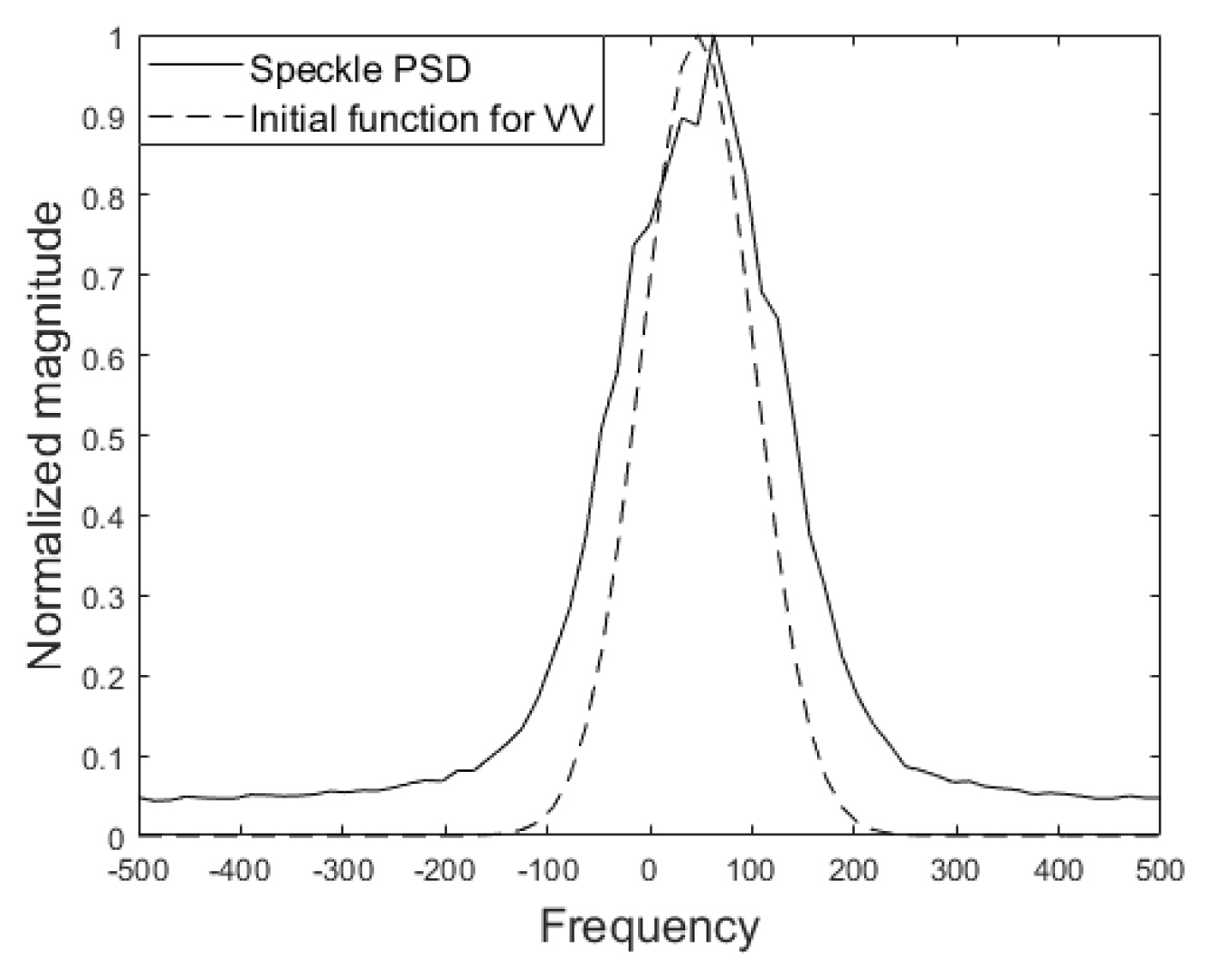
Before delving into the simulation details, we will briefly describe how the sea clutter returns were simulated. We essentially applied the procedure proposed in [5, 18] and simulated two kinds of clutter returns, VV polarized and HH polarized data, for 64 consecutive pulse transmissions. To simulate VV polarized data, the following steps are taken. Since the clutter spectrum in VV polarization is known to resemble a Gaussian function, we tried to assign the mean Doppler frequency and the spectrum width of the Gaussian function that characterize the function shape. To do this, we assumed that the wind speed is 12.5 m/s, operating frequency is 3 GHz, antenna look angle relative to the wind direction is 0┬░, relative texture value is 1, and platform-induced Doppler frequency is 0 Hz. With the parameter values assumed, the mean Doppler frequency of the Gaussian function becomes roughly 50 Hz. Its spectrum width was made arbitrarily large such that a moving target signature resides within the clutter spectrum. If a radar platform has motion, the platform-induced Doppler frequency is no longer 0 Hz, and a shift in the mean Doppler frequency is created. We will deal with this nonzero Doppler scenario in a later part of this section. For the chosen function shape, we next obtained the autocorrelation function by taking the inverse DFT (IDFT) of the Gaussian function. The sample values of the autocorrelation function were used as the finite impulse response (FIR) filter weights. As the input sequence to the FIR filter, we used a sequence of complex samples whose in-phase and quadrature components are random variables with zero mean and a variance of one-half. The output sequence of the FIR filter corresponds to the time-series clutter/speckle return data in VV polarization. We used the same texture value for the 64 clutter speckle components, as the interval is relatively short. The dashed line in Fig. 1 shows the initially chosen Gaussian-shaped Doppler spectrum. Following the afore-mentioned procedures, we generated 25 sets of the time-series speckle data cj[n] (n = 0, ┬Ę┬Ę┬Ę, 63), which is the output of the FIR filter. The solid line in Fig. 1 shows an ensemble average of |Cj[k]|2, which is the clutter PSD.
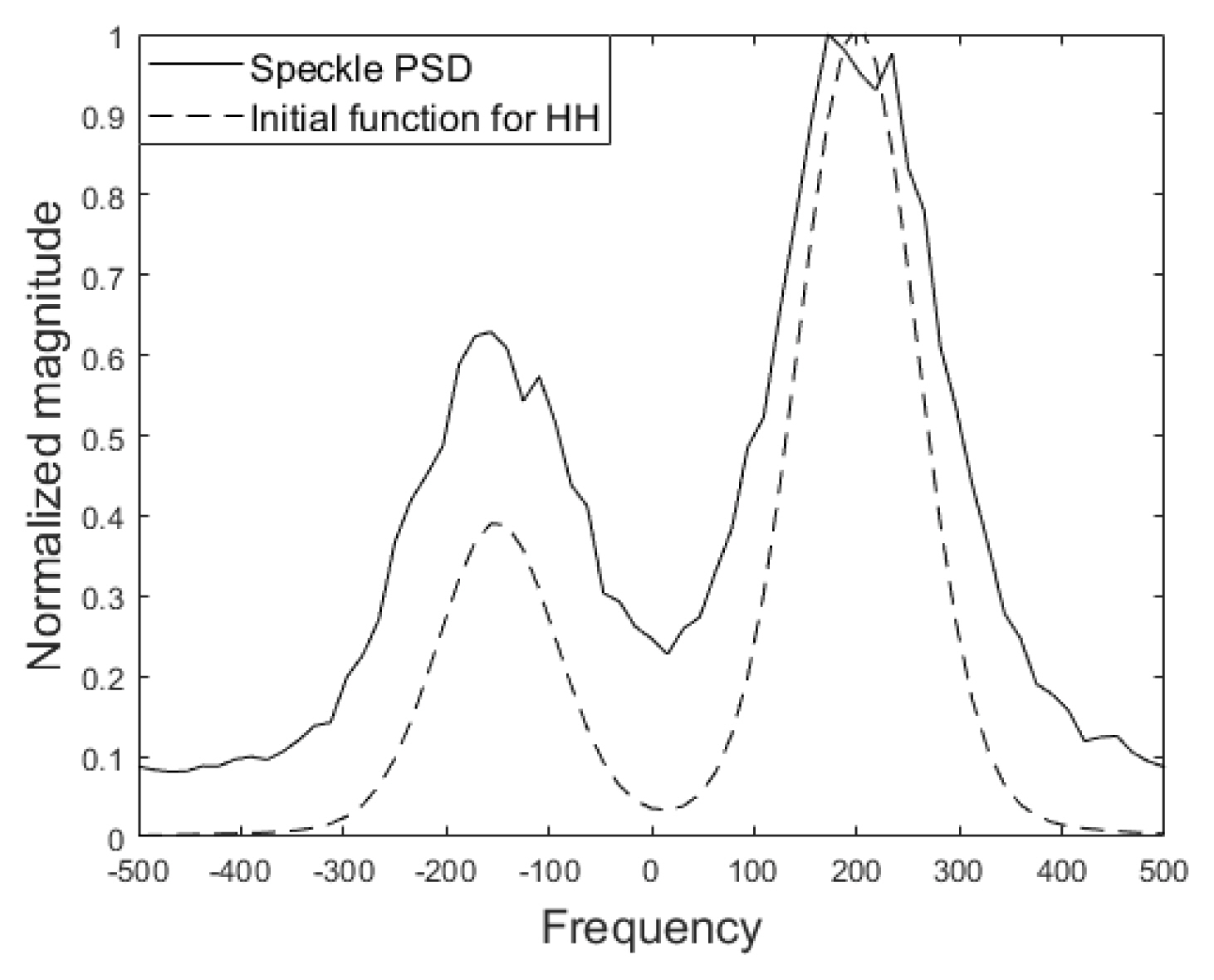
To simulate HH polarized return data, we first determine a Lorentzian function characterized by a small number of mean Doppler frequencies. We arbitrarily chose two mean Doppler frequencies, ŌłÆ150 Hz and 200 Hz. We next obtained the speckle Doppler function by convolving the Lorentzian function with an arbitrarily chosen Gaussian function. Since HH polarization returns are related to scatterers moving faster than Bragg scatterers, the typical function shape of the Doppler spectrum cannot be specified in such a way as to associate it with sea state and radar parameters. Thus, we do not enumerate the associated parameter values. For a given Doppler function, the rest of the procedure to simulate the time-series speckle return data is the same as before. The dashed line and the solid line in Fig. 2, respectively, show the initially chosen Doppler function and the PSD of the simulated HH polarized speckle data.
The first scenario concerns a short interval case of 64 radar returns in VV and HH polarization. A shipborne radar with a single transceiver operating at 3 GHz sends a sequence of pulses at 1 kHz of pulse repetition frequency (PRF). Within the target scene, there exists a moving target whose arbitrarily chosen Doppler frequency is 109 Hz. Considering the short interval, we assumed the target reflectivity was constant.
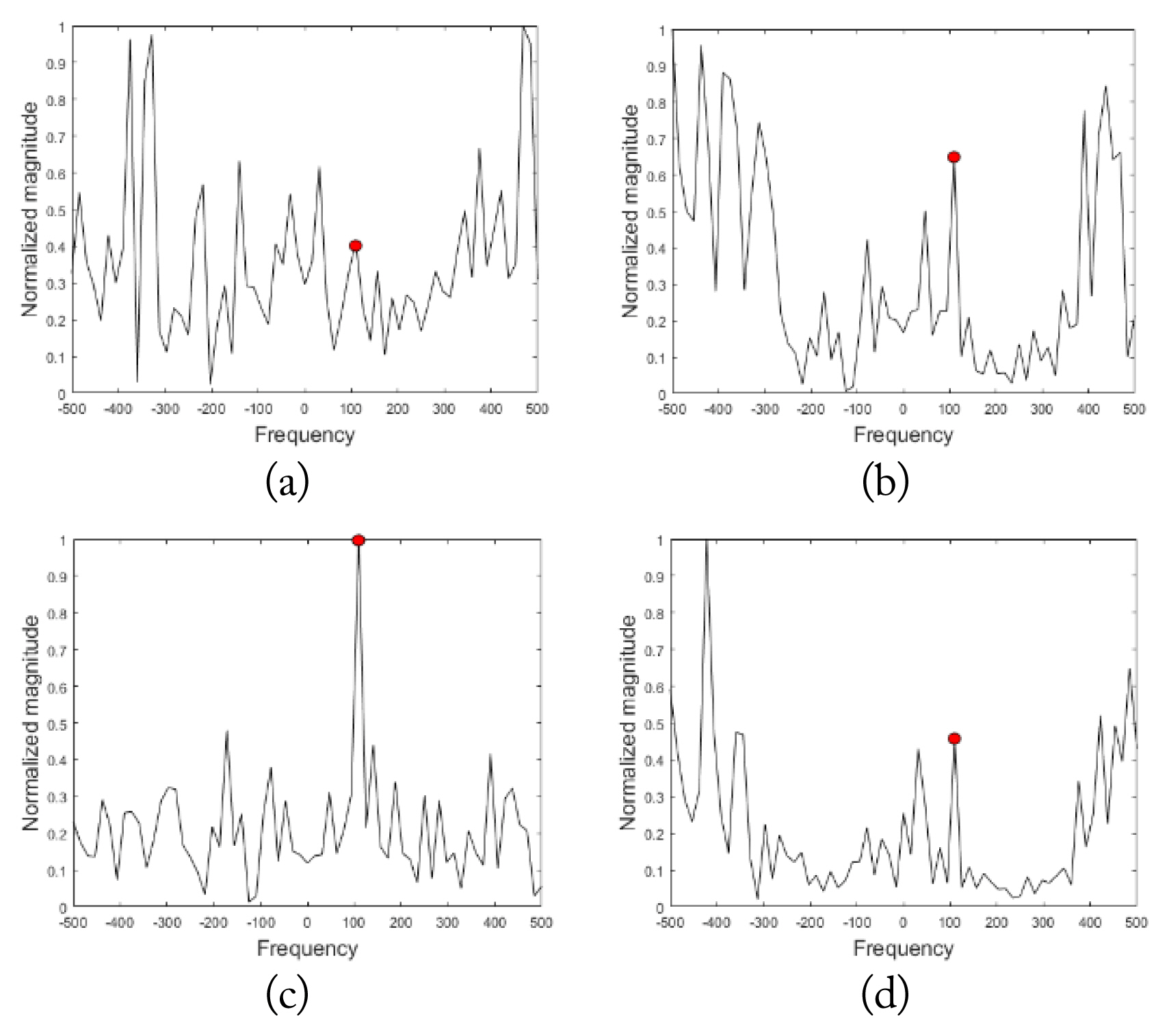
To calculate R╠āj using the SCM shown in Eq. (9) with the VV polarized data, we used 25 training vectors adjacent to the CUT. We next decomposed R╠āj into eigenvectors and eigenvalues. For all eigenvectors, we took the DFT and obtained their spectra. Fig. 3(a) shows the spectra arranged in such a manner that the spectrum of an eigenvector associated with a larger eigenvalue lay to the left of the x axis. We next applied the proposed algorithm to obtain R╠éj. Fig. 3(b) shows the plots of the spectra of the eigenvectors in R╠éj, which are arranged as in Fig. 3(a). We note that from the spectra shown in Fig. 3(b), the eigenvectors look to have a form of a Doppler steering vector of a single frequency, which is particularly apparent in the eigenvectors associated with larger eigenvalues. In order to determine the results that could be achieved if there were a sufficient number of training vectors, we arbitrarily generated 250 training vectors, calculated the R╠āj using the SCM, and finally obtained the eigenvector spectra shown in Fig. 3(c). More eigenvectors with larger eigenvalues appear to have the form of Doppler steering vectors of a single frequency. Fig. 3(d) is the plot of the eigen vector spectra obtained with the HH polarized data by applying the proposed method. Two dominant Doppler frequencies can be observed in the spectra of the eigenvectors associated with the large eigenvalues.
We next compared the frequency responses of the four filters constructed with CCM estimates by the VV polarized data. For convenience, three of these filtersŌĆöwhose weights are R╠ājŌłÆ1sr, R╠éjŌłÆ1sr, and
R ^ j - 1 2 s r
We next added a target signature to the generated interference, VV polarized data plus additive noise, and examined the filter outputs. The target return power was set to be small enough that the input signal-to-clutter ratio (SCR) and input clutter-to-noise ratio (CNR) were ŌłÆ27 dB and 20 dB, respectively. As shown in Fig. 5(a), the target peak could not be observed at the target Doppler bin of filter A. The target peak could be observed at the right Doppler frequency in Fig. 5(b), (c), and (d), which are the outputs of filter B, filter C, and filter D, respectively. The target peak shown in Fig. 5(c) looked more dominant because the interference in the target-free region was whitened.
Fig. 6(a)ŌĆō(d) show the outputs of filter A, filter B, filter C, and filter D, respectively, for the HH polarized data scenario. We may easily observe the same results as we did in the VV polarization case.
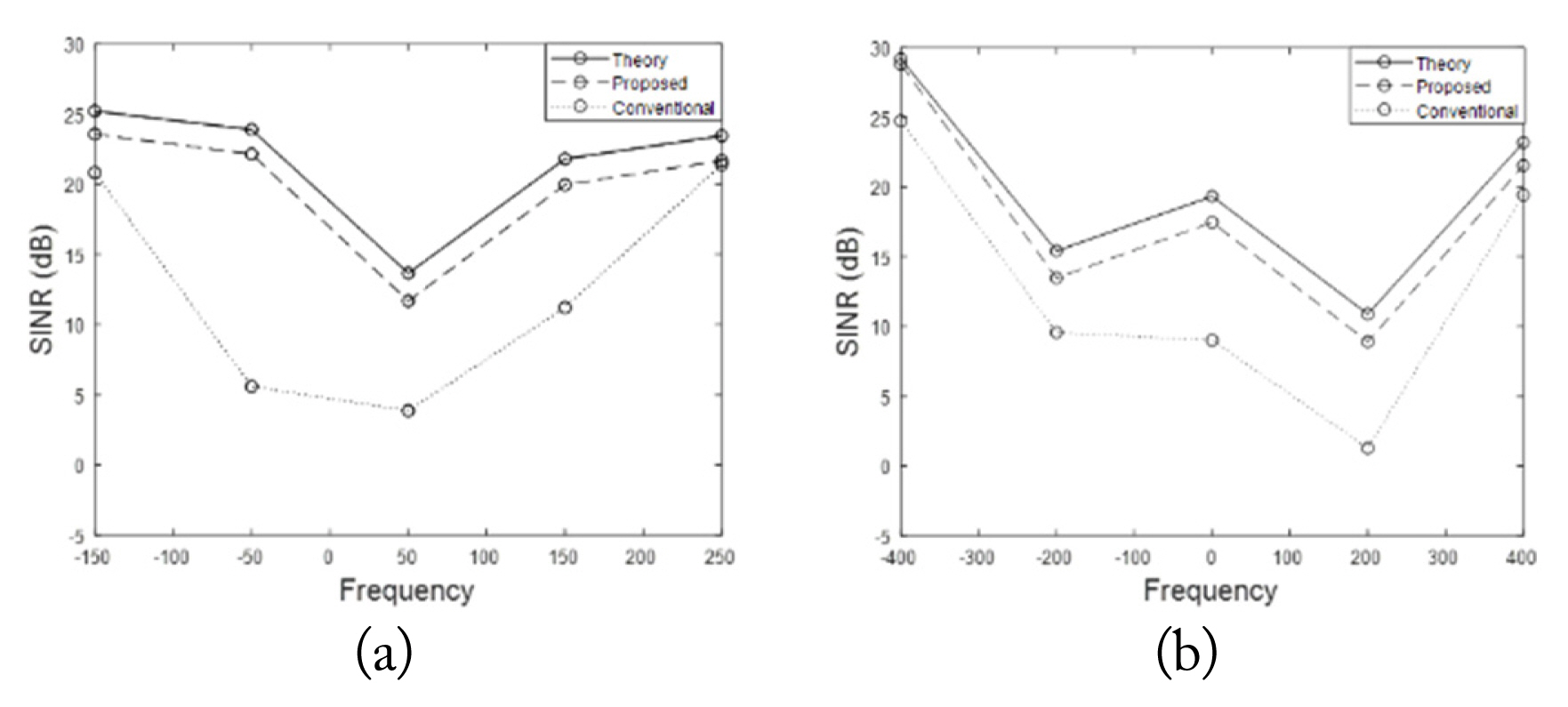
As mentioned earlier, the platform-induced Doppler frequency tends to shift the mean Doppler frequency of the clutter spectrum [18]. To reflect this aspect, we examined the filter outputs, moving around the moving target Doppler frequency while the clutter spectrum remained fixed. From a radar detector standpoint, this is basically equivalent to shifting the clutter mean Doppler frequency. Fig. 7(a) and (b) denote three SINRs obtained from the VV and HH polarized data, respectively.
The three SINR curves shown in Fig. 7 are the theoretical SINR curve and two other SINR curves obtained with the CCM estimates by the proposed and the conventional/SCM method, respectively. Calculation of SINRs was made at arbitrarily selected different Doppler frequencies in either the clutter plus noise region or the noise-only region of the clutter spectrum. As the theoretical SINR was obtained by Eq. (20), that is, by using a true CCM, it must put a ceiling on the SINR. For both the VV and the HH polarized data, the SINRs by the proposed method are closer to the theoretical SINRs than are the SINRs by the conventional method. This is quite obvious in the clutter plus noise region (see Figs. 1 and 2), which implies that the filter designed with the CCM from the proposed method effectively suppresses clutter. However, no noticeable difference among the three SINRs in the noise-only region can be observed, as the filter performance has no effect in this region.
In this paper, we proposed a CCM estimation algorithm in a sea clutter environment. To develop the algorithm, we modified the time-series clutter returns into the frequency domain clutter spectrum and exploited the mutual independence among the complex-valued Doppler spectral components. To compare the proposed algorithm with the SCM algorithm, two filtersŌĆöthe max SINR filter and the whitening filterŌĆöthat require the CCM were used. We first analytically derived the SINR at the target bin and the clutter suppression ratio in clutter and noise-only regions. Next, we numerically simulated sea clutter, applied the conventional and proposed estimation algorithms, and examined the outputs of the filters designed with the estimated CCMs. Comparisons were made by showing the eignvector spectra of the estimated CCMs and the frequency responses and outputs of the filters. Moreover, SINRs at target Doppler bins were examined with a theoretical, analytically derived SINR.
The filter using the proposed CCM estimate, regardless of the filter type, always showed better performance in suppressing clutter than the filter using the SCM estimate. Moreover, the whitening filter was more advantageous, especially in the noise-only region.
Acknowledgments
This work was supported by a Research Grant from Kwangwoon University in 2020 and by the Agency for Defense Development (No. UD170020FD).
Fig.┬Ā3
Spectra of eigenvectors. (a) CCM estimate by SCM (25 training vectors; VV). (b) CCM estimate by proposed algorithm (VV). (c) CCM estimate by SCM (250 training vectors; VV). (d) CCM estimate by proposed algorithm (HH).
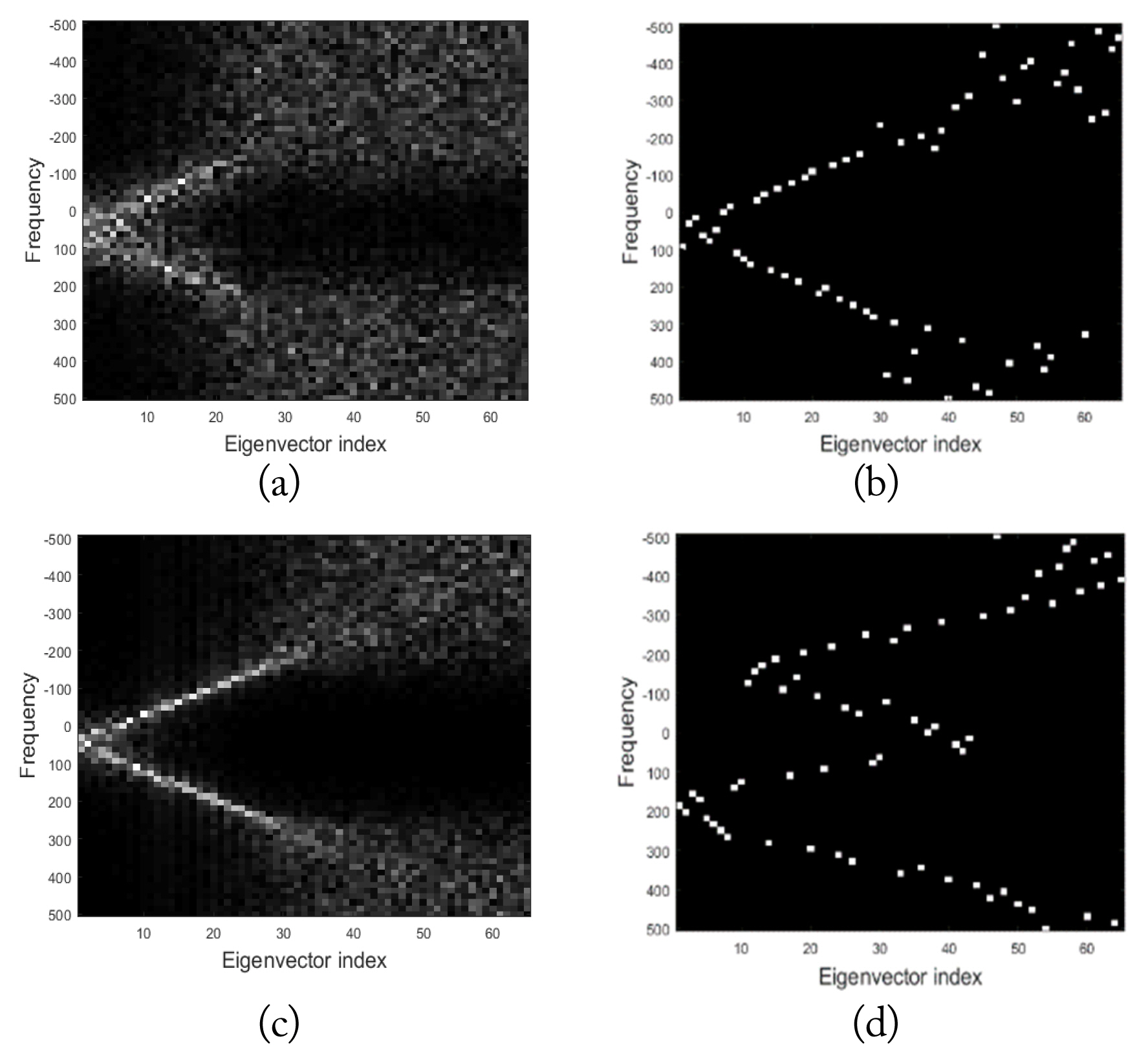
Fig.┬Ā4
(a) Frequency response of filter A. (b) Frequency response of filter B. (c) Frequency response of filter C. (d) Frequency response of filter D.
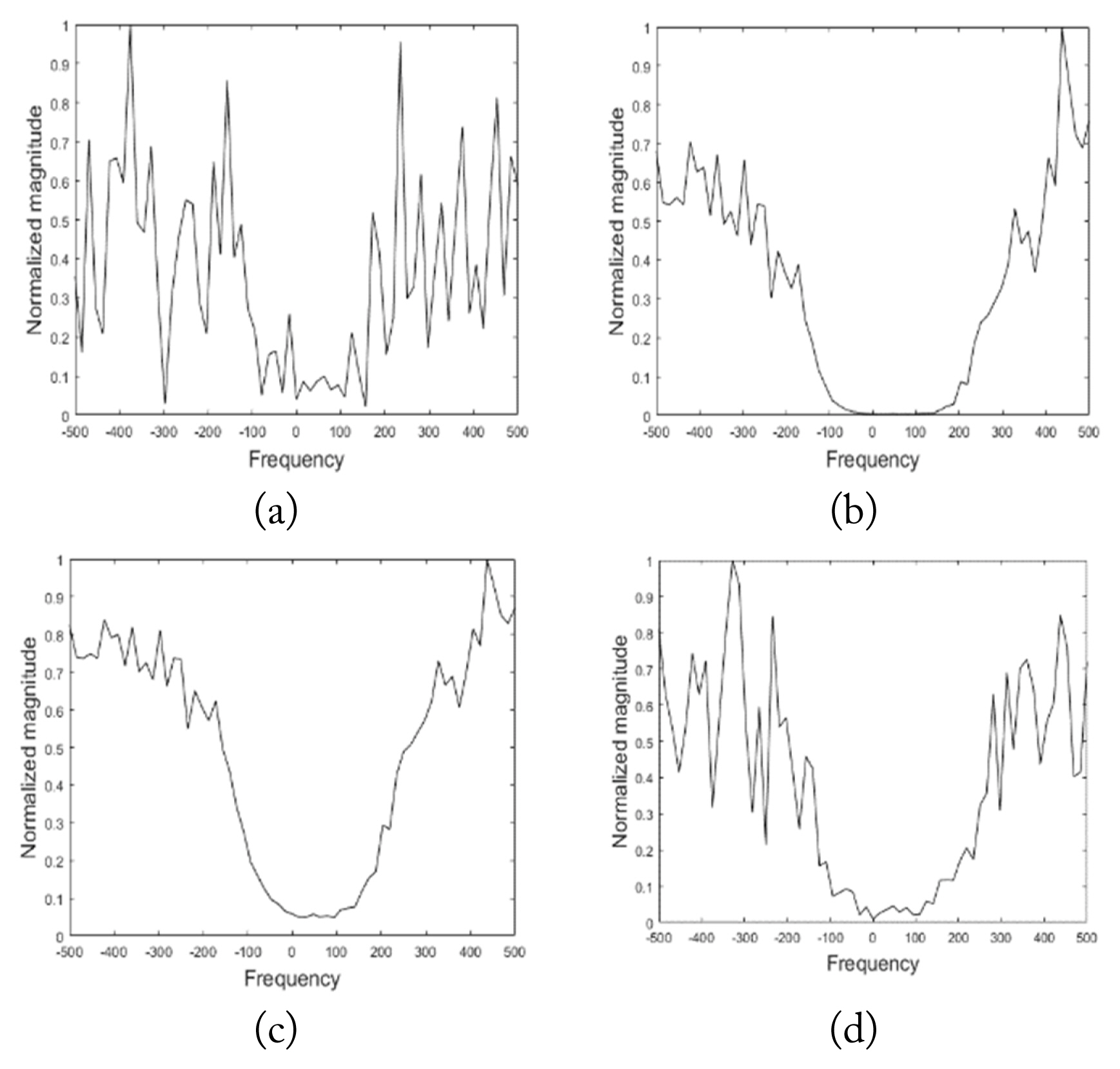
Fig.┬Ā5
Filter outputs in VV polarization. (a) Output of filter A. (b) Output of filter B. (c) Output of filter C. (d) Output of filter D.

References
1. EJ Kelly, "An adaptive detection algorithm," IEEE Transactions on Aerospace and Electronic Systems, vol. AES-22, no. 2, pp. 115ŌĆō127, 1986.

2. E Conte, M Longo, M Lops, and SL Ullo, "Radar detection of signals with unknown parameters in K-distributed clutter," IEEE Proceedings F (Radar and Signal Processing), vol. 138, no. 2, pp. 131ŌĆō138, 1991.

3. PL Shui and YL Shi, "Subband ANMF detection of moving targets in sea clutter," IEEE Transactions on Aerospace and Electronic Systems, vol. 48, no. 4, pp. 3578ŌĆō3593, 2012.

4. M Greco, P Stinco, and F Gini, "Impact of sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance," IEEE Transactions on Aerospace and Electronic Systems, vol. 46, no. 3, pp. 1502ŌĆō1513, 2010.

5. S Watts, "Modeling and simulation of coherent sea clutter," IEEE Transactions on Aerospace and Electronic Systems, vol. 48, no. 4, pp. 3303ŌĆō3317, 2012.

6. M Greco, F Gini, and M Rangaswamy, "Statistical analysis of measured polarimetric clutter data at different range resolutions," IEEE ProceedingsŌĆōRadar, Sonar and Navigation, vol. 153, no. 6, pp. 473ŌĆō481, 2006.

7. E Conte, MD Bisceglie, C Galdi, and G Ricci, "A procedure for measuring the coherence length of the sea texture," IEEE Transactions on Instrumentation and Measurement, vol. 46, no. 4, pp. 836ŌĆō841, 1997.

8. E Conte, M Lops, and G Ricci, "Asymptotically optimum radar detection in compound-Gaussian clutter," IEEE Transactions on Aerospace and Electronic Systems, vol. 31, no. 2, pp. 617ŌĆō625, 1995.

9. MWY Poon, RH Khan, and S Le-Ngoc, "A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar," IEEE Transactions on Signal Processing, vol. 41, no. 3, pp. 1421ŌĆō1425, 1993.

10. SP Sira, D Cochran, A Papandreou-Suppappola, D Morrell, W Moran, and S Howard, "A subspace-based approach to sea clutter suppression for improved target detection," In: Proceedings of 2006 40th Asilomar Conference on Signals, Systems and Computers; Pacific Grove, CA. 2006, pp 752ŌĆō756.

11. E Conte, M Lops, and G Ricci, "Adaptive detection schemes in compound-Gaussian clutter," IEEE Transactions on Aerospace and Electronic Systems, vol. 34, no. 4, pp. 1058ŌĆō1069, 1998.

12. A Kammoun, R Couillet, and F Pascal, "Optimal design of the adaptive normalized matched filter detector using regularized Tyler estimators," IEEE Transactions on Aerospace and Electronic Systems, vol. 54, no. 2, pp. 755ŌĆō769, 2018.

13. W Melvin, M Wicks, P Antonik, Y Salama, P Li, and H Schuman, "Knowledge-based space-time adaptive processing for airborne early warning radar," IEEE Aerospace and Electronic Systems Magazine, vol. 13, no. 4, pp. 37ŌĆō42, 1998.

14. H Jeon, Y Chung, W Chung, J Kim, and H Yang, "Clutter covariance matrix estimation using weight vectors in knowledge-aided STAP," Electronics Letters, vol. 53, no. 8, pp. 560ŌĆō562, 2017.

15. ZY Chen, Y Zhou, LR Zhang, Q Li, and YB Gu, "A robust single data set-STAP algorithm," In: Proceedings of IET International Radar Conference; Hangzhou, China. 2015.

16. S Theodoridis and R Chellappa, Academic Press Library in Signal Processing: Communications and Radar Signal Processing. New York, NY: Academic Press, 2014.
17. JR Guerci, Space-Time Adaptive Processing for Radar. Norwood, MA: Artech House, 2003.
Biography

Sanghyun Choi received B.S. and M.S. degrees in electric wave engineering from Kwangwoon University, Seoul, Korea, in 2017 and 2019, respectively. He currently works at Korea Aerospace Industries Ltd., Sacheon, Korea, where he is engaging in research on and development of satellite electrical systems. His research interests include the generation and suppression of sea clutter and moving target imaging in a MIMO radar environment.
Biography

Hoongee Yang received a B.S. degree in electronic engineering from Yonsei University, Seoul, Korea, in 1985 and M.S. and Ph.D. degrees in electrical and computer engineering from the State University of New York at Buffalo, Amherst, NY, in 1987 and 1992, respectively. Since 1993, he has been with the Department of Electronic Convergence Engineering, Kwangwoon University, Seoul, Korea. His current research interests are radar signal processing, array signal processing, and SAR/ISAR imaging.
Biography

Jimin Song received B.S. and M.S. degrees in electric wave engineering from Kwangwoon University, Seoul, Korea, in 2017 and 2019, respectively. He is currently working in the Electronics & Software Development Department of Renault Samsung Motors, Yongin, Korea, where he is being engaged in the development of a control logic for safety & seat systems. His current interests are radar imaging techniques and sensor fusion using radar and vision data.
Biography

Hyeonmu Jeon received a B.S. degree in electronic engineering and a Ph.D. degree in radio science and engineering from Kwangwoon University, Seoul, Korea, in 2017. Since 2017, he has been with the Radar Research Institute at Hanwha Systems, where he is currently a Senior Engineer. His main research interests are array signal processing, space time adaptive processing, and synthetic aperture radar.
Biography

Jongmann Kim received a B.S. degree in electronic and electrical engineering from Kyungpook National University, Daegu, Korea, in 2002 and an M.S. degree in electronic and electrical engineering from Pohang University of Science and Technology (POSTECH), Pohang, Korea, in 2004. Since 2005, he has been with the Agency for Defense Development (ADD), Daejeon, Korea, where he is currently a Principle Researcher. His current research interests include radar signals and data processing.
Biography

Yongseek Chung received his B.S., M.S., and Ph.D. degrees in electrical engineering from Seoul National University, Seoul, Korea, in 1989, 1991, and 2000, respectively. From 1991 to 1996, he was with the Living System Laboratory at LG Electronics. From 1998 to 2000, he was a Teaching Assistant in electrical engineering at Seoul National University. From 2001 to 2002, he was with Syracuse University, Syracuse, NY. From 2003 to 2005, he has been a faculty member with the Department of Communication Engineering, Myongji University, Kyunggi, Korea. He is currently a professor in the Department of Electronic Convergence Engineering, Kwangwoon University, Seoul, Korea. His current interests are radar signal processing and microwave imaging techniques.
- TOOLS