Numerical Accuracy of Finite-Difference Time-Domain Formulations for Magnetized Plasma
Article information
Abstract
The finite-difference time-domain (FDTD) has been widely used to analyze electromagnetic (EM) wave propagation in complex dispersive media. Over the past three decades, a variety of FDTD approaches for the EM wave propagation in magnetized plasma has been presented. In this work, we perform a comprehensive study on the numerical accuracy of four FDTD formulations for magnetized plasma including the JE convolution (JEC) method, the exponential time differencing (ETD) method, the H–J collocated auxiliary differential equation (ADE) method, and the E-J collocated ADE method. Toward this purpose, the numerical permittivity tensor of magnetized plasma in the four FDTD formulations are derived and then we analyze them to determine which approach can provide the best accuracy. It is found that the E-J collocated ADE method can lead to the best accuracy. Numerical examples awere performed to validate our investigations.
I. Introduction
The finite-difference time-domain (FDTD) method [1–5] has been popularly used to study various electromagnetic (EM) wave problems due to its accuracy, robustness, and simplicity. Over the past three decades, the FDTD method has been extended to simulate anisotropic dispersive media, including magnetized plasma. There are various FDTD formulations for EM analysis of magnetized plasma, including the JE convolution (JEC) method [6–9], exponential time differencing (ETD) method [10, 11], and auxiliary differential equation (ADE) method [12–14]. In the JEC method, recursive convolution is involved in the relation between the current density and electric field. The ETD method avoids the time-consuming recursive convolution based on an efficient first-order approximation. Simple arithmetic implementation is involved in the ADE method, which can also be straightforwardly extended to nonlinear dispersive media, unlike other methods [15, 16]. There are two particular implementations in the ADE method for EM analysis of magnetized plasma. First, in the H-J collocated ADE method, magnetic field (H), and current density (J) are collocated in the same time domain when discretizing J [12]. Second, in the E-J collocated ADE method, electric field (E), and J components are collocated simultaneously [13]. Unlike the H-J collocated ADE method, the stability condition of the E-J collocated ADE method is independent of the medium properties and remains the same as the Courant stability limit for free space [14].
We perform a comprehensive study on the numerical accuracy of four dispersive FDTD formulations for modeling magnetized plasma. For this purpose, we derive the numerical permittivity tensor of magnetized plasma in the different methods and compare them with the corresponding analytical counterpart. Numerical examples are employed to investigate the numerical permittivity tensor of the JEC, ETD, H-J collocated ADE, and E-J collocated ADE methods in detail.
II. Numerical Permittivity of Dispersive FDTD Formulations
In magnetized plasma, the governing equations are given by [14]
where νc is the collision frequency, ωp is the plasma frequency, ωb is the cyclotron frequency, and ɛ0 and μ0 are the permittivity and permeability of free space, respectively. Note that cyclotron frequency is a function of the static magnetic field. The cross-product terms in Eq. (3) can lead to anisotropy of plasma. Thus, EM wave behavior depends on the direction of the static magnetic field relative to the EM wave propagation direction. It is assumed that the external static magnetic field in Cartesian coordinates is parallel to the z-axis; then, the component equations of Eq. (3) can be written as
where Jx, Jy, and Jz are the current densities. Eqs. (4) and (5) indicate that two components of current density are coupled. Therefore, the update equations for polarization current density must be solved simultaneously. Moreover, for magnetized plasma, such as in the earth’s ionosphere, the electrons rotate about a steady magnetic field vector. Therefore, the plasma becomes nonreciprocal, and the scalar relationship between the electric flux density and electric field must be replaced by the tensor relation. The analytical permittivity tensor can be obtained using Eqs. (1), (4), and (5) as follows [17]:
Note that the z component of tensor permittivity is reciprocal because the external static magnetic field does not affect the wave behavior in that direction [15].
Due to the discrete nature of the FDTD technique, the numerical permittivity tensor of magnetized plasma in dispersive FDTD approaches is different from its analytical permittivity tensor. According to the standard FDTD method, the E field is defined at integer time steps and the H field is defined at half integer time steps. By applying the central difference scheme (CDS) to Eqs. (1) and (2), we have
where Δt indicates the FDTD time step size and the superscript indicates the FDTD time step. In what follows, Eqs. (9) and (10) are employed, unless specified otherwise. In addition, the tilde characters indicate their numerical counterparts.
1. JEC method
For time-harmonic dependence, the following frequency-domain relation can be derived from Eqs. (4) and (5):
where
In the time domain, the above equations can be expressed by convolution [6–9]:
where u(t) is the unit step function. Substitution Eq. (17) into Eqs. (15) and (16) yields the following equations:
Let us consider the numerical permittivity tensor of magnetized plasma in the JEC method. To derive the numerical permittivity tensor, using Yee’s notation and t = (n+1/2)Δt in Eq. (18), we get
At t = (n–1/2)Δt, we have
Substituting Eq. (21) into Eq. (20), we obtain
where
By using the Taylor series expansion of Eq. (22), we have
According to Eqs. (22) and (24), the following second-order approximation can be written as
Using a similar procedure, we have
By using plane-wave expansion [18, 19] and applying some mathematical manipulations, we have
with
Substituting Eqs. (27) and (28) into the plane-wave expansion version of Eq. (9) and then rearranging the resulting equation can lead to the following numerical permittivity tensor:
where
The numerical permittivity converges to analytical permittivity as the time-step size approaches zero.
2. ETD method
In this subsection, we derive the numerical permittivity tensor of magnetized plasma using the ETD method. In the ETD method, the discrete form for Eq. (4) can be written as [10, 11]
where
and
Substituting Eqs. (32) and (33) into (31) yields
Using a similar procedure
By utilizing plane-wave expansion and applying some mathematical manipulations, we have
Substituting Eqs. (36) and (37) into the plane-wave expansion version of Eq. (9) and then rearranging the resulting equation, we have the same Eqs. (29) and (30) with
Again, as the time step size approaches zero, the numerical permittivity converges to the analytical permittivity.
3. H-J collocated ADE method
In the H-J collocated ADE method, we can write [12]
Now, we use the plane-wave expansion again and have
Following the procedure described above, the numerical permittivity tensor is the same as Eqs. (29) and (30) with
Note that the collision and cyclotron frequencies are the same as the analytical ones.
4. E-J collocated ADE method
Unlike the other methods considered above, the current density vectors are collocated at the same time step and position of the electric field vectors in the E-J collocated ADE method. Therefore, the FDTD update equation for Ampere’s law can be written as
According to [13], the update equations of the current density in the E-J collocated ADE method can be written as
We use the plane-wave expansion again and have
The numerical permittivity tensor of magnetized plasma in the E-J collocated ADE method can be obtained by a similar procedure, and we have the same as Eqs. (29) and (30) with
Note that only the angular frequency has a numerical value different from the analytical one, which implies that the E-J collocated ADE method can lead to better results than the other methods considered in this study.
III. Numerical Examples
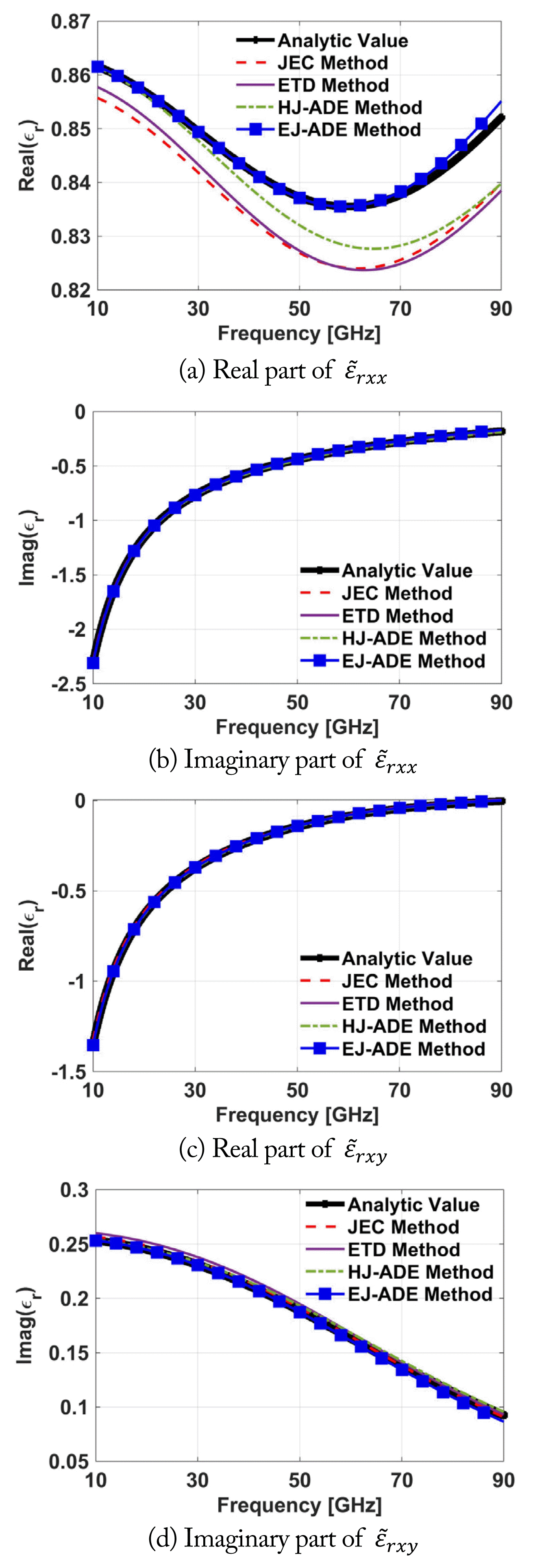
In this section, we investigate the numerical accuracy of the JEC, ETD, H-J collocated ADE, and E-J collocated ADE methods. We assume that the plasma frequency ωp=2π×50×109 rad/s, cyclotron frequency ωb = 3×1011 rad/s [20], and vc = 5×1011 Hz. The simulation frequency ranges from 10 to 90 GHz, and the spatial cell is Δz = 75 μm. The FDTD time size is Δt = 1.111 ps, which is temporal points per period (PPP) equal to 10.
Fig. 1 shows the numerical relative permittivity tensor of magnetized plasma. As shown in the figure, large differences between the analytical and numerical permittivity tensors in the JEC and ETD methods are observed because all four numerical parameters (ω̃,ṽc,ω̃b,ω̃p) are not the same as the analytical ones. The H-J collocated ADE method has two numerical values (ω̃,ω̃p) different from the analytical ones, but the E-J collocated ADE method has only one numerical value (ω̃) different from the analytical one. Therefore, the E-J collocated ADE method can yield the best numerical accuracy among the four FDTD methods considered in this study. Next, let us investigate the root-mean-square (RMS) error of the numerical relative permittivity in the four FDTD methods versus the FDTD time step size. The RMS error is defined as
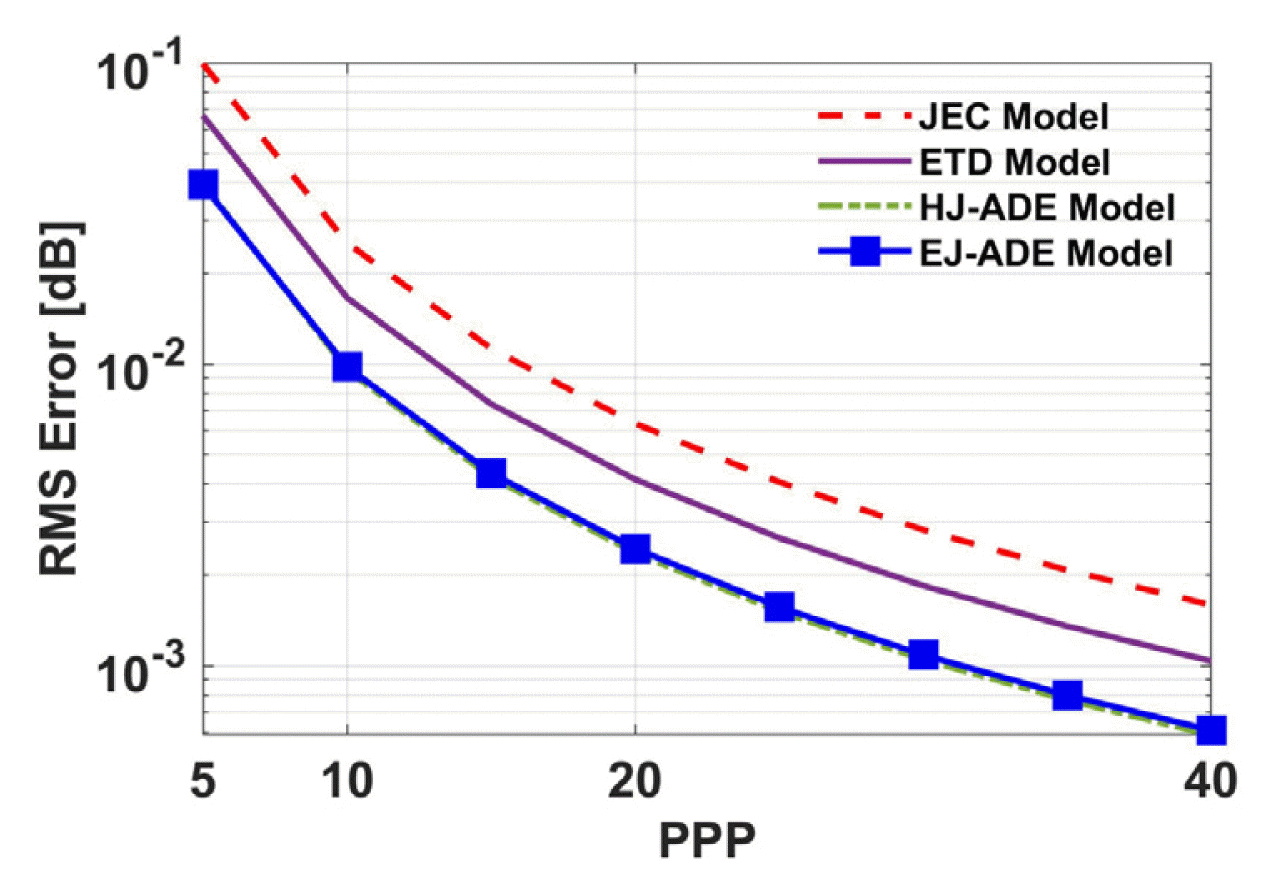
Here, ε̃r,ɛr,fa, and fb indicate the numerical relative permittivity, analytical relative permittivity, minimum frequency, and maximum frequency in the frequency range of interest.
Figs. 2 and 3 show the RMS error of the numerical relative permittivity tensor. As the time step size decreases (PPP increases), the RMS error decreases. Again, the E-J collocated ADE method yields the best accuracy.
IV. Conclusion
We investigated the numerical accuracy of various FDTD formulations for magnetized plasma. The exact expressions of the numerical permittivity tensor were derived, and the E-J collocated ADE method was found to yield the best accuracy. In addition, numerical examples were used to validate our investigation.
Acknowledgments
This research was supported by an Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2019-0-00098, Advanced and integrated software development for electromagnetic analysis) and by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1055444).
References
Biography

Jeahoon Cho received his B.S. degree in Communication Engineering from Daejin University, Pocheon, Rep. of Korea, and his M.S. and Ph.D. degrees in electronics and computer engineering from Hanyang University, Seoul, Rep. of Korea, in 2004, 2006, and 2015, respectively. From 2015 to August 2016, he was a postdoctoral researcher at Hanyang University. Since September 2016, he has worked at Hanyang University, where he is currently a research professor. His current research interests include computational electromagnetics and EMP/EMI/EMC analysis.

Min-Seok Park received his B.S. degree in Department of Electrical Engineering from Myongi University, Yongin, Rep. of Korea, in 2015, and his M.S. degree in electrical engineering from Hanyang University, Seoul, Rep. of Korea, in 2017. From 2018 to 2020, he participated in EM-Tech’s circuit and product development. He is currently pursuing a Ph.D. degree in electrical and computer engineering. His current research interests include computational electromagnetics, wave propagation, and multi-physics.

Kyung-Young Jung received his B.S. and M.S. degrees in electrical engineering from Hanyang University, Seoul, Rep. of Korea, in 1996 and 1998, respectively, and his Ph.D. degree in electrical and computer engineering from The Ohio State University, Columbus, USA, in 2008. From 2008 to 2009, he was a postdoctoral researcher at the Ohio State University, and from 2009 to 2010, he was an assistant professor at the Department of Electrical and Computer Engineering, Ajou University, Suwon, Rep. of Korea. Since 2011, he has worked at Hanyang University, where he is now a professor in the Department of Electronic Engineering. His current research interests include computational electromagnetics, bioelectromagnetics, and nanoelectromagnetics. Dr. Jung was a recipient of the Graduate Study Abroad Scholarship from the National Research Foundation of Korea, the Presidential Fellowship from The Ohio State University, the HYU Distinguished Teaching Professor Award from Hanyang University, and the Outstanding Research Award from the Korean Institute of Electromagnetic Engineering Society.