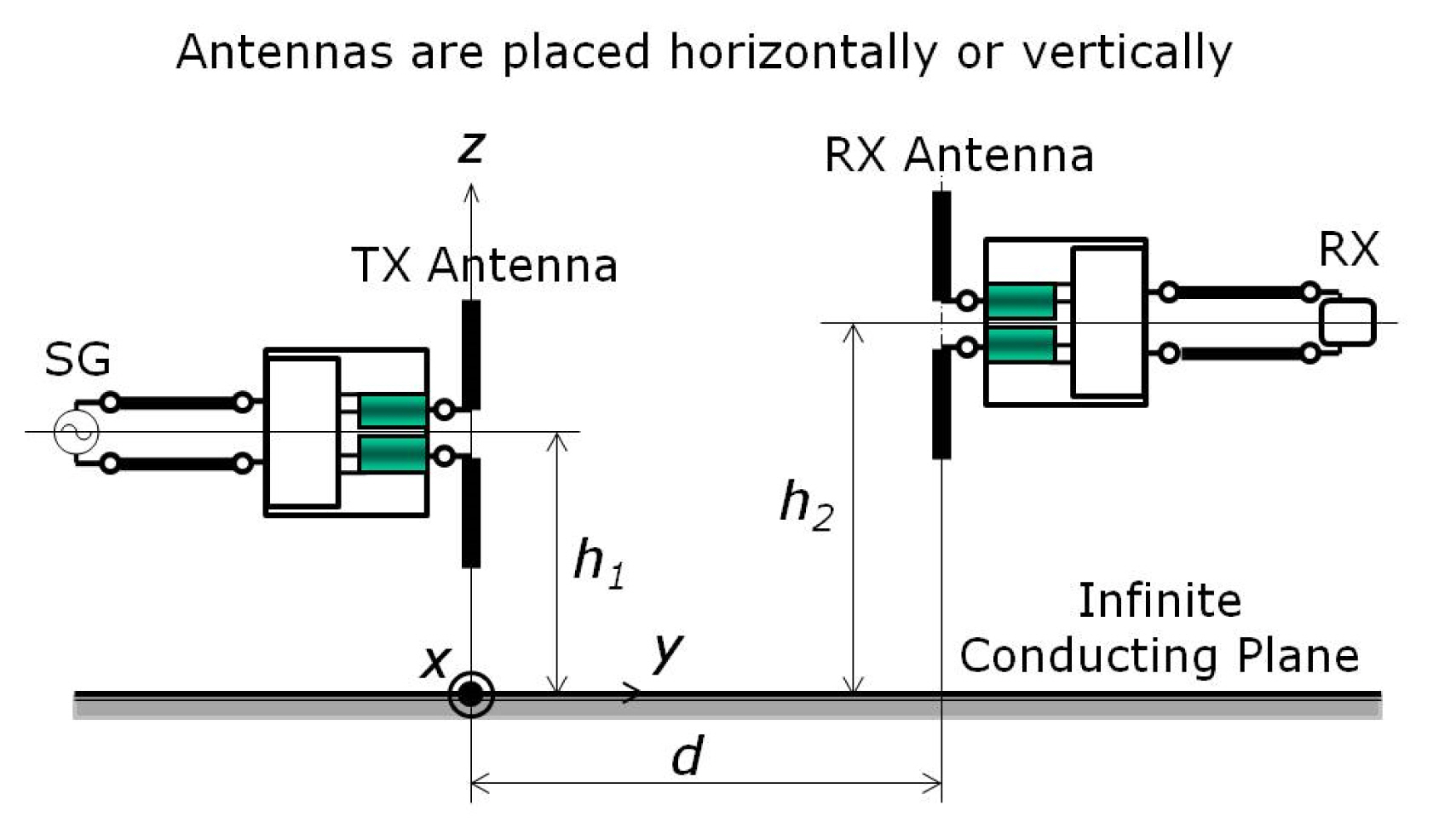
Fig. 1 shows the configuration of the SA measurement system using calculable dipole antennas with a 3-dB hybrid balun on the OATS. Two dipole antennas are located along the x-axis (horizontal polarization, HP) or the z-axis (vertical polarization, VP) above the ground plane with a TX antenna height of h₁ and RX antenna height of h₂. Further, d is the distance between the TX and RX antennas.

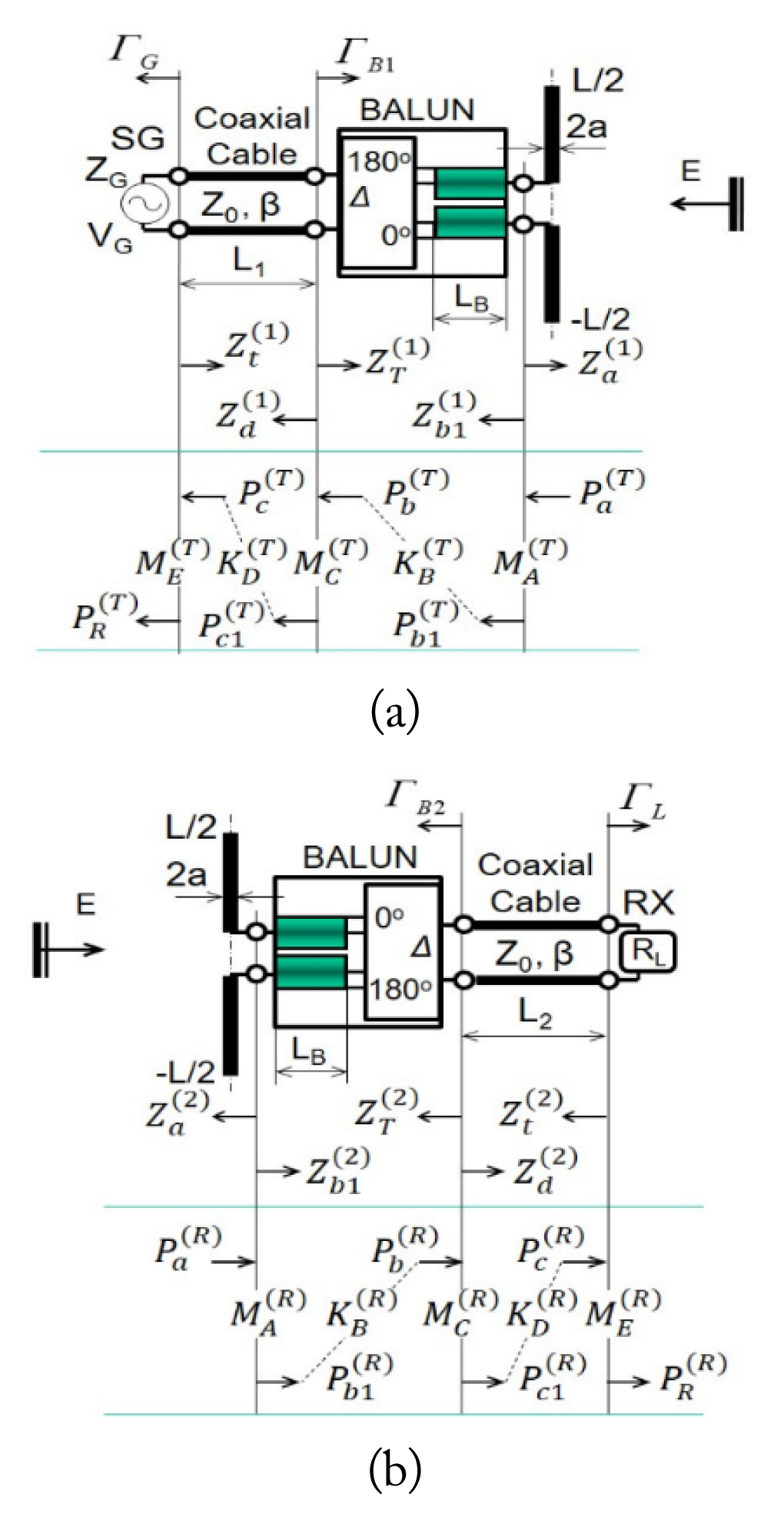
Fig. 2 shows the power mismatch and dissipative loss factors of the SA measurement system and the basic structure of the CalDA. The balun was designed so that its complex S-parameters could be easily measured. Two semi-rigid cables with a length of L_B from the 3-dB hybrid coupler are connected to the antenna terminal, as shown in Figs. 1 and 2. A 50-Ω load is connected to the sum port (∑) of the hybrid, and a matched measuring instrument is connected to the other port (Δ), using a coaxial cable with a length of L₂. The inner conductors of the two semi-rigid cables are connected to the balanced dipole elements. Their outer conductors are in contact with each other electrically (i.e., short-circuited) at the feeding point of the dipole elements.

The TX antenna is excited by a signal generator (SG), and the RX antenna receives the signal radiated by the TX antenna through the OATS, as shown in Fig. 2. The SA accounts for all power losses occurring between the RX and TX antennas over the ground plane. Two kinds of losses generally occur: conjugate mismatch losses and dissipative losses.

The CSA is defined as the minimum site power loss between the two antennas, including the baluns, as the RX antenna scans over a given height range. The CSA can be expressed in decibels in a simplified form [21]:

where Za(2)=Ra(2)+jXa(2) is the input impedance from the RX antenna terminal to the TX antenna and ZijA is the impedance parameters of the TX and RX antennas as a two-port network. Zb1(1)=Rb1(1)+jXb1(1) is the input impedance from the input terminal of the TX hybrid balun to the SG, and Zb1(2)=Rb1(2)+jXb1(2) is the input impedance from the input terminal of the RX hybrid balun to the receiver.

The expression of CSA can be evaluated by using impedance parameters of the TX and RX antennas. As shown in Appendix, the result is as follows:

Eq. (2) is the CSA expressed with antenna impedance parameters and balun impedances of the TX and RX parts. It is emphasized that Eq. (2) is a newly derived equation using the concepts of power mismatch and dissipative loss.

The theoretical NSA of an ideal OATS is defined as the normalized SA from CSA using AFs:

where AF₁ and AF₂ are the AFs for the TX and RX antennas, respectively. These include the mutual coupling effect between the ground plane and two antennas when TX and RX antennas are located for the measurement of the NSA. Note that the quantities in Eq. (3) are linear. All quantities in decibels appearing in the rest of the paper are given with (dB).

The theoretical NSA can be expressed in decibels as follows:

In relevant international standards, the theoretical NSA of an ideal OATS is defined as follows:

where AF_1FS and AF_2FS are the FSAFs of the TX and RX antennas, respectively. ΔAF_TOT is the mutual impedance correction factor [1]. The relevant parameters for NSA calculation are listed in Table 1.

If we use FSAFs for measurements of the NSA, the mutual impedance correction factor is necessary. In this paper, the theoretical NSA by the FSAFs, SA_FS, is normalized from the CSA by using the FSAFs.

Note that quantities in Eq. (6) are linear. In decibel form, Eq. (6) is expressed as follows:

In this case, an AF correction factor, ΔAF_TOT, is necessary to obtain the true NSA, as shown in Eq. (5).

From Eqs. (5) and (7), the theoretical NSA of an ideal site is expressed as follows:

The difference between the true AF (AF₁ and AF₂) and the FSAFs (AF_1FS and AF_2FS) is expressed as follows:

Hence, the total AF difference is expressed as follows:

This is known as the mutual impedance correction factor that appears in Eq. (5) and the ANSI C63.4 standard [1].

Therefore, the difference between the true NSA and NSA_FS is expressed as ΔNSA:

From Eqs. (4) and (7), ΔNSA is expressed as follows:

Therefore, the total mutual impedance correction factor ΔAF_TOT is the same value as −ΔNSA.

In order to consider the theoretical NSA, the AFs of the TX and RX antennas, AF₁ and AF₂, are needed to calculate the NSA. Fig. 3 shows the TX and RX antennas for the evaluation of the AFs. Note that the power loss parameters of the TX antenna part in Fig. 3(a) are different from those in Fig. 2 because the AF is defined in the receiving mode. To unify the AF representation, the TX and RX parts are represented by the superscripts T and R, respectively. For the RX part, Fig. 3(b) is the same as Fig. 2—i.e., Pa(R)=Pa(2),MA(R)=MA(2),Pb1(R)=Pb1(2), and so on.

The details of the CalDA analysis using the power mismatch and dissipative loss concepts are given in other studies [19, 20]. The desired AFs of the TX and RX antennas above a ground plane, AF₁(h₁, h₂, d) and AF₂(h₁, h₂, d), can be expressed as follows:

where he(1) and he(2) are the effective length of TX and RX antennas, respectively. Ra(1) is the input resistance from the TX antenna terminal to the RX antenna, Ra(2) is the input resistance from the RX antenna terminal to the TX antenna. R_G and R_L are the input resistance of the SG and receiver, respectively. The major parameters for AF calculation are listed in Table 2. AF0(T) and AF0(R) are the AFs when the SG and receiver are directly connected to the TX and RX antennas, respectively. MK(T) and MK(R) are the power dissipative loss and mismatch-loss factors and can be expressed as follows:

where ZijT and ZijR are the impedance parameters of the TX and RX baluns, respectively, as a two-port network.

Since the hybrid balun has a 100-Ω balanced port and a 50-Ω unbalanced port [19], MC(T)=MA(T) and KB(T)=1/MC(T) from ZT(T)=Za(T)/2 and Zb1(T)=2Zd(T) for the TX part. We also obtain MC(R)=MA(R) and KB(R)=1/MC(R) from ZT(R)=Za(R)/2and Zb1(R)=2Zd(R) for the RX part. Therefore, MK(T) and MK(R) are expressed as follows:

The true AF₁ and AF₂ values are different from the FSAFs (AF_1FS and AF_2FS). The AF₁ is also different from the AF₂ because the height of the TX antenna is fixed, but the RX antenna’s height is scanned above the ground plane.

As shown in Eqs. (9) and (10), the total AF difference between the true AF and the FSAF is expressed as follows:

The total AF difference ΔAF_TOT corresponds to the total AF correction factor and is known as the mutual impedance correction factor, as explained in Section II-3.

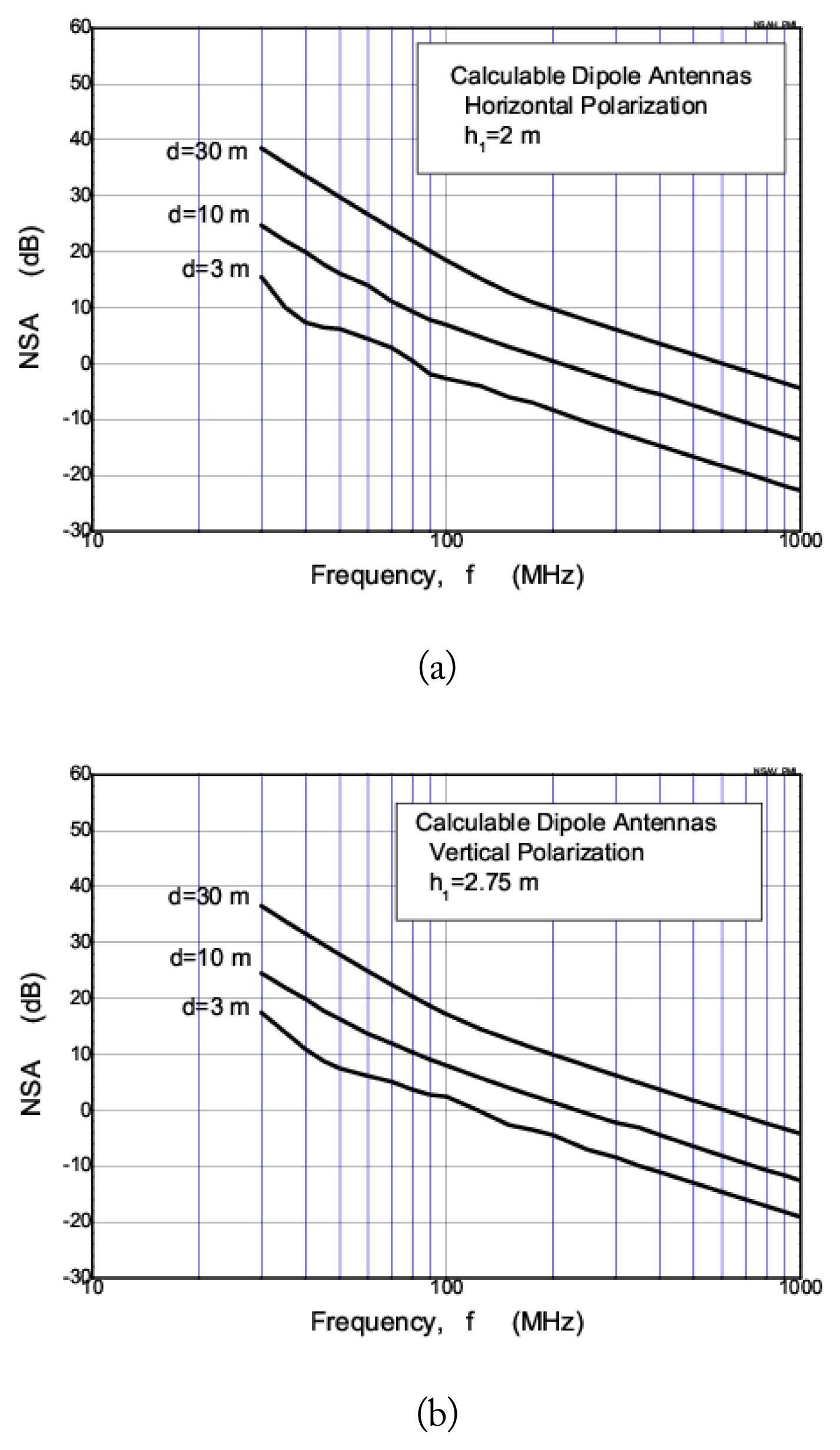
In the calculation of the theoretical NSA of an ideal OATS from Eqs. (3), (13), and (14), the TX and RX antenna system analysis is required, in which case a thin-wire kernel approximation with a segment length of 0.0125λ is used for the piecewise sinusoidal Galerkin’s methods of moment analysis, as presented in [19–21]. The dipole radius (α = 3.175 mm; 30 MHz ≤ f < 300 MHz and α = 0.794 mm; 300 MHz ≤ f ≤ 1 GHz ) was chosen to be less than 0.007λ (thin-wire approximation). A nominal value of 50 Ω was used for the characteristic impedance Z₀. A coaxial cable (RG-214/U) with a length of 10 m was selected for the numerical calculation (the velocity of propagation is 66% of the velocity in free space, and the dielectric constant ɛ_r is 2.3). Fig. 4 shows the frequency characteristics of the calculated theoretical NSA from Eq. (3) for the horizontal and vertical polarizations at given distances of 3 m, 10 m, and 30 m. The detailed values of the theoretical NSAs calculated in this paper are shown in Table 3. In these tables, the resonant dipole lengths for a CalDA with a 3-dB hybrid balun in the frequency range of 30 MHz to 1 GHz are shown for 24 individual frequencies. The height of the RX antenna when measuring the CSA at the given distances is also shown. These theoretical NSA values (Fig. 4, Table 3) were used as reference theoretical NSA values for the validation test of an OATS or a semi-anechoic chamber using the CalDAs.

Tables 4 and 5 show the AF₁, AF₂, and CSA values calculated from Eqs. (13) and (1). For example, a CSA of 13.34 dB is obtained when h₁ = 2 m and h₂ = 1.72 m with d = 3 m, H-polarization, and f = 100 MHz. In this case, TX and RX AFs are AF₁(2 m) = 8.15 dB(1/m) and AF₂(1.72 m) = 7.87 dB(1/m), respectively. From these CSAs, AF₁, and AF₂, the theoretical NSA from Eq. (4) is calculated as −2.68 dB. The resulting NSA values for 24 individual frequencies are shown in Fig. 4 and Table 3. Tables 4 and 5 are also useful for checking the AFs (AF₁ and AF₂) above the ground plane giving the NSA.

In general, AFs provided with the antenna are inadequate unless they are specifically or individually measured and the calibration is traceable to a national standard. In an actual validation test, the use of the AFs above the ground plane is inadequate because individual AF calibration at a given antenna height above the ground plane is needed, and this procedure is inefficient. For this reason, the FSAFs for the TX and RX antennas were used to determine the NSA measurements.

ANSI C63.5 gives the FSAFs for a tuned dipole with a Roberts balun. Tables 6 and 7 show the theoretical FSAFs for a CalDA. A comparison of both FSAFs, the Roberts dipole and the CalDA, is not adequate because the dipole radius, resonant lengths, and balun types are different. Nevertheless, the FSAF differences between both antennas are within 0.56 dB.

In a relevant standard, the theoretical NSA of an ideal OATS is developed and calculated using FSAFs and mutual impedance correction factors. ANSI C63.4 [1] provides theoretical NSA values and mutual impedance correction factors for the tuned dipoles with a Roberts balun and a 3-m site. When the theoretical NSA from FSAFs, NSA_FS, is used for the NSA measurement using the CalDA, the measured NSAs are different from the true NSA. Hence, ΔAF_TOT for the CalDA is necessary.

Tables 6 and 7 show the calculated NSA_FS from the FSAFs of the TX and RX antennas and the mutual impedance correction factors ΔAF_TOT for the CalDA. ΔAF_TOT is calculated from Eq. (16) and is known as the total AF difference, as explained in Section II-3. Hence, the FSAFs, AF_1FS and AF_2FS, are used to measure the NSA. Further, the mutual impedance correction factor, ΔAF_TOT, is provided to obtain the true NSA. For example, the NSA_FS of −3.06 dB is obtained from the CSA of 13.34 dB using the free space, AF_1FS, of 8.20 dB(1/m) at d = 3 m, H-polarization, and f = 100 MHz. In this case, the mutual impedance correction factor, ΔAF_TOT, is necessary, and from Table 6, since ΔAF_TOT = −0.38 dB, the desired NSA = −2.68 dB is obtained from Eq. (8). Tables 6 and 7 are useful for actual NSA measurement, using the FSAFs and the mutual impedance correction factors of the CalDA.

To validate a constructed site, the true theoretical NSA values are very important as a reference, and the measured NSA should be within ±4 dB. The use of AFs over the ground plane is inadequate because the AF calibration for an individual height over the ground plane is very hard and time consuming. Hence, the use of FSAFs is recommended for easy AF calibration and to save time. Consequently, we considered the true theoretical NSA of an ideal OATS, the FSAFs, and the AF correction factors (mutual impedance correction factors) for a CalDA and for 3-m, 10-m, and 30-m sites.

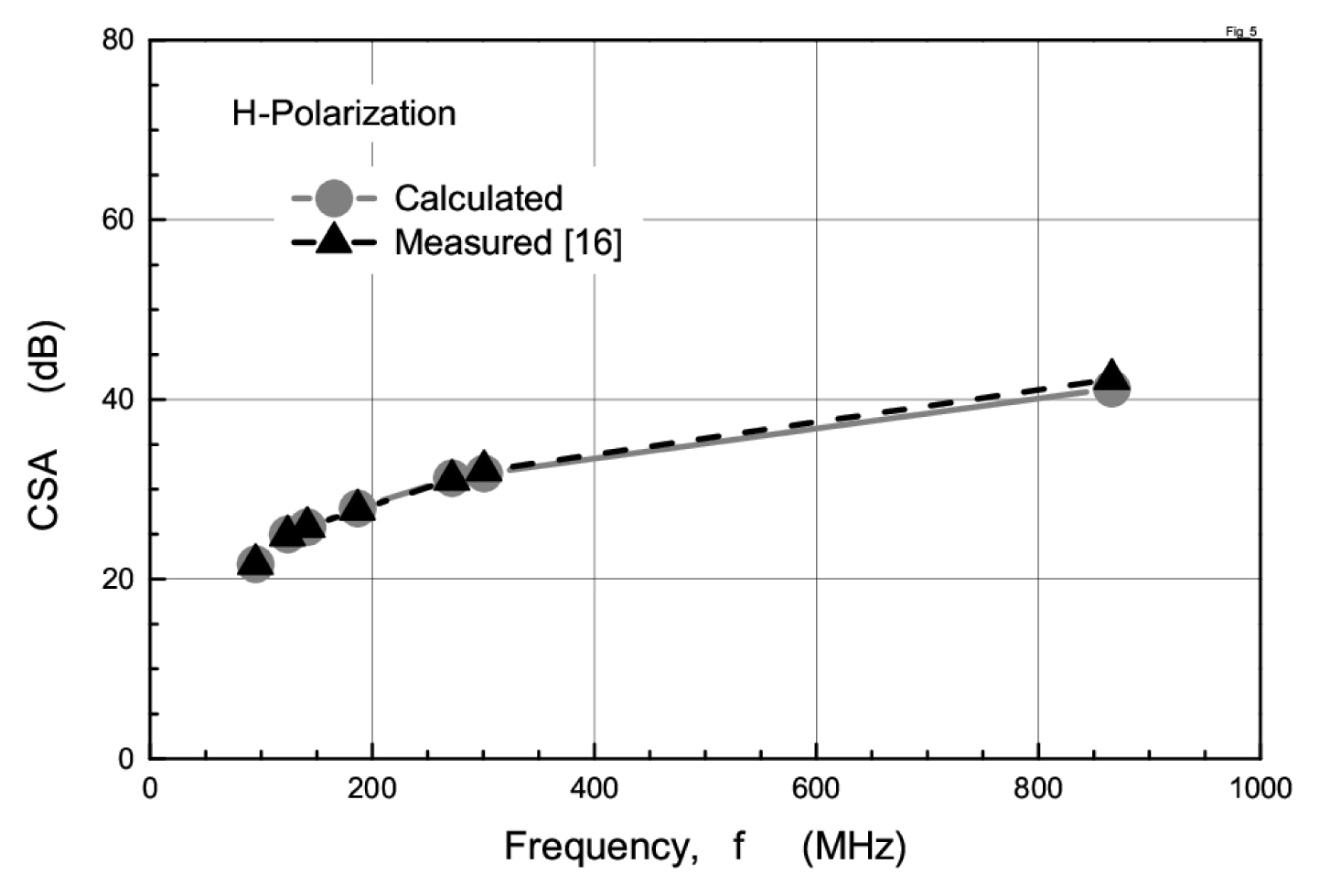
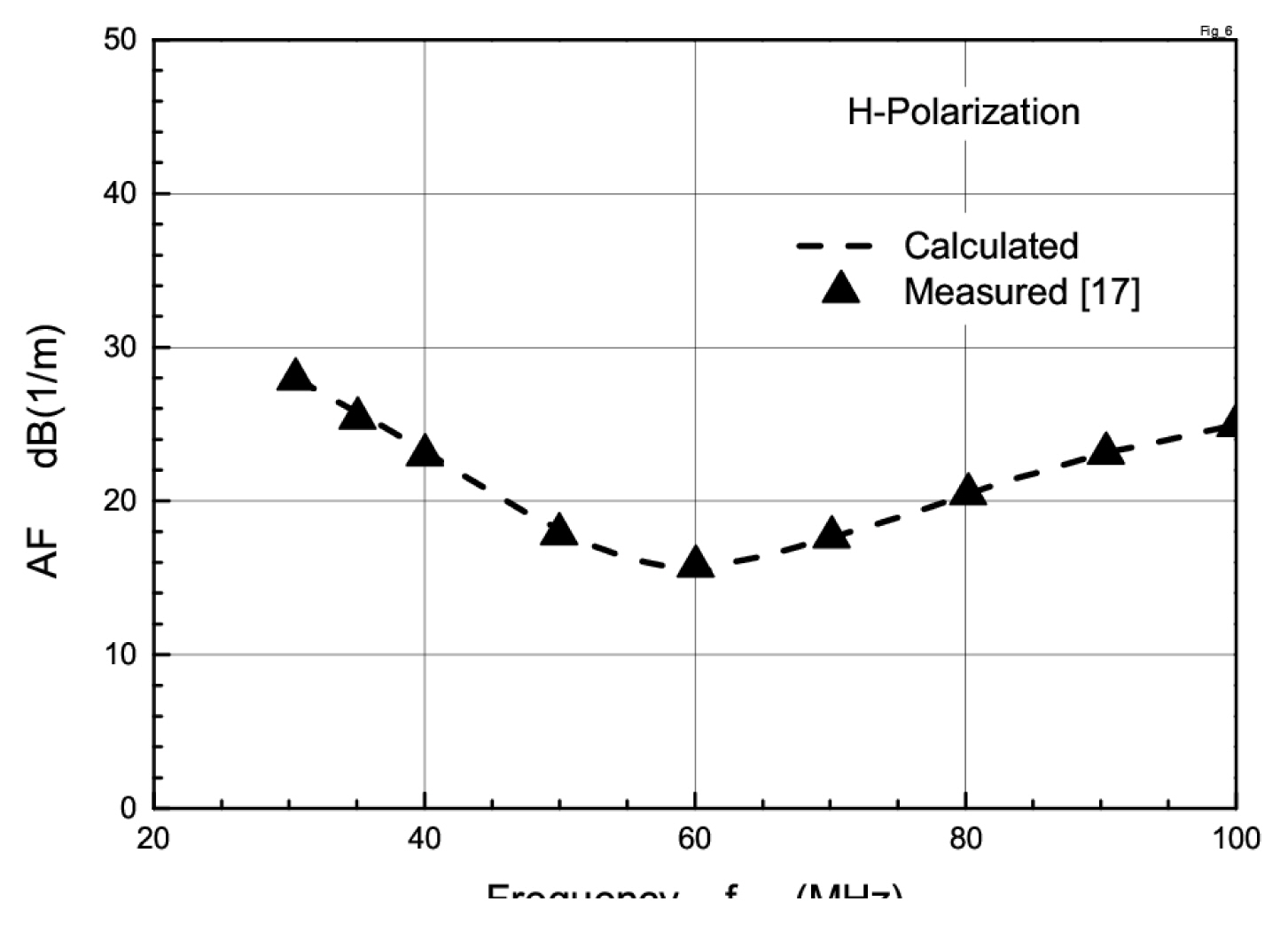
In order to calculate the NSA, the CSA and AFs are needed. To verify these theoretical analyses, the theoretical results of CSA and AF are compared with the experimental results [16, 17] in Figs. 5 and 6. The AF is measured by the two-antenna method. The results show that the calculated CSA and AF values are in good agreement with the measured results.