Efficient Finite-Difference Time-Domain Modeling of Time-Varying Dusty Plasma

Article information

J. Electromagn. Eng. Sci. 2022;22(4):1-7

Publication date (electronic) : 2022 July 31

doi : https://doi.org/10.26866/jees.2022.4.r.115

Yong-Jin Kim, Jeahoon Cho, Kyung-Young Jung

Department of Electronic Engineering, Hanyang University, Seoul, Korea

^*Corresponding Author: Kyung-Young Jung (e-mail: kyjung3@hanyang.ac.kr)

Received 2021 December 6; Revised 2021 December 27; Accepted 2022 February 2.

Abstract

The finite-difference time-domain (FDTD) method has been widely used for the electromagnetic analysis of dusty plasma sheath in reentering hypersonic vehicles. The time-varying characteristics of dusty plasma should be considered to accurately analyze THz wave propagation in dusty plasma. In this work, we propose an efficient FDTD modeling of time-varying dusty plasma based on the combination of the bilinear transform and the state-space approach. The proposed FDTD formulation for time-varying dusty plasma can lead to a significant improvement in computational efficiency against the conventional shift operator FDTD counterpart while maintaining numerical accuracy. Numerical examples are performed to validate the proposed FDTD modeling of time-varying dusty plasma.

Keywords: Dispersive Media; Electromagnetic Propagation in Plasma Media; Finite-Difference Time-Domain (FDTD) Method

I. Introduction

When hypersonic vehicles enter the atmosphere, the communication blackout problem occurs because of the dusty plasma sheath phenomenon [1]. Experimental research on electromagnetic (EM) wave propagation in dusty plasma is expensive and time consuming due to the high-temperature condition requirement. Alternatively, numerical research is promising to systematically analyze EM wave propagation in dusty plasma with various parameter conditions. The finite-difference time-domain (FDTD) method has been widely used to analyze EM wave interaction with complex media [2–6] due to its simplicity, robustness, and accuracy [7–11]. In a previous work [12], we proposed the FDTD formulation to be suitable for time-invariant dusty plasma by utilizing a bilinear transform (BT). For time-invariant dusty plasma, the BT-FDTD simulation was 2.64% faster than the conventional shift operator (SO)-FDTD formulation, with less memory requirements and the same numerical accuracy.

The electron density of dusty plasma changes with time [1, 13, 14]. Therefore, the time-varying characteristics of dusty plasma should be considered to accurately analyze EM wave propagation in dusty plasma. Note that time-varying coefficients should be updated every FDTD time marching in the FDTD formulations of time-varying media. In this work, we propose an efficient FDTD modeling suitable for time-varying dusty plasma. For this purpose, we first extend BT to the FDTD formulation of time-varying dusty plasma. A higher speedup of the BT-FDTD formulation versus the SO-FDTD formulation can be achieved for the time-varying dusty plasma than for the time-invariant case because fewer arithmetic operations are involved in updating time-varying coefficients in the BT-FDTD formulation. Moreover, the state-space approach is applied to the BT-and SO-FDTD formulations because it can reduce the memory requirement of dispersive FDTD formulations [15–17]. We apply the state-space approach to reduce the computation time and memory requirement in the BT-FDTD formulation for time-varying dusty plasma. Numerical examples illustrate that the proposed FDTD simulation is 118.63% faster than its SO-FDTD counterpart, albeit with the same computational accuracy and less memory usage.

II. FDTD Formulation for Time-Varying Dusty Plasma

In real dusty plasma, all parameters are time-invariant, except for electron density [13, 14]. The time-varying electron density N_e is defined as follows:

(1) Ne(t)=Ne,0 · f(t).

Here, f(t) represents the time-varying function, and N_e,0 is the constant of the electron density. The time-varying characteristic of electron density affects two dusty parameters. Therefore, angular plasma frequency ωpe2 (=Nee2/ɛ0me) and charging response factor ηed (=e2πrd2NeNd/me) should also be considered as time-varying characteristics as follows:

(2) ωpe2(t)=f(t) · ωpe,02

(3) ηed(t)=f(t) · ηed,0,

where ω_pe_,₀ and η_ed_,₀ are the constants of the angular plasma frequency and the charging response factor, respectively. In the equations above, ɛ₀ is the permittivity of free space, e is the electric charge of an electron, m_e is the mass of an electron, r_d is the radius of dust particles, and N_d is the density of dust particles. Note that other dusty parameters are time invariant.

In the following subsections, we first briefly discuss the conventional SO-FDTD formulation for time-varying dusty plasma and then address the extension of the state-space approach. We then propose an efficient BT-FDTD formulation with the state-space approach, which is highly suitable for time-varying dusty plasma, and present a comparison of computational efficiency for the SO- and BT-FDTD formulations.

1. SO-FDTD

The dispersion relative permittivity model of dusty plasma in the frequency domain can be expressed as [15]

(4) ɛr(ω)=ɛr,∞+(ωpe2νch-c0ηed/ɛ0)+ωpe2(jω)νeffνch(jω)+(νeff+νch)(jω)2+(jω)3,

where ɛ_r_,_∞ is relative permittivity at an infinite frequency, c₀ is the speed of light in free space, ν_ch is the dust charging frequency, and ν_eff is the effective collision frequency.

In the frequency domain, Maxwell’s curl equations and the constitutive equation can be written as follows:

(5) ∇×E(ω)=-jωμ0H(ω)

(6) ∇×H(ω)=jωD(ω)

(7) D(ω)=ɛ0ɛr(ω)E(ω).

The time-domain governing equations are obtained by applying the inverse Fourier transform. The update equations for SO-FDTD can be derived by applying the central difference scheme (CDS) to the resulting Maxwell’s curl equations and the SO approach to the time-domain constitutive equation.

(8) Hn+1/2=Hn-1/2-Δtμ0∇×En

(9) Dn+1=Dn+Δt∇×Hn+1/2

(10) En+1=1ɛ0 · Ba(t){AaDn+1+AbDn+AcDn-1+AdDn-2}-1Ba(t){Bb(t)En+Bc(t)En-1+Bd(t)En-2}

where

Aa=q0+q1 (2Δt)+q2 (2Δt)2+q3 (2Δt)3Ab=3q0+q1 (2Δt)-q2 (2Δt)2-3q3 (2Δt)3Ac=3q0-q1 (2Δt)-q2 (2Δt)2+3q3 (2Δt)3Ad=q0-q1 (2Δt)+q2 (2Δt)2-q3 (2Δt)3Ba(t)=p0(t)+p1(t) (2Δt)+p2 (2Δt)2+p3 (2Δt)3Bb(t)=3p0(t)+p1(t) (2Δt)-p2 (2Δt)2-3p3 (2Δt)3Bc(t)=3p0(t)-p1(t) (2Δt)-p2 (2Δt)2+3p3 (2Δt)3Bd(t)=p0(t)-p1(t) (2Δt)+p2 (2Δt)2-p3 (2Δt)3

with

p0(t)=ωpe2(t)νch-c0ηed(t)/ɛ0,q0=0p1(t)=ɛr,∞νeffνch+ωpe2(t),q1=νeffνchp2=ɛr,∞(νeff+νch),q2=νeff+νchp3=ɛr,∞,q3=1.

Here, the superscript indicates the FDTD time index, and Δt represents the FDTD time step size. The update coefficients B_a–B_d are the functions of time, and they can be rewritten by decomposing the time-varying and the time-invariant parts. For example, B_a is expressed as

Ba(t)=f(t) · Ba,0+Ba,cBa,0=ωpe,02νch-c0ηed,0/ɛ0+ωpe,02 (2Δt)Ba,c=ɛr,∞νeffνch (2Δt)+p2 (2Δt)2+p3 (2Δt)3.

In actual FDTD simulations, the update coefficients are usually pre-calculated before the FDTD time marching to speed up the computation time. However, for the FDTD formulation of time-varying dusty plasma, the time-varying coefficients should be updated for each FDTD time loop. In Eq. (10), many field components on the right-hand side are included, which leads to a large memory requirement.

In this work, the state-space approach [16–18] is employed to reduce memory usage. In the state-space approach, field variables at the same time step are assigned to a new alternative variable. For example, the update equation for E in Eq. (10) can be written as

(11) En+1=1Ba,0 · f(t)+Ba,c(AaDn+1/ɛ0+W1n)W1n+1=AbDn+1ɛ0-(Bb,0 · f(t)+Bb,cEn+1)+W2nW2n+1=AcDn+1ɛ0-(Bc,0 · f(t)+Bc,cEn+1)+W3nW3n+1=AdDn+1ɛ0-(Bd,0 · f(t)+Bd,cEn+1).

The variable W₁ represents the grouped field variables at the time step n in Eq. (10), and W₂ and W₃ represent the variables at n–1 and n–2, respectively. Note that five field components are required in the SO-FDTD method with the state-space technique, while seven field components are needed in the standard SO-FDTD method.

2. BT-FDTD

Here, we discuss an efficient FDTD modeling for the EM analysis of time-varying dusty plasma. In our previous work [12], the computational efficiency of the BT-FDTD formulation was better than that of the SO-FDTD formulation for the EM analysis of time-invariant dusty plasma. In the current work, we propose the FDTD modeling to be highly suitable for time-varying dusty plasma by utilizing both the BT and the state-space approach.

In BT-FDTD, Ampere’s equation and the constitutive equation in the frequency domain are expressed as follows:

(12) ∇×H(ω)=jωɛ0ɛr(ω)E(ω)=jωɛ0ɛr,∞E(ω)+J(ω)

(13) J(ω)=jωχ(ω)E(ω)

with

χ(ω)=(ωpe2νch-c0ηed/ɛ0)+ωpe2(jω)νeffνch(jω)+(νeff+νch)(jω)2+(jω)3.

The FDTD update equation of E can be obtained by applying the inverse Fourier transform to Eq. (12) and then the CDS to the resulting equation:

(14) En+1=En-Δtɛ∞(∇×Hn+12+Jn+1+Jn2),

where ɛ_∞=ɛ₀ɛ_r_,_∞. The FDTD update for J is derived by utilizing the BT approach to Eq. (13):

(15) Jn+1=CbaJn+CbbJn-1+Cbc(t)En+1+Cbd(t)En+Cbe(t)En-1.

Note that in the BT approach, jω is approximated as

(16) jω≅2Δt1-z-11+z-1.

In the above equations, the coefficients are as follows:

Cba=8b2-2b0Δt2b0Δt2+2b1Δt+4b2Cbb=-b0Δt2+2b1Δt-4b2b0Δt2+2b1Δt+4b2Cbc(t)=f(t) · ɛ0a0,0Δt2+2ɛ0a1,0Δtb0Δt2+2b1Δt+4b2Cbd(t)=f(t) · 2ɛ0a0,0Δt2b0Δt2+2b1Δt+4b2Cbe(t)=f(t) · ɛ0a0,0Δt2-2ɛ0a1,0Δtb0Δt2+2b1Δt+4b2

with

a0,0=ωpe,02νch-c0ηed,0/ɛ0a1,0=ωpe,02b0=νeffνchb1=νeffνchb2=1.

It is worth noting that only multiplication is involved in the time-varying coefficients, unlike in the SO-FDTD formulation, in which addition and multiplication are required. The FDTD update equation for H is the same as that for SO-FDTD. As the Eⁿ⁺¹ field in Eq. (14) cannot be updated explicitly, we plug Eq. (15) into Eq. (14).

The resulting FDTD update equation for E is expressed as follows:

(17) En+1=11+f(t) · Cbe,02Δtɛ∞{(1-f(t) · Cbd,0Δt2ɛ∞) En-(f(t) · Cbe,0Δt2ɛ∞) En-1-Δtɛ∞(∇×Hn+12)-(cbaΔt+Δt2ɛ∞) Jn-cbbΔt2ɛ∞Jn-1}.

Three coefficients are functions of time in the proposed BT-FDTD formulation, while four coefficients are time varying in the SO-FDTD formulation.

We then apply the state-space approach to the BT-FDTD method. The FDTD update equation for J can be expressed as follows:

(18) Jn+1=f(t) · Cbc,0En+1+W1n

(19) W1n+1=CbaJn+1+f(t) · Cbd,0En+1+W2n

(20) W2n+1=CbbJn+1+f(t) · Cbe,0En+1

Comparing the above update equation with Eq. (15), one field variable is less required by applying the state-space technique.

Note that unlike SO-FDTD, BT-FDTD can further simplify the E field update equation by using the state-space approach. In Eq. (17), we can replace the variables at time step n–1 in W2n+1 [see Eq. (20)] as

(21) En+1=11+f(t) · Cbe,02Δtɛ∞[En-Δt2ɛ∞{f(t) · Cbd,0En+2 · ∇×Hn+12+(Cba+1)Jn+W2n-1}].

By using Eq. (19), we can simplify the above equation as follows:

(22) En+1=(11+f(t) · Cbe,02Δtɛ∞)×{En-Δt2ɛ∞(2 · ∇×Hn+12+Jn+W1n)}.

In this additional manipulation, the complexity of the E field update equation of BT-FDTD is drastically reduced, enhancing the computational efficiency of BT-FDTD.

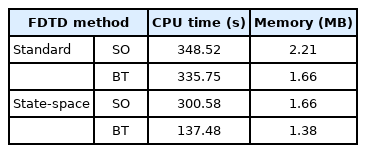
Table 1 shows the memory requirement and the number of arithmetic operations of the SO-FDTD and BT-FDTD formulations for time-varying dusty plasma. Here, A/S indicates addition/subtraction, and M/D indicates multiplication/division. Note that the arithmetic operations for the time-varying update coefficients are included in this table. In the table, we consider the standard FDTD method (without the state-space approach) and the FDTD method with the state-space approach. The memory requirement for the BT-FDTD formulation is less than that for the SO-FDTD formulation, regardless of whether the state-space approach is applied. In addition, the BT-FDTD formulation with the state-space approach is significantly better than the SO-FDTD formulation in terms of computation time (related to the number of arithmetic operations). It should be noted that in the EM analysis of time-varying dusty plasma, the state-space technique is more appropriate for the BT-FDTD formulation than for the SO-FDTD formulation with respect to computation time because it can be efficiently used in two FDTD update equations of the former formulation but only in one update equation of the latter. Table 2 presents the details of the computational efficiency of the FDTD formulations with the state-space approach. Additional operations are required for time-varying characteristics. More A/S operations are not required in the BT-FDTD formulation compared to SO-FDTD, thus implying better computational efficiency of the former than the latter.

Table 1

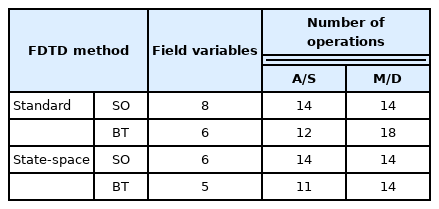
Computational efficiency of FDTD formulations for time-varying dusty plasma (per one-dimensional computational unit cell)

Table 2

Details of the computational efficiency of the state-space FDTD update equations (per one-dimensional computational unit cell)

III. Numerical Examples

We investigate the computational efficiency and accuracy of the SO-FDTD and BT-FDTD formulations. We use one-dimensional inhomogeneous dusty plasma with a thickness of 0.15 m and 30 slabs with different N_e, following [14]. The other dusty plasma parameters are N_d = 10¹² m³, ν_eff = 10 GHz, and ν_ch = 8.7 GHz. The simulation frequency range is 1–100 GHz. We define the FDTD space step size as Δz = 40 μm and the FDTD time step size as Δt =0.125 ps. The computational domain is terminated by 10-cell perfectly matched layers [19–21]. All FDTD simulations are performed using an Intel i7-10700 CPU.

Time-invariant dusty plasma is analyzed by setting f(t) to validate our FDTD simulations. As shown in Figs. 1 and 2, both FDTD simulations agree well with [22]. We then simulate the FDTD formulations with the state-space approach for time-varying dusty plasma. In this work, two time-varying functions are considered: f1(t)=t/Tr for 0<t<T_r [1] and f₂(t)=t/T_r for 0 < t < T_r [14]. In both cases, T_r (=8000Δt) is the time limit when dusty plasma becomes stable and the time-varying function becomes one after T_r. As shown in Figs. 1 and 2, the BT-FDTD simulations are in good agreement with the SO-FDTD simulations, regardless of the time-varying characteristic and the state-space approach. The reflection coefficients decrease because of the time-varying functions in the entire frequency range (Fig. 1). Conversely, the transmission coefficients increase for time-varying dusty plasma compared to time-invariant dusty plasma (Fig. 2).

Fig. 1

Reflection coefficient of SO-FDTD and BT-FDTD for dusty plasma. The black line denotes the theoretical result for time-invariant dusty plasma.

Fig. 2

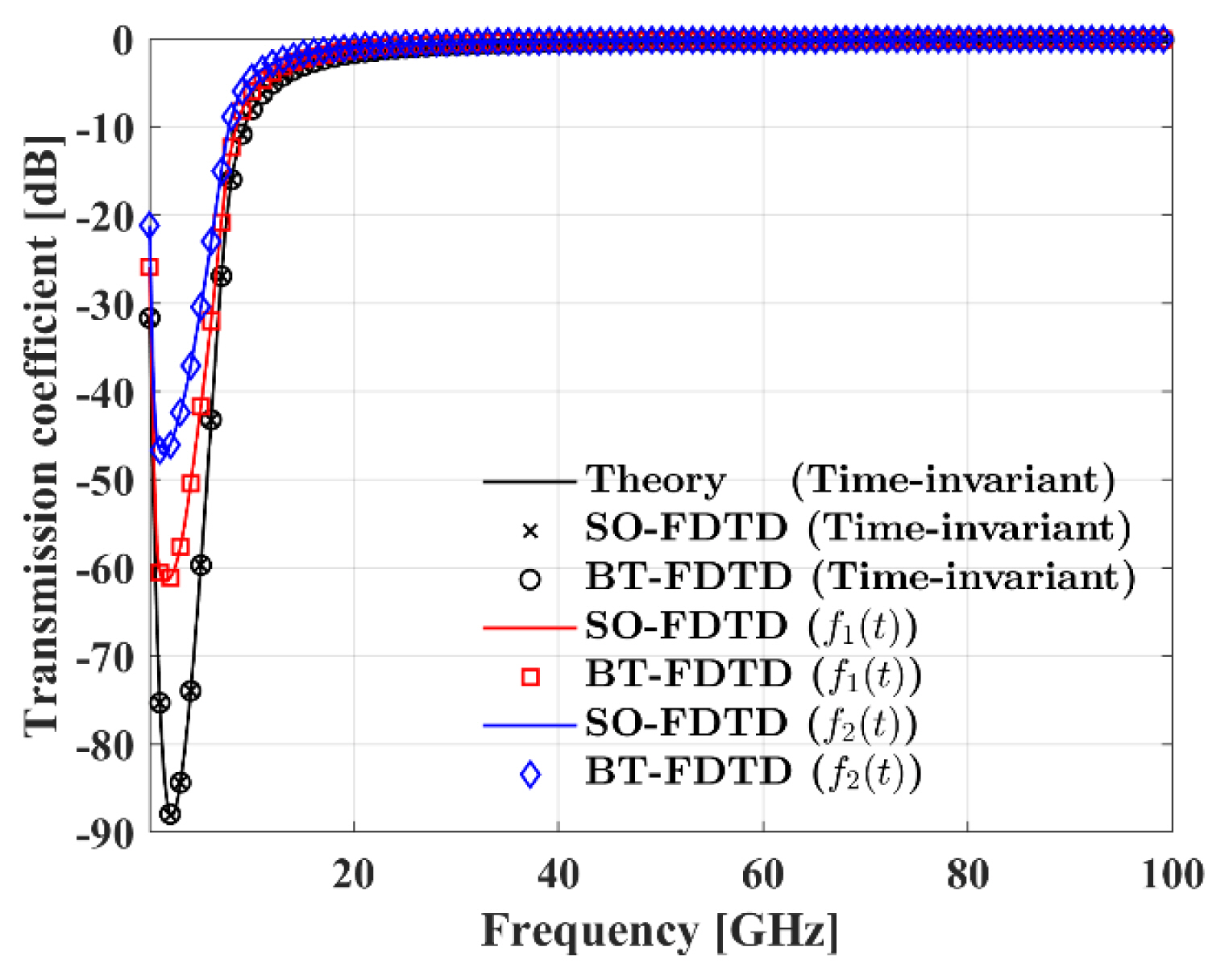
Transmission coefficient of SO-FDTD and BT-FDTD for dusty plasma. The black line denotes the theoretical result for time-invariant dusty plasma.

We then compare the computation time and memory cost of FDTD simulations (with and without the state-space approach) for time-varying dusty plasma. As shown in Table 3, the computational efficiency of the BT-FDTD formulation is better than that of the SO-FDTD formulation. For the standard FDTD method (without the state-space approach), the BT-FDTD simulation is 3.7% faster than the SO-FDTD simulation. However, the BT-FDTD formulation with the state-space approach is approximately 118.63% faster than the SO-FDTD formulation. For time-invariant dust plasma, the BT-FDTD simulation is 2.64% faster than the SO-FDTD simulation [12]. Moreover, less memory cost is required for the BT-FDTD simulations than for the SO-FDTD simulations.

Table 3

Computational efficiency of FDTD simulations for time-varying dusty plasma

IV. Conclusion

In this work, we propose an efficient FDTD formulation for EM wave propagation in time-varying dusty plasma using the BT technique and the state-space approach. BT-FDTD is more adaptable to time-varying dusty plasma than SO-FDTD. Moreover, the state-space approach is more effective for the proposed BT-FDTD formulation than for the SO-FDTD formulation in the EM analysis of time-varying dusty plasma. We apply the state-space approach to the J field update equation of BT-FDTD by grouping the variables at the same time step as the W variables. We optimize the E field update equation of BT-FDTD using the defined W variables. As a result, the FDTD update formulation of BT-FDTD is much simpler than that of SO-FDTD and has better computational efficiency in time and memory, with the same accuracy. Numerical examples are used to validate the computational efficiency improvement in the proposed FDTD modeling of time-varying dusty plasma. The proposed FDTD modeling approach using the combination of BT and the state-space approach can be extended to other time-varying dispersive media in nanophotonics and metamaterials.

Acknowledgments

This work was supported by the Laboratory of Computational Electromagnetics for Large-scale Stealth platform (No. UD200047JD).

References

1. Wang M., Yu M., Xu Z., Li G., Jiang B., Xu J.. Propagation properties of terahertz waves in a time-varying dusty plasma slab using FDTD. IEEE Transactions on Plasma Science 43(12)4182–4186. 2015.

2. Alsharahi G., Faize A., Maftei C., Bayjja M., Louzazni M., Driouach A., Khamlichi A.. Analysis and modeling of GPR signals to detect cavities: case studies in Morocco. Journal of Electromagnetic Engineering and Science 19(3)177–187. 2019.

3. Choi H., Kim Y. H., Baek J. W., Jung K. Y.. Accurate and efficient finite-difference time-domain simulation compared with CCPR model for complex dispersive media. IEEE Access 7160498–160505. 2019.

4. Choi H., Baek J. W., Jung K. Y.. Comprehensive study on numerical aspects of modified Lorentz model-based dispersive FDTD formulations. IEEE Transactions on Antennas and Propagation 67(12)7643–7648. 2019.

5. Smy T. J., Stewart S. A., Rahmeier J. G., Gupta S.. FDTD simulation of dispersive metasurfaces with Lorentzian surface susceptibilities. IEEE Access 883027–83040. 2020.

6. Choi H., Baek J. W., Jung K. Y.. Numerical stability and accuracy of CCPR-FDTD for dispersive media. IEEE Transactions on Antennas and Propagation 68(11)7717–7720. 2020.

7. Taflove A., Hagness S. C.. Computational Electrodynamics: The Finite-Difference Time-Domain Method 3rd edth ed. Norwood, MA: Artech House; 2005.

8. Gedney S. D.. Introduction to the Finite-Difference Time-Domain (FDTD) Method for Electromagnetics Lexington, KY: Morgan & Claypool; 2010.

9. Ha S. G., Cho J., Choi J., Kim H., Jung K. Y.. FDTD dispersive modeling of human tissues based on quadratic complex rational function. IEEE Transactions on Antennas and Propagation 61(2)996–999. 2013.

10. Hyun S. Y.. Improved discrete-time boundary condition for the thin-wire FDTD analysis of lossy insulated cylindrical antennas located in lossy media. Journal of Electromagnetic Engineering and Science 21(1)60–63. 2021.

11. Park J., Jung K. Y.. Numerical stability of modified Lorentz FDTD unified from various dispersion models. Optics Express 29(14)21639–21654. 2021.

12. Kim Y. J., Jung K. Y.. Accurate and efficient finite-difference time-domain formulation of dusty plasma. IEEE Transactions on Antennas and Propagation 69(10)6600–6606. 2021.

13. Yang M., Li X. P., Liu Y. M., Shi L., Xie K.. Propagation of electromagnetic signals in the time-varying plasma. Acta Physica Sinica 63(8)article no. 085201. 2014. https://doi.org/10.7498/aps.63.085201 .

14. Wei C., Yang L., Huang Z., Guo L.. Research on the propagation characteristics of THz waves in spatial inhomogeneous and time-varying and weakly ionized dusty plasma. IEEE Transactions on Plasma Science 47(10)4745–4752. 2019.

15. Shukla P. K., Mamun A. A.. Introduction to Dusty Plasma Physics London, UK: Taylor & Francis; 2001. p. 36–69.

16. Kuo B. C.. Automatic Control Systems Englewood Cliffs, NJ: Prentice-Hall; 1975.

17. Ha S. G., Cho J., Kim E. K., Park Y. B., Jung K. Y.. FDTD dispersive modeling with high-order rational constitutive parameters. IEEE Transactions on Antennas and Propagation 63(9)4233–4238. 2015.

18. Park S. M., Kim E. K., Park Y. B., Ju S., Jung K. Y.. Parallel dispersive FDTD method based on the quadratic complex rational function. IEEE Antennas and Wireless Propagation Letters 15425–428. 2016.

19. Teixeira F. L., Chew W. C.. A general approach to extend Berenger’s absorbing boundary condition to anisotropic and dispersive media. IEEE Transactions on Antennas and Propagation 46(9)1386–1387. 1998.

20. Cho J., Park M. S., Jung K. Y.. Perfectly matched layer for accurate FDTD for anisotropic magnetized plasma. Journal of Electromagnetic Engineering and Science 20(4)277–284. 2020.

21. Jang S., Jung K. Y.. Perfectly matched layer formulation of the INBC-FDTD algorithm for electromagnetic analysis of thin film materials. IEEE Access 9118099–118106. 2021.

22. Balanis C. A.. Advanced Engineering Electromagnetics 2nd edth ed. Hoboken, NJ: Wiley; 2012.

Biography

Yong-Jin Kim received his B.S. degree from the Department of Electronic Engineering at Hanyang University, Seoul, Republic of Korea, in 2019. He is currently working toward his Ph.D. degree in the Department of Electronic Engineering at the same university. His current research interest is computational electromagnetics.

Jeahoon Cho received his B.S. degree in communication engineering from Daejin University, Pocheon, Republic of Korea, and his M.S. and Ph.D. degrees in electronics and computer engineering from Hanyang University, Seoul, Republic of Korea, in 2004, 2006, and 2015, respectively. From 2015 to August 2016, he was a postdoctoral researcher at Hanyang University. Since September 2016, he has worked at Hanyang University, where he is currently a research professor. His current research interests include computational electromagnetics and EMP/EMI/EMC analysis.

Kyung-Young Jung received his B.S. and M.S. degrees in electrical engineering from Hanyang University, Seoul, Republic of Korea, in 1996 and 1998, respectively, and his Ph.D. degree in electrical and computer engineering from Ohio State University, Columbus, USA, in 2008. From 2008 to 2009, he was a postdoctoral researcher at Ohio State University, and from 2009 to 2010, he was an assistant professor in the Department of Electrical and Computer Engineering, Ajou University, Suwon, Republic of Korea. Since 2011, he has worked at Hanyang University, where he is now a professor in the Department of Electronic Engineering. His current research interests include computational electromagnetics, bioelectro-magnetics, and nanoelectromagnetics. Dr. Jung was a recipient of the Graduate Study Abroad Scholarship from the National Research Foundation of Korea, the Presidential Fellowship from Ohio State University, the HYU Distinguished Teaching Professor Award from Hanyang University, and the Outstanding Research Award from the Korean Institute of Electromagnetic Engineering and Science.

Article information Continued

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Update field	BT-FDTD			SO-FDTD

	E	J	H	E	D	H
Field array	Eⁿ	Eⁿ*	Eⁿ*	Eⁿ	Dⁿ*	Eⁿ*
	Jⁿ	Jⁿ*	Hn+12*	Dⁿ	Hn+12	Hn+12*
	W1n	W1n*		W1n
	Hn+12	W2n		W2n
				W3n
A/S	4	5	2	6	2	2
A/S⁺	0	0	0	4	0	0
M/D	4	5	1	8	1	1
M/D⁺	1	3	0	4	0	0

FDTD method		CPU time (s)	Memory (MB)
Standard	SO	348.52	2.21
	BT	335.75	1.66
State-space	SO	300.58	1.66
	BT	137.48	1.38