A Compact Low-Loss Reflection-Type Harmonic Transponder for Battery-Less RFID Sensors Based on Harmonic Backscattering

Daju Lee; Juntaek Oh

doi:10.26866/jees.2023.5.r.182

Abstract

This study presents a compact reflection-type harmonic transponder with a wide input power range for battery-less radio-frequency identification (RFID) sensors based on harmonic backscattering. Miniaturizing the circuit size of conventional harmonic transponders is difficult because the input and output matching stages are configured separately, and two antennas are used for each port. The proposed harmonic transponder based on a dual-band matching network matches the load simultaneously at the fundamental and second harmonic frequencies over a wide input power range, thus enhancing the conversion gain (CG) with a compact size. For verification, the proposed transponder is implemented in a compact size with dimensions of 19 mm × 17.8 mm. The measured CG of the implemented transponder is maintained at over −10 dB in the wide input power range of −6.4 to 10.6 dBm at 2.45 GHz. The harmonic transponder is configured with a dual-band chip antenna and measured in free space to verify whether it is suitable for battery-less RFID sensors. The measured detectable effective distance to the proposed circuit is 6.3 m in free space, with an equivalent isotropically radiated power of 42.6 dBm.

Keywords: Backscattering, Dual-Band Matching Network (DBMN), Harmonic Transponder, Nonlinear Radar, RFID Sensors

I. Introduction

Recently, Internet of Things (IoT) technology, which connects all objects to the internet and controls various information from objects, has progressed with 5G technology, which enables high-speed internet connectivity. As the number of various IoT devices is increasing rapidly, the use of technology to classify and track various IoT devices has become more important. A radiofrequency identification (RFID) tag can be a simple solution in IoT technology to help identify and locate objects without batteries in a way that reflects a transmitted signal with its information [1]. However, it is vulnerable to interference and noise from the surrounding environment because of the received weak signal reflected by an RFID tag with a relatively small scattering cross-section [2].

A harmonic transponding-based RFID tag, which receives fundamental waves and reflects harmonics generated by nonlinear electronic elements, including diodes, transistors, and field-effect transistors (FETs), is an alternative approach to enhancing the signal-to-noise ratio [3]. The harmonic transponder comprises a diode and an input and output matching network. The configuration method of the harmonic transponder is classified into a reflection type, whose input and output terminals are combined [4, 5], and a through type, whose input and output terminals are separated [3, 6–10]. By implementing each matching network, the through-type harmonic transponder can easily match the input impedance to the source at the fundamental frequency, and the output impedance to the load at the harmonic frequency. However, it is unsuitable for compact RFID tags because it may require two antennas and both input and output matching networks. In [11], a diplexer-based harmonic transponder can provide high isolation between Tx and Rx antennas, even with only one antenna. However, in addition to requiring an additional diplexer design, the bandwidth of the harmonic transponder can be narrowed by the diplexer.

In this study, we propose a reflection-type harmonic transponder for battery-less RFID sensors. The proposed circuit comprises a dual-band matching network (DBMN) and a diode for harmonic backscattering. It is possible to implement a harmonic transponder with low insertion loss and a small size with only the DBMN to match the load at the fundamental and harmonic frequencies simultaneously. The proposed circuit is implemented in an ultra-small size of 19 mm × 17.8 mm. As a result of the measurement, a conversion gain (CG) of over −10 dB is maintained in the input power range of −6.4 to 10.6 dBm at 2.45 GHz. The proposed harmonic transponding-based RFID tag with a chip antenna can be detected from a distance of 6.3 m with a transmitted equivalent isotropic radiated power (EIRP) of 42.6 dBm.

II. Harmonic Transponder Design

As one of the methods to configure the harmonic transponder, the number of elements, including antennas and matching networks, in the reflection-type harmonic transponder can be decreased; however, but the DBMN is required to have a high second harmonic exciting response of the harmonic transponder with low insertion loss [12, 13]. In this design, we introduce a low-loss reflection-type harmonic transponder with a transmission-line based DBMN, as shown in Fig. 1. A transmission line-based matching network has a large impedance change according to frequency and can accurately predict the input impedance of the matching network using electromagnetic (EM) simulation compared to a lumped element-based matching network with a tolerance of about 5%–10% [14]. Thus, it is suitable for composing a network that matches the load at the desired fundamental and harmonic frequencies.

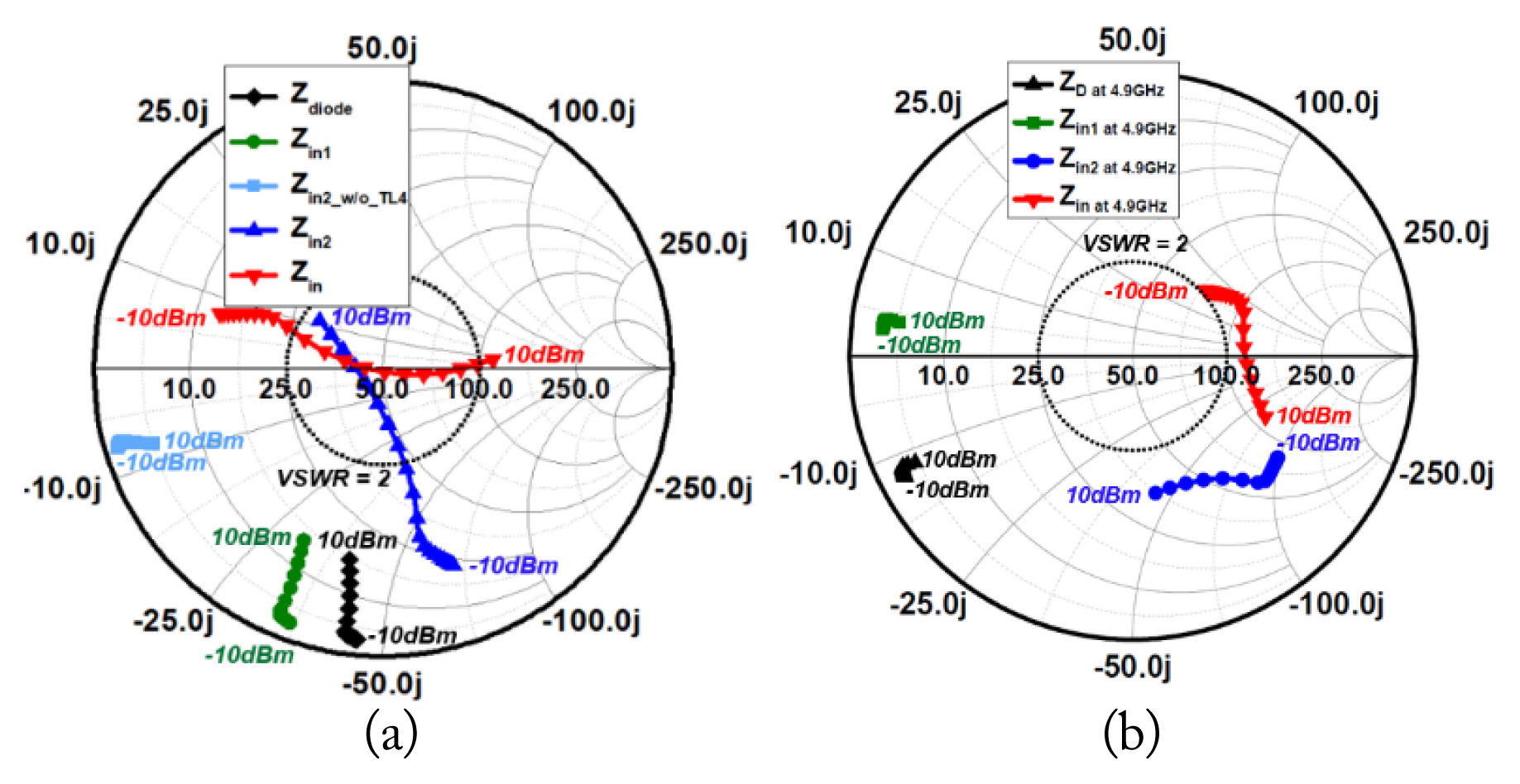
Fig. 2 shows the simulated input and output impedance of the proposed harmonic transponder with different input power levels at the target fundamental frequency of 2.45 GHz and the second harmonic frequency of 4.9 GHz. A series transmission line, TL₅, is the interconnection line between a harmonic generating diode and the DBMN. A shorted stub TL₄ parallel to the diode acts as both a DC feed (0 V) and the matching network at the fundamental frequency without affecting the input impedance at the second harmonic frequencies, as the electrical length of TL₄ is set to λ/4 at 4.9 GHz. As depicted in Fig. 2(a) and 2(b), the width of TL₄ and the length and width of an open stub TL₃ are optimized to shift the input impedance Z_D close to the voltage standing wave ratio (VSWR) = 2 circle at 2.45 GHz and 4.9 GHz. Series transmission lines TL₁ and TL₂ are set to change the input impedance Z_in at 4.9 GHz adjacent to the VSWR = 2 circle, whereas Z_in at 2.45 GHz remains almost unchanged.

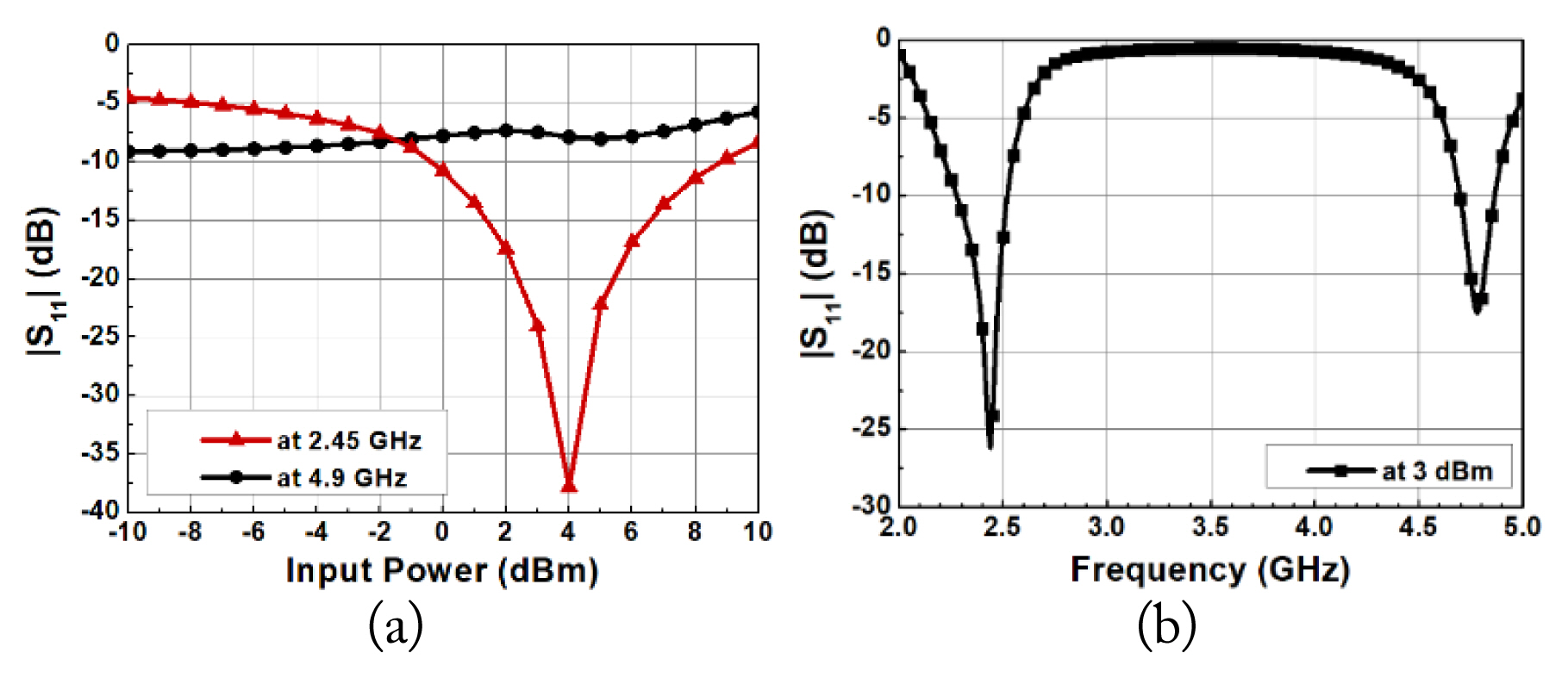
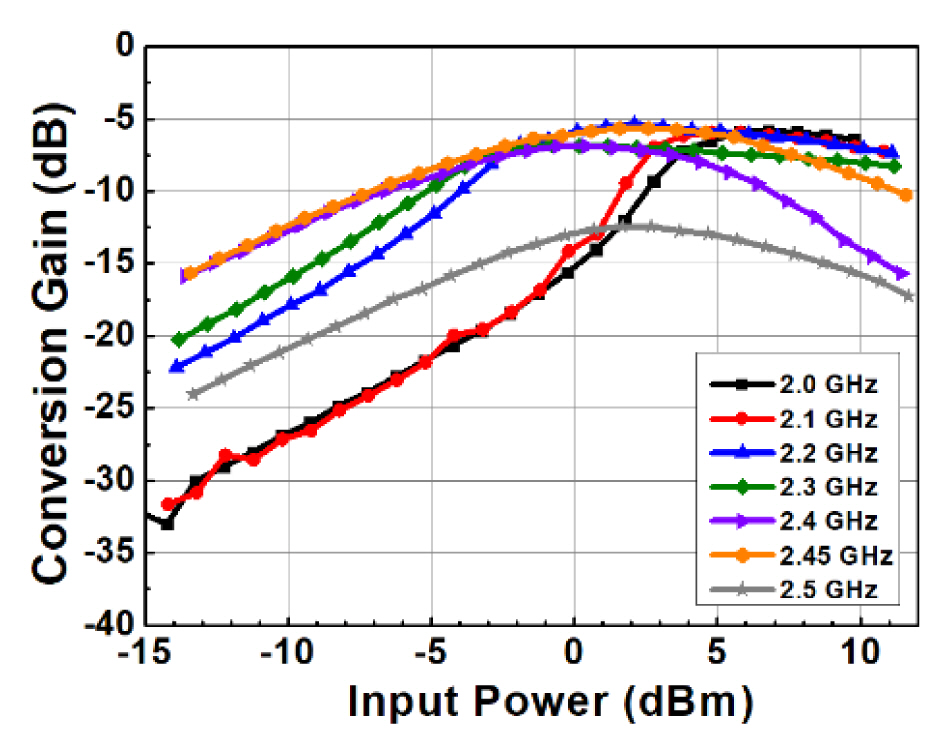
Fig. 3(a) presents the simulated input return loss |S₁₁| of the proposed harmonic transponder at 2.45 GHz and GHz with different input power levels. |S₁₁| is under −10 dB in the input power range of −0.3 to 8.8 dBm at 2.45 GHz and under −5 dB in the input power range of −10 to 10 dBm at 4.9 GHz. As shown in Fig. 3(b), |S₁₁| is under −10 dB in the fundamental and second harmonic bands of 2.28–2.52 GHz and 4.7–4.86 GHz. The simulated CG of the proposed harmonic transponder with different frequencies and input power levels is obtained, as shown in Fig. 4. The proposed circuit obtains a high CG of over −10 dB in the wide input power range of −4 to 7 dBm when the operating frequency varies from 2.25 GHz to 2.5 GHz, as the diode of the harmonic transponder matches the load well at the fundamental and second harmonic frequencies within a wide input power range.

III. Implementation and Experimental Evaluation

As illustrated in Fig. 5, the proposed harmonic transponder was fabricated using Taconic’s TLC-32 substrate (dielectric constant = 3.2, loss tangent = 0.003, thickness = 0.813 mm). The Skyworks SMV-1430-040LF diode varactor was used as a nonlinear element. The input and output DC blocking capacitors were adopted at 12 pF. The circuit was optimized via harmonic balance, a large signal S-parameter, and an EM simulator based on the Advanced Design System. To verify the implemented harmonic responder, a second harmonic output power and a CG were measured using a Keysight E8247C signal generator and a Keysight E4407B spectrum analyzer. As shown in Fig. 6, the proposed harmonic transponder achieved a peak CG of −6.5 dB and maintained a CG of above −10 dB in the wide input power range of −6.4 to 10.6 dBm at 2.45 GHz. Fig. 7 shows the measured CG with frequency and input power. It remained above −10 dB in the 2.2–2.45 GHz frequency band, as the input power level varied from −3.9 to 6.4 dBm. The peak CG from −5.3 to −7.5 dB was obtained in the frequency range of 2.0–2.45 GHz at an input power of 3.1 dBm.

To check whether the proposed harmonic transponder is detectable from a long distance, the circuit consisted of a W3006 chip antenna (Pulse Electronics, San Diego, CA, USA), and the measurement environment was set up in a radio anechoic chamber, as shown in Fig. 8(a) [15]. The W3006 chip antenna had a gain of 2.0 dBi at 2.45 GHz, and the extrapolated gain value at 4.9 GHz was about 3.0 dBi. The fundamental signal was produced by a Keysight E8247C signal generator, an OPHIR5183 power amplifier (Test Equipment Connection Corp., Lake Mary, FL, USA), and an LFCN-3400 low-pass filter (Mini-Circuits, Brooklyn, NY, USA). A BBHA-9120-LF horn antenna (Schwarzbeck, Schonau, Germany), as a transmit antenna, was connected to the low-pass filter. The second harmonic signal was received using a Keysight E4407B spectrum analyzer with a VT58SGAH20NK horn antenna (Vector Telecom, Melbourne, Australia). In the measurement setup, the distance between the target and the Tx and Rx antennas was 2.3 m.

Fig. 8(b) shows the calculated and measured second harmonic signals of the proposed harmonic transponder and various electronic devices. The output power received was calculated using the Friis transmission equation in [11]. The second harmonic power received from the harmonic transponder was at least 23.7 dB greater than that from the electronic devices at 49.6 dBm of the EIRP. The difference between the calculation and measurement results was caused by the difference in CG according to the input power and the inaccuracy of the antenna model.

As illustrated in Fig. 9(a), the harmonic transponder was also measured with the same equipment in the building corridor to obtain the maximum detectable distance. Fig. 9(b) shows the measured harmonic response of the proposed harmonic transponder at 42.6 dBm of the EIRP. The maximum detectable range was 6.3 m because of the limited corridor length. The difference between the calculation and measurement results was due to the reflection signals from the wall and the ground.

Table 1 presents the performance comparisons of the proposed harmonic transponder to previous works. It shows that the proposed circuit has one of the highest CGs and the widest dynamic input power range and the smallest size.

IV. Conclusion

This study presented a novel harmonic transponder and verified the feasibility of the proposed circuit as an RFID sensor. The reflection-type harmonic transponder that can be shared between the input and output terminals considered a DBMN to reduce the insertion loss in the wide input power range, minimizing the circuit size. The proposed harmonic transponder achieved a high CG of over −10 dB in the input power range of 6.4–10.6 dBm at 2.45 GHz and in the frequency range of 2–3 GHz at an input power of 13 dBm. The maximum detectable range of the proposed harmonic transponding-based RFID tag consisted of a 6.3 m chip antenna when the transmitted EIRP of the signal generator with a horn antenna was 42.6 dBm.

Acknowledgments

This work was supported by the Soongsil University Research Fund (New Professor Support Research) of 2020. The EDA tool was supported by the IC Design Education Center (IDEC), Korea.

Fig. 1

Schematic of the proposed harmonic transponder.

Fig. 2

Simulated input and output impedance of the proposed harmonic transponder with different input power levels: (a) input impedance at 2.45 GHz and (b) output impedance at 4.9 GHz.

Fig. 3

Simulated return loss |S₁₁| (a) at 2.45 GHz and 4.9 GHz with different input power levels and (b) with different frequencies at 3 dBm of input power.

Fig. 4

Simulated conversion gain (CG) of the proposed harmonic transponder with frequency and input power.

Fig. 5

Layout and photograph of the proposed harmonic transponder.

Fig. 6

Simulated and measured conversion gain versus input power at 2.45 GHz.

Fig. 7

Measured conversion gain with input power and frequency.

Fig. 8

Measurement in the radio anechoic chamber: (a) the measurement setup and (b) the measured received power of the proposed harmonic transponder.

Fig. 9

The measurement in the building corridor: (a) the measurement setup and (b) the measured received power of the proposed harmonic transponder.

Table 1

Comparison of the recently reported harmonic transponder

	Polivka et al. [4]	Palazzi et al. [6]	Raju and Bridges [7]	Gu et al. [11]	This work
Frequency (GHz)	0.894	2.08	2.5	3.5	2.45
Peak CG
CG (dB)	−5a	−15.1	−11.5	−20.2	−6.5
P_in (dBm)	−20a	−10	5b	−30	−1.5
Power range for CG > −10 dB (dB)	13.5b	N/A	N/A	N/A	17.3
Frequency BW for the peak CG > −10 dB (GHz)	N/A	N/A	N/A	N/A	2.0–2.45
Type	Reflection	Reflection	Through	Through	Reflection
Size (λ²)	0.32 × 0.16	0.28 × 0.28	0.1 × 0.16	0.25 × 0.25	0.16 × 0.15

^a Graphically estimated,

^b power range for conversion gain (CG) > −25 dB.

References

1. S. Mondal and P. Chahal, "A passive harmonic RFID tag and interrogator development," IEEE Journal of Radio Frequency Identification, vol. 3, no. 2, pp. 98–107, 2019. https://doi.org/10.1109/JRFID.2019.2910234

2. D. W. Steele, F. S. Rotondo, and J. L. Houck, "Radar system for manmade device detection and discrimination from clutter," U.S. Patent No, 7830299. Nov 9 2010.

3. T. M. Silveira, P. Pinho, and N. B. Carvalho, "Harmonic RFID temperature sensor design for harsh environments," IEEE Microwave and Wireless Components Letters, vol. 32, no. 10, pp. 1239–1242, 2022. https://doi.org/10.1109/LMWC.2022.3172027

4. M. Polivka, V. Hubata-Vacek, and M. Svanda, "Harmonic balance/full-wave analysis of wearable harmonic transponder for IoT applications," IEEE Transactions on Antennas and Propagation, vol. 70, no. 2, pp. 977–987, 2022. https://doi.org/10.1109/TAP.2021.3111226

5. F. Amato and S. Hemour, "The harmonic tunneling tag: a dual-band approach to backscattering communications," In: Proceedings of 2019 IEEE International Conference on RFID Technology and Applications (RFID-TA); Pisa, Italy. 2019, pp 244–247. https://doi.org/10.1109/RFID-TA.2019.8891996

6. V. Palazzi, L. Roselli, M. M. Tentzeris, P. Mezzanotte, and F. Alimenti, "Energy-efficient harmonic transponder based on on-off keying modulation for both identification and sensing," Sensors, vol. 22, no. 2, article no. 620, 2022. https://doi.org/10.3390/s22020620

7. R. Raju and G. E. Bridges, "A compact wireless passive harmonic sensor for packaged food quality monitoring," IEEE Transactions on Microwave Theory and Techniques, vol. 70, no. 4, pp. 2389–2397, 2022. https://doi.org/10.1109/TMTT.2022.3142063

8. A. Lavrenko, B. Litchfield, G. Woodward, and S. Pawson, "Design and evaluation of a compact harmonic transponder for insect tracking," IEEE Microwave and Wireless Components Letters, vol. 30, no. 4, pp. 445–448, 2020. https://doi.org/10.1109/LMWC.2020.2972744

9. L. Zhu, T. D. Ha, Y. H. Chen, H. Huang, and P. Y. Chen, "A passive smart face mask for wireless cough monitoring: a harmonic detection scheme with clutter rejection," IEEE Transactions on Biomedical Circuits and Systems, vol. 16, no. 1, pp. 129–137, 2022. https://doi.org/10.1109/TBCAS.2022.3148725

10. X. Hui, T. B. Conroy, and E. C. Kan, "Near-field coherent sensing of vibration with harmonic analysis and balance signal injection," IEEE Transactions on Microwave Theory and Techniques, vol. 69, no. 3, pp. 1906–1916, 2021. https://doi.org/10.1109/TMTT.2021.3053978

11. X. Gu, N. N. Srinaga, L. Guo, S. Hemour, and K. Wu, "Diplexer-based fully passive harmonic transponder for sub-6-GHz 5G-compatible IoT applications," IEEE Transactions on Microwave Theory and Techniques, vol. 67, no. 5, pp. 1675–1687, 2019. https://doi.org/10.1109/TMTT.2018.2883979

12. K. Rasilainen, J. Ilvonen, J. M. Hannula, and V. Viikari, "Designing harmonic transponders using lumped-component matching circuits," IEEE Antennas and Wireless Propagation Letters, vol. 16, pp. 246–249, 2016. https://doi.org/10.1109/LAWP.2016.2570938

13. A. Lehtovuori, R. Valkonen, and M. Valtonen, "Dual-band matching of arbitrary loads," Microwave and Optical Technology Letters, vol. 56, no. 12, pp. 2958–2966, 2014. https://doi.org/10.1002/mop.28747

14. J. Kim, S. K. Hong, and J. Oh, "Highly efficient power amplifier based on harmonic-controlled matching network," IEEE Microwave and Wireless Technology Letters, vol. 33, no. 1, pp. 43–46, 2023. https://doi.org/10.1109/LMWC.2022.3196669

15. S. Y. Oh, K. H. Cha, H. Hong, H. Park, and S. K. Hong, "Measurement of nonlinear RCS of electronic targets for nonlinear detection," Journal of Electromagnetic Engineering and Science, vol. 22, no. 4, pp. 447–451, 2022. https://doi.org/10.26866/jees.2022.4.r.108

Biography

Daju Lee received her B.S. degree from the Department of Robotics Engineering, Yeungnam University, Gyeongsan, Korea, in 2021. She is currently pursuing her integrated M.S. and Ph.D. degrees in electronic engineering at Soongsil University, Seoul, South Korea. Her research interests include wireless power transfer technology and radar systems.

Biography

Juntaek Oh received his B.S., M.S., and Ph.D degrees in electronics and electrical engineering from Korea Advanced Institute of Science and Technology, Daejeon, Korea, in 2010, 2012, and 2016, respectively. From 2016 to 2018, he worked with the Advanced Medical Device Research Division at Korea Electrotechnology Research Institute in Ansan, Korea. From 2018 to 2020, he was an assistant professor in the Department of Robotics Engineering at Yeungnam University in Gyeongsan, Korea. Since 2020, he has been with the School of Electronic Engineering at Soongsil University, where he is currently an associate professor. His main research interests are analog/RF/mmW CMOS ICs and radar systems.