An Investigation of Harmonic Oscillation of an Ion Particle in a Non-uniform Electrostatic Field

Jatupon Em-Udom; Nattapon Jaisumroum

doi:10.26866/jees.2023.5.r.186

J. Electromagn. Eng. Sci > Volume 23(5); 2023 > Article

Em-Udom and Jaisumroum: An Investigation of Harmonic Oscillation of an Ion Particle in a Non-uniform Electrostatic Field

Regular Paper

Journal of Electromagnetic Engineering and Science 2023;23(5):390-397.

Published online: September 30, 2023

DOI: https://doi.org/10.26866/jees.2023.5.r.186

An Investigation of Harmonic Oscillation of an Ion Particle in a Non-uniform Electrostatic Field

Jatupon Em-Udom¹, Nattapon Jaisumroum^2,^*

¹National Security and Dual-Use Technology Center, National Science and Technology Development Agency, Pathumthani, Thailand

²Department of Sustainable Development Technology, Faculty of Science and Technology, Thammasat University, Pathumthani, Thailand

^*Corresponding Author: Nattapon Jaisumroum (e-mail: nattaponj@tu.ac.th)

Received October 6, 2022 Revised December 7, 2022 Accepted January 19, 2023

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this study, we investigate the possibility to trap an ion particle in a non-uniform electrostatic field generated by two ionic rings, with the aim to obtain and verify general results regarding our proposition. To develop the equation of motion, we first derive the electric field generated by each ring, based on the multipole expansion technique under the azimuthally symmetrical charge distribution speculation and superposition principle. Then, we establish the equation of motion regarding the Lagrangian formalism. From the results, we observe that an ion particle can exhibit harmonic motion, if the stability condition is satisfied by an appropriate parametric setting. The results are confirmed by displacement responses and phase trajectory plots, which validate our belief in the prospect to trap an ion in an electrostatic field. Furthermore, the velocity amplitude is significantly influenced by both the charge concentration of each ring and its size.

Keywords: Electrostatic Force, Harmonic Oscillation, Ionic Ring, Non-uniform Electrostatic Field, Trapped Ion Particle

I. Introduction

Trapped ion technology has become one of the most exciting fields recent years as it results in a number of cutting-edge research areas and technologies, for example, fundamental physics experiments to investigate atomic or molecular properties [1, 2], chemical mass analyzer mass spectrometry to determine, with high precision, the molecular weights of complex compounds [3–5], and a building block of isolated ion to serve as a qubit in trapped ion quantum computer technology [6–9]. These inventions and technologies introduce a number of emerging industrial sectors that accelerate and deliver enormous impacts on communities worldwide.

Samuel Earnshaw first investigated the stability issue to control a charged particle in free space in an electrostatic field [10]. His study has laid the foundation and paved the direction for current ion trap techniques. So far, there have been two most common types, namely Paul trap and Penning trap techniques. The former technique [11–13] was first introduced by Paul [14]; it employs dynamic electric fields to trap a charged particle by creating an average confining force in all three directions that change over time. The latter technique [15, 16] was proposed by Han Georg Dehmelt, inspired by Penning’s vacuum gauge invention. It is noteworthy that this specific schematic differs from the Paul trap technique by adopting an electrostatic field, instead of a time-varying electric field, accompanied by a uniform magnetic field to confine an ion particle.

Despite some researches dedicated to studying several applications employing Paul and Penning trap techniques [17–20], the works that have investigated, in rigorous detail, the possibility to confine an ion particle in a non-uniform electrostatic field remain limited. Still skeptical, we believe that there should be a prospect to confine an ion particle in free space using an electrostatic field [21, 22], but its spatial distribution should be under non-uniform conditions. Therefore, in this study, our objective is to attempt to prove and affirm that idea through in silico investigation, based on the developed mathematical model of the equation of motion of an ion particle in a non-uniform electrostatic field induced by two ionic rings with a common centerline. A one-dimensional model is employed in this work to conveniently obtain and readily verify our proposition. To develop the equation of motion, we first establish the electrostatic field model generated by each ring using the multipole-expansion technique under the azimuthally symmetrical charge distribution assumption [23–25], rather than using a boundary condition approach found in Jackson’s study [26]. Then, we apply the superposition principle to determine the total electrostatic field generated by both rings, and the equation of motion is finally obtained based on the Lagrangian mechanics’ framework [27, 28]. It is important to note that the total electrostatic field is expressed in the quadratic potential function, of which Legendre polynomials [29] in the series expansion are addressed up to order n = 2, where the higher-order terms after n = 3 are truncated due to the small amplitude of oscillation assumption.

II. Electrostatic Theory

1. Method for an Electrostatic Potential Function

To find an electrostatic potential function generated by an azimuthally symmetrical charge distribution in a free region, as shown in Fig. 1(a), the multipole expansion method [23–25] is employed to determine the form of electrostatic. We recall the potential charge distribution in integral form as Eq. (1):

(1)

ϕ(r,θ)=14πɛ0∫v′ρ(r′,θ′)‖r-r′‖dV′,

where ϕ(r, θ) denotes the electrostatic potential function created by the volumetric charge density distribution function ρ(r′, θ′), r and θ respectively signify a radial distance and an inclination angle in the polar spherical coordinate at the location under consideration, while r′ and θ′, respectively represent a radial distance and an inclination angle in the polar spherical coordinate (pointing to the location of a charge distribution), and dv′ denotes the infinitesimal volumetric body of a charge distribution. To express 1/||r-r′|| in the algebraic form to facilitate the upcoming derivation process the definition of the vector norm is employed.

(2)

1‖r-r′‖=1r2+r′2-2r·r′.

Next, we specify that r > represents the maximum magnitude between ||r|| and ||r′||, whereas r < denotes the minimum magnitude between these two variables, namely r > = max (||r||,||r′||) and r < = min (||r||,||r′||). Therefore, Eq. (2) can be rewritten, as shown in Eq. (3):

(3)

1‖r-r′‖=11+(r</r>)2-(2r·r′)/(r>)2.

Obviously, r < is less than r >; in other words, r < / r > is literally less than unity; r </r > < 1, which leads to (r < / r >)² – 2(r. r′)/(r >)² and is also less than unity, according to the binomial series expansion definition, can be rewritten, as shown in Eq. (4):

(4)

1‖r-r′‖=1r>[1+r·r′r>2+3(r·r2)-(r<r>)22r>4+5(r·r′)3-3(r·r′)(r<r>)22r>6+…].

It is important to note that if the r < r′ condition is satisfied, the potential field relation provided by Eq. (4) is finally obtained under an azimuthally symmetrical charge distribution speculation [23–25]. This can be expressed by an integral form, as shown in Eq. (5):

(5)

ϕ(r,θ)=14πɛ0Σn=0∞rn pn(cosθ)∫v′ρ(r′,θ′)(r′)n+1pn(cosθ′)dV′.

Note that ϕ(r, θ) represents the electrostatic potential generated by a distributed charge at r and θ coordinate, p_n(cosθ) is a Legendre polynomial of order n as a function of cos θ parameter, ρ(r′, θ′) denotes a density function of azimuthally symmetrical charge distribution r′and θ′coordinate, p_n(cosθ′) is a Legendre polynomial of order n [29] corresponding to cosθ′parameter, and v′ signifies the volume of an azimuthally symmetrical charge distribution. The numerical orders of the Legendre polynomial function are provided in Table 1.

2. Determination of Electrostatic Potential Function

In this section, we demonstrate how the electric potential function of a single ionic ring, illustrated in Fig. 2, is developed using Eq. (5).

According to the system configuration, the ionic ring center is located above the origin in the z-axis direction, where the position under consideration at radial distance r is confined within the c value to ascertain that the r < r′ condition has been met. The azimuthally symmetrical charge distribution density function of a single ionic ring, per Fig. 2 in the polar spherical coordinate adapted from Hassani [34] and Wang [35], is given via Eq. (6) below,

(6)

ρ(r′,θ′)=Kcδ(r′-c)δ(cosθ′-cosα),

where K is a constant that we need to determine, and δ(u) represents a Dirac-delta function [29, 34, 35]. To find K, we integrate Eq. (6) over an ionic ring body to ensure that its integral value is equal to total charge Q via Eq. (7):

(7)

Q=∫02π∫0π∫0aKcδ(r′-c)δ(cosθ′-cosα)dV′=∫02π∫-11∫0aKcδ(r′-c)δ(cosθ′-cosα)r′2dr′dcosθ′d∅′=Kc∫02πd∅′∫-11δ(cosθ′-cosα)dcosθ′∫0cr′2 δ(r′-c)dr′)=K2πc,

where K=Q2πc. Therefore, the electric potential function using Eq. (5) can be rewritten, as shown in Eq. (8):

(8)

ϕring(r,θ)=Q8π2ɛ0c2Σn=0∞rnPn(cosθ)∫02πd∅′∫-11Pn (cosθ′)δ(cosθ′-cosα)dcosθ′∫0cδ′(r-c)r′n-1dr′,

where ϕ_ring(r, θ) represents the electrostatic potential of the ionic ring shown in Fig. 2 at r, θ coordinate, Q denotes the total charge of an ionic ring under the uniform charge distribution assumption, and ɛ₀ signifies the vacuum electric permittivity parameter, which can be rewritten, as shown in Eq. (9):

(9)

ϕring(r,θ)=Q4πɛ0Σn=0∞rncn+1Pn(cosα)Pn (cosθ).

It is noteworthy that Eq. (9) is legitimate if the position under consideration is not greater than the c value, r < c, as shown in Fig. 2, which enables us to conveniently analyze and study the electrostatic potential field near the origin’s location. In the next section, we develop a one-dimensional equation of motion for a trapped ion confined in a non-uniform electrostatic field generated by two ionic rings, based on Eq. (9), to investigate how a trapped ion behaves in this field when restricted to one dimension.

III. Motion of a Trapped Ion in a Non-uniform Electrostatic Field

In this section, our objective is to develop the equation of motion of a trapped ion in a non-uniform electrostatic field generated by two ionic rings, based on Eq. (9), from the simplest perspective, a one-dimensional study. This equation of motion provides us with an opportunity to more conveniently investigate the behavior of a trapped ion in an electrostatic field generated by two rings. To achieve this objective, first, we must determine the electrostatic field generated by two rings with a common centerline, as shown in Fig. 3(a). Although the centerlines of both rings have a common axis, the axis of ionic ring 1 points to the z¹ direction, whereas that of ring 2 points to the z² direction, as shown in Fig. 3(b). Nonetheless, the electrostatic field generated by each ring is still based on Eq. (9), with a different parameter setting. The electrostatic functional form of each ionic ring can be provided using Eq. (10):

(10)

ϕringi(z,θi)=Q4πɛ0Σn=0∞zn(l2)2+a2n+1Pn(cosα)Pn (cosθi),

where ϕringi(z,θi) and θⁱ represent the electrostatic field function and the inclination angle of the ring, respectively. According to Fig. 3(b), θ¹ = 0 and θ² = π if the positive sign pointing to the z¹ direction is specified.

(11)

ϕring1(z,0)=Q4πɛ0Σn=0∞zn(l2)2+a2n+1Pn{l2(l2)2+a2}Pn(1).

The electrostatic potential for ring 2 can be provided using Eq. (12):

(12)

ϕring2(z,π)=Q4πɛ0Σn=0∞zn(l2)2+a2n+1Pn{l2(l2)2+a2}Pn(-1).

To determine the total electrostatic potential generated by both ionic rings, we use the superposition principle to determine its functional form, ϕringtot(z):

(13)

ϕringtot(z)=Q4πɛ0Σn=0∞zn(l2)2+a2n+1Pn{l2(l2)2+a2}{Pn(1)+Pn(-1)}.

If we neglect higher-order expansion terms due to the small motion speculation in the vicinity of the origin point and focus only on n = 0, 1, 2 orders, where all expansion terms after n = 3 are not considered, Eq. (13) becomes Eq. (14):

(14)

Φringtot(z)≈Q4πɛ0{2((l2)2+a2)1/2+2(l2)2-a2((l2)2+a)5/2}·z2

Where Φringtot(z) represents the approximated quadratic electrostatic potential function generated by two common centerline ionic rings, per Fig. 3, where the higher-order expansion terms after n = 2 are truncated. It is important to note that P₀(x) = 1, P₂(x) = (3x² – 1)/2 per Table 1, and P₁(1) + P₁(1) = 0 condition have been employed to obtain Eq. (14), based on Eq. (13). To develop the equation of motion of an ion particle in the z direction in the non-uniform electrostatic field using Eq. (13), we assume the idea of a hypothetical tube, an imaginary tube shown in Fig. 3(a), to limit the motion of an ion particle in one dimension and implement the Lagrangian definition [27, 28], where L(z,z˙)=T(z˙)-Φringtot(z), to derive a one-dimensional equation of motion based on Lagrangian mechanics, as defined in Eq. (15):

(15)

ddt(∂L∂z˙)=(∂L∂z),T(z˙)=12mz˙2.

Based on Eq. (14), we can derive the equation of motion of a charged particle in the z direction, per Lagrangian mechanics, as shown in Eq. (15). Therefore, the equation of motion of this charged particle in a non-uniform electrostatic field generated by two ionic rings becomes Eq. (16):

(16)

mz¨+{qQ4πɛ0·(l2)-2a2((l2)2+a2)5/2}z=0,

where ɛ₀ = 8.854 × 10^–12 F/m, the electric permittivity in a vacuum in the SI unit, and q = 1.6 × 10⁻¹⁹ C, the electrical charge of an ion in the SI unit. Eq. (16) represents the linear second-order differential equation that can exhibit a harmonic motion if appropriate parameters have been set up to ensure that the stability condition has been satisfied, that is, l > 2a. If the stability condition is met, the time interval of harmonic motion based on Eq. (16) is provided using Eq. (17):

(17)

T=16π3mɛ0qQ(l2-2a2){(l2)2+a2}5/4.

IV. Methodology

We divide our investigation into two parts. In the first part, we aim to demonstrate that a trapped ion can be confined and can exhibit harmonic motion in one dimension in a nonuniform electrostatic field generated by two ionic rings. We use the numerical solver, ode45 MATLAB function, to solve Eq. (16), to show that the periodic motion of a trapped ion is observed, where initial displacement z(0) = 0.018 m, and initial velocity ż (0) = 0 m/s are used to run our simulation. We specifically examine how the magnitude of the electrical charge of each ring, represented by ζ = Q/q parameter, significantly influences ion particle displacement responses. Additionally, the effect of an ion ring size, represented by ring radius a, on the time interval of the oscillation has been thoroughly studied. All parameters used to run the simulation in this part are provided in Table 2. In the second part of our investigation, we focus on studying the impact of ζ = Q/q parameter, the magnitude of the electrical charge of each ring, on velocity response, as well as how its maximum velocity amplitudes are influenced by the ring size, represented by ring radius a. All parameter settings in this part are also listed in Table 2.

V. Results and Discussion

1. Displacement Responses and Time Interval

In the first part, we have attempted to verify that a trapped ion in a non-uniform electrostatic field generated by two ionic rings with a common centerline, as illustrated in Fig. 3 is able to exhibit the harmonic motion calculated using Eq. (16). Thus, to conduct numerical studies in this part, all parameters have been set up per the information provided in Table 2, and the numerical results are illustrated in Fig. 4. According to the simulation results shown in Fig. 4(a), we notice that a trapped ion can exhibit oscillatory motion in a non-uniform electrostatic field generated by two ionic rings, as expected, because the motion of a trapped ion is apparently able to demonstrate periodic motion patterns between two rings for every testing parameter condition, where ζ = 1, 5, and 10. To verify the stability of these periodic motions, we establish the phase trajectory plots, as illustrated in Fig. 5, where all setting parameters are provided in Table 2, to ascertain whether the system has stable periodic motions. Based on the phase portrait, we discover that all phase trajectories, ζ = 1, 5, and 10, exhibit an elliptical motion around the equilibrium position at the point of origin without asymptotically stable and unstable evidence, indicating that all trajectories respond in a neutrally stable manner. These simulation results confirm the prospect of confining an ion particle in a non-uniform electrostatic field generated by two ionic rings, based on a one-dimensional speculation.

We also observe that the time interval of oscillation, T, highly depends on the magnitude of the electrical charge, represented by ζ parameter. In Fig. 4(a), it is noticeable that the time interval of oscillation of an ion particle tends to decrease when the ζ parameter value increases, indicating that the system will oscillate at a higher frequency rate if the electrical charge in each ring has greater concentration. We investigate this observation in detail to determine how significantly the electrical charge concentration in an ionic ring influences the time interval of oscillation, per Fig. 4(b), where ζ parameter ranges from 1 to 10. As a result, we observe that the time interval of oscillation, T, is remarkably influenced by ζ parameter, the magnitude of electrical charge in each ring. Specifically, the time interval of oscillation decreases when ζ parameter tends to increase, as expected, which confirms our belief that a trapped ion will respond at a higher frequency at an elevated electrical charge concentration. Lastly, we also find that the time interval of oscillation is considerably dependent on the ring size, represented by ring radius a—that is, an ion particle oscillates at a higher frequency and a shorter time interval when the ring size becomes smaller, as shown in Fig. 4(b).

2. Velocity Responses based on Changes in Charge Ratio

In this part, we investigate how the velocity responses of an ion particle in a non-uniform electrostatic field generated by two ionic rings (Fig. 3) differ if ζ parameter, the magnitude of the electrical charge of each ionic ring, has been altered, per the data provided in Table 2. The simulation results discussed in this part are shown in Fig. 6. In Fig. 6(a), we observe that the velocity responses of a trapped ion highly depend on ζ parameter, where ζ = 1, 5, and 10 are used in our study, per the information in Table 2. Regarding the simulation results, it is quite clear that not only does ζ parameter affect the time interval of oscillation of a trapped ion, as discussed earlier, but also has a considerable effect on the amplitude of velocity responses—that is, the amplitude will significantly rise if the magnitude of the electrical charge in each ring becomes higher. To validate the observation in detail, it can be confirmed through another numerical experiment, as shown in Fig. 6(b), where the velocity amplitude of ion oscillation noticeably increases when ζ parameter rises, based on the latter value ranging from 1 to 10. This indicates that an ion particle in a non-uniform electrostatic field is likely to oscillate at a higher velocity when the magnitude of the electrical charge in each ring becomes more concentrated. Another interesting observation is the effect of the ring size, represented by ring radius a, on the velocity amplitude of oscillation, which tends to increase if ring radius a becomes smaller, as illustrated in Fig. 6(b).

VI. Conclusion

In this work, we investigate and analyze the possibility to trap an ion particle in a non-uniform electrostatic field produced by two ionic rings with a common centerline. In our study, a trapped ion is limited to moving in a one-dimensional direction by introducing the hypothetical tube (imaginary tube) to assume that the motion of an ion particle within the tube moves in a one-dimensional direction. To develop the equation of motion of an ion particle, we first derive the electrostatic field generated by two ionic rings by employing the multipole expansion technique under the azimuthally symmetrical charge distribution assumption, where the higher-order expansion terms of Legendre polynomials after order n = 3 are negligible due to the small amplitude oscillation speculation. Then, the equation of motion of an ion particle is developed by means of the Lagrangian formulation. According to the numerical study, the displacement responses of an ionic particle can exhibit a stable periodic motion, verified by displacement responses and phase trajectory plots, which cements the prospect to trap an ion by a proposed electrostatic field within a stability parametric setting, l > 2a. Additionally, we find that the magnitude of the electrical charge of each ring and the ring radius, representing the ring size, significantly influence the frequency and velocity amplitude of the ion oscillation, where an ion particle tends to oscillate at a higher frequency if the charge concentration is greater, but the ring size becomes smaller. We also notice that the velocity amplitude of ion particle oscillation tends to rise when the charge concentration increases, while the ring radius decreases. In future work, we will extend our study to a three-dimensional case to gain more insights and discover the realistic behavior of a trapped ion in a non-uniform electrostatic field, which might lead to the development of the experimental prototyping.

Fig. 1

(a) Electrostatic potential ϕ(r, θ) at the point of interest generated by an azimuthally symmetrical charge distribution ρ(r′, θ′). (b) Electrostatic potential ϕ(r, θ) at the point of interest created by an ionic ring at radial distance r and inclination angle θ in the polar spherical coordinate, ‖r-r′‖ =r·r+r′·r′-2r·r′, which results in Eq. (2).

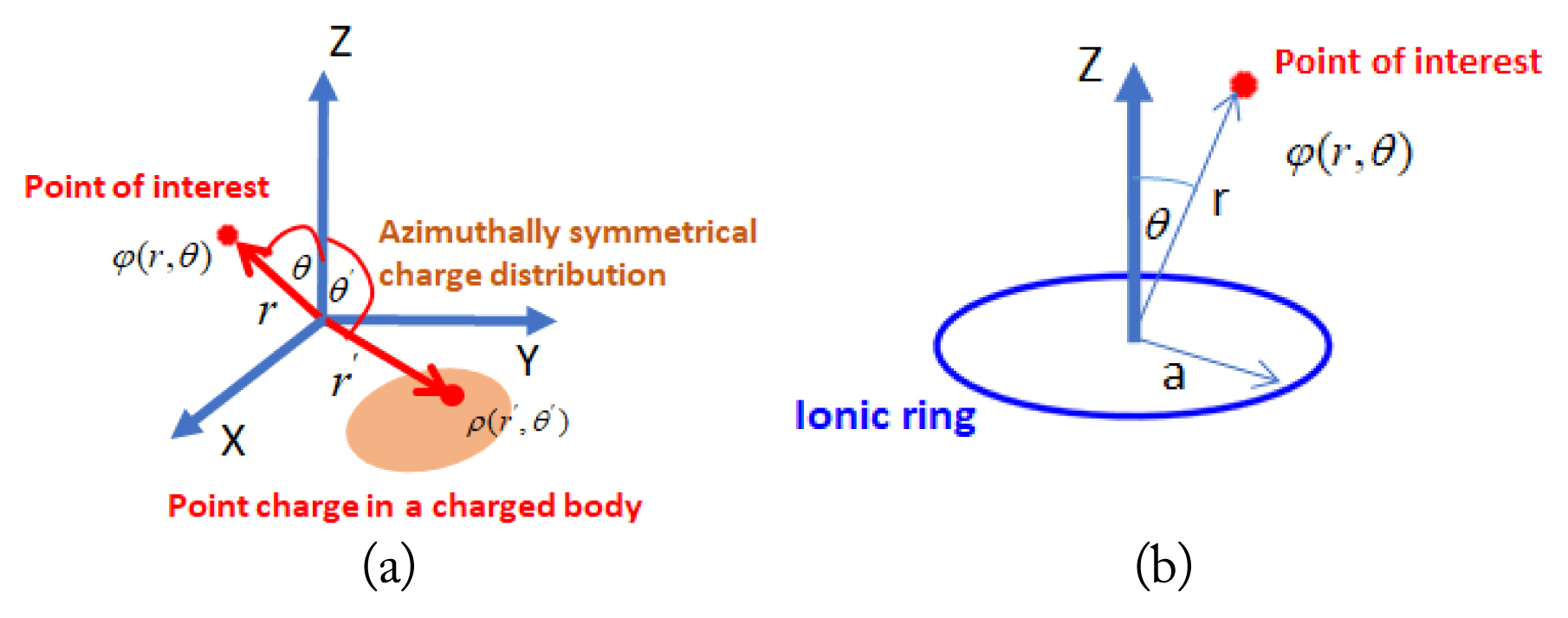
Fig. 2

Electrostatic potential ϕ_ring(r, θ) at the point of interest created by an ionic ring with radius a, r < c.

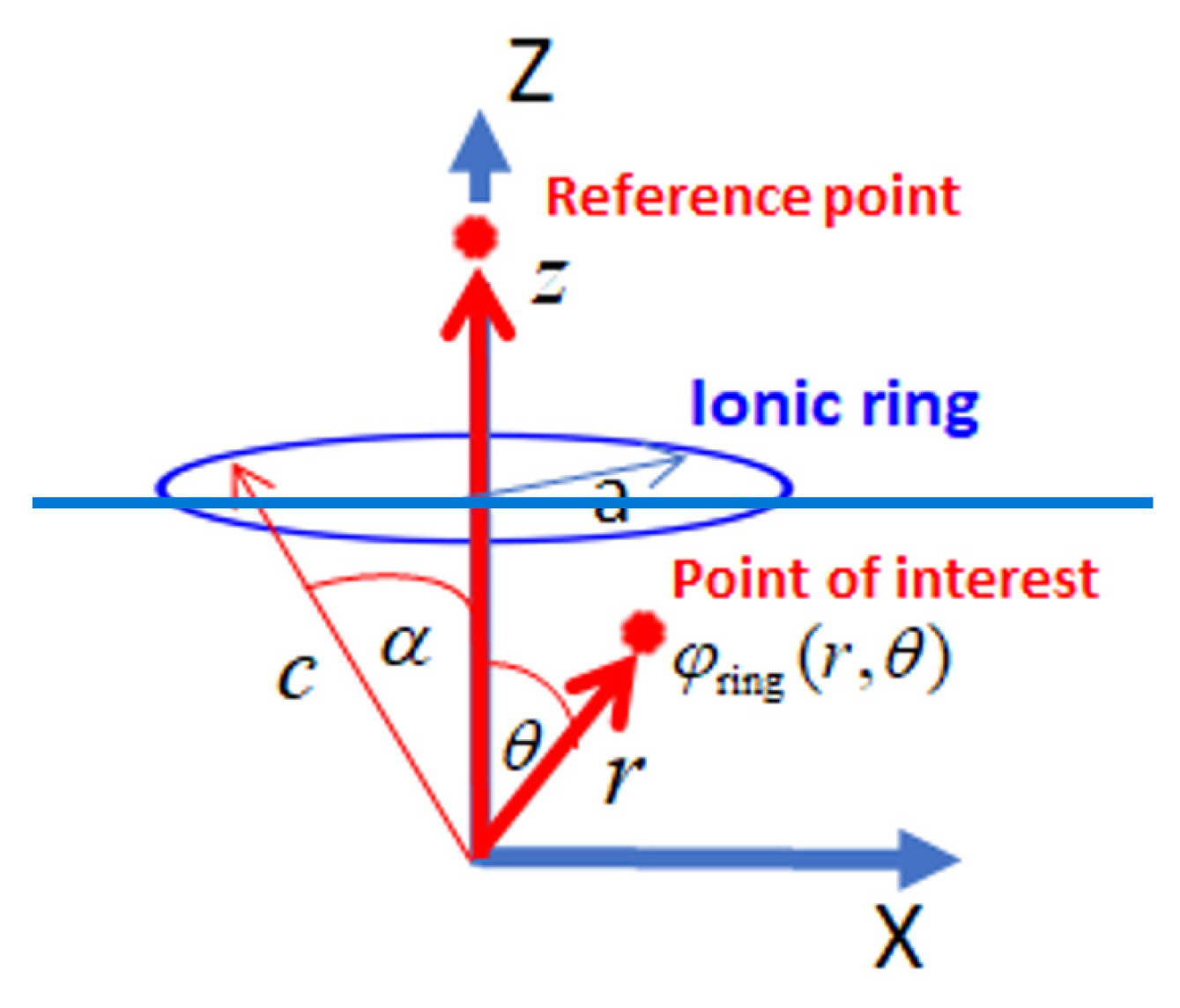
Fig. 3

(a) Schematic of a trapped ion confined in a non-uniform electrostatic field generated by two ionic rings; the imaginary tube is proposed to restrict the motion of a trapped ion in one dimension. (b) All related parameters and the coordinate orientation required to determine the electrostatic field in the z direction induced by two ionic rings, as well as the electrostatic potential for ring 1, can be given, using Eq. (11).

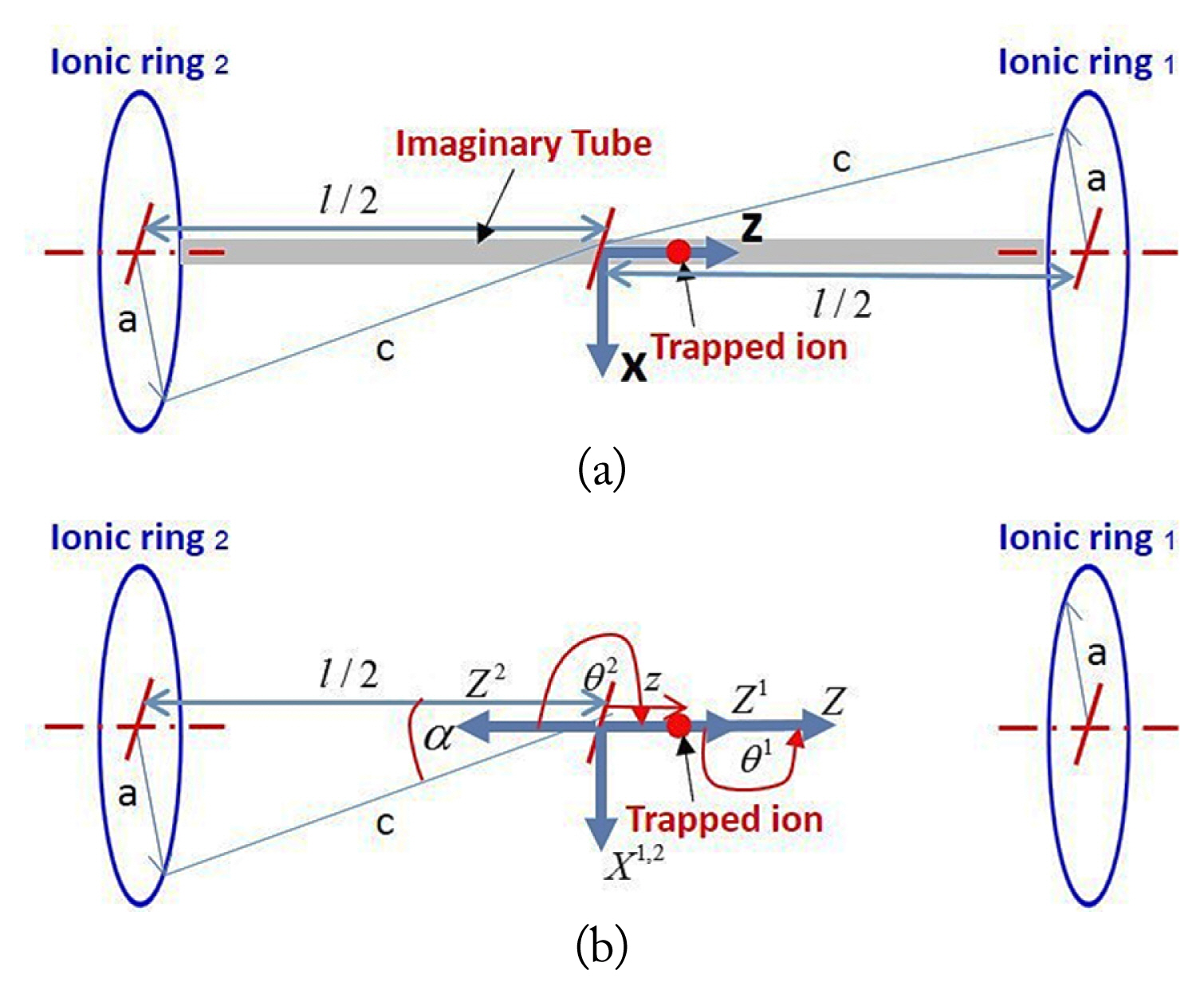
Fig. 4

Influence of charge ratio ζ on the free responses and the time interval of oscillation of a trapped ion in a nonuniform electrostatic field created by two ionic rings. (a) Free responses of a trapped ion in a one-dimensional motion in the z direction at ζ = 1, 5, and 10, with a = 0.03 m, where time t is in seconds and displacement z(t) is in meters. (b) Time interval of oscillation, T in seconds, at various charge ratio values, ζ ranging from 1 to 10 at a = 0.01, 0.02, and 0.03 m. Note that m = 6.64 × 10⁻²⁷ kg (the mass of one helium ion) and l = 0.09 m (the distance between ionic rings) are set in all simulations.

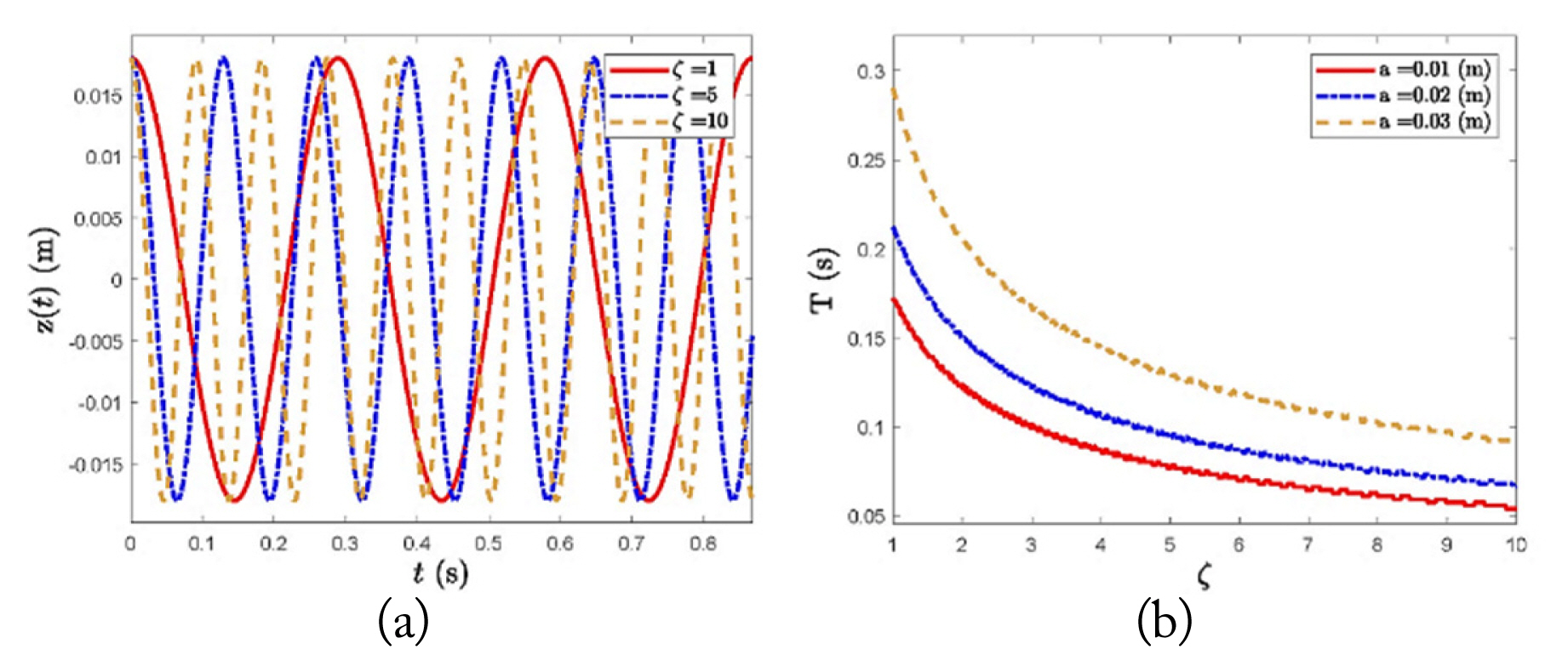
Fig. 5

Influence of charge ratio ζ on the phase space plot showing the phase trajectories of a trapped ion in a non-uniform electrostatic field created by two ionic rings at ζ = 1, 5, and 10, with a = 0.03 m, where time t is in seconds, displacement z(t) is in meters, and velocity ż(t) is in m/s. Note that m = 6.64 ×10⁻²⁷ kg (the mass of one helium ion) and l = 0.09 m (the distance between ionic rings) are set in all simulations.

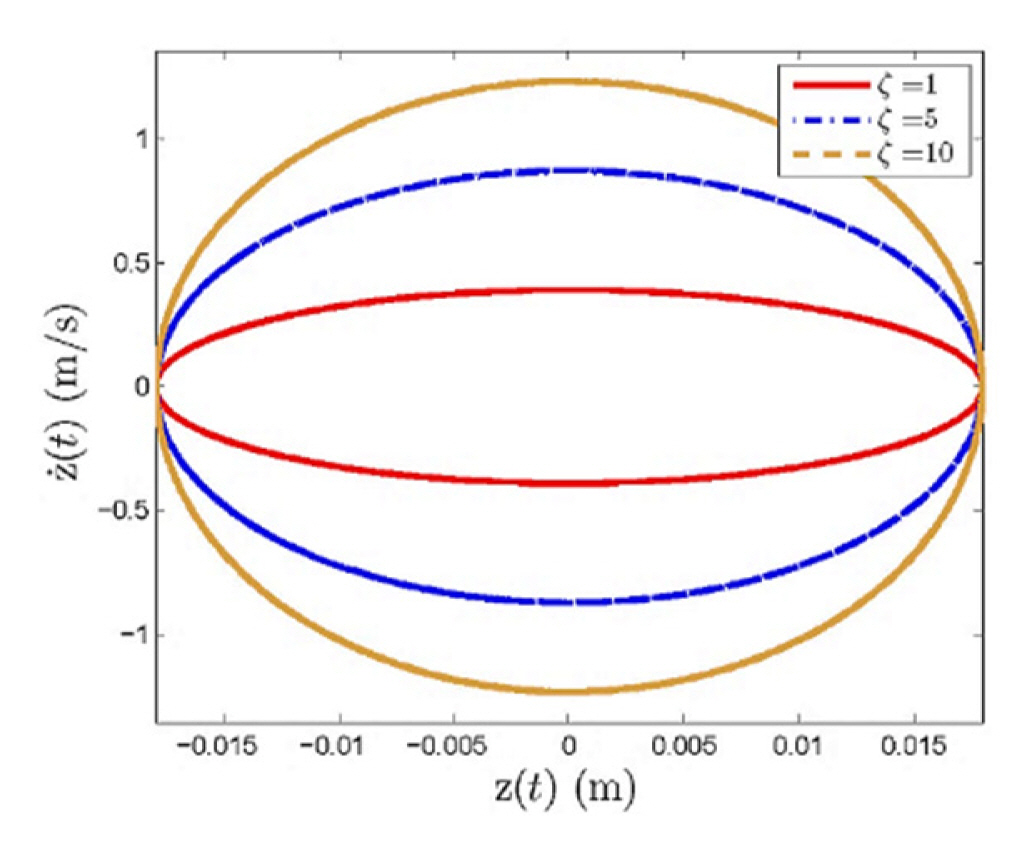
Fig. 6

Influence of charge ratio ζ on the velocity responses and the maximum velocity of oscillation of a trapped ion in a nonuniform electrostatic field created by two ionic rings. (a) Velocity responses of a trapped ion in a one-dimensional motion in the z direction at ζ = 1, 5, and 10, with a = 0.03 m, where velocity ż(t) is in m/s. (b) The maximum velocity of oscillation, żmax(t) in seconds, at various charge ratio values, ζ ranging from 1 to 10 at a = 0.01, 0.02, and 0.03 m. Note that m = 6.64 × 10⁻²⁷ kg (the mass of one helium ion) and l = 0.09 m (the distance between ionic rings) are set in all simulations.

Table 1

The first five Legendre polynomials

n	Legendre polynomial P_n(x)
0	P₀ = 1
1	P₁ = x
2	P2=12(3x2-1)
3^a	P3=15(5x3-3x)
4^a	P4=18(35x4-30x2+3)

^a These terms are omitted in this study as the small motion speculation has been made to develop the equation of motion for a trapped ion where the nonlinear effect is negligible. Eq. (5) is solely valid if the r < r^I condition has been met; otherwise, the electrostatic potential formulation will differ from Eq. (5). However, it can be found in Schwartz’s work [23], where the r > r^I condition is fulfilled, but it is beyond the scope of this study. An example of a single ionic ring under the azimuthal symmetry assumption is illustrated in Fig. 1(b). The electrostatic potential function determination for a single ionic ring is fully discussed in detail in the next section.

Table 2

Case studies of dynamic responses and other parametric studies

Case	Dynamic responses			Parametric studies

	ζ³	l⁴	a⁴	ζ³	l⁴	a⁴
1	1	0.09	0.03	1–10	0.09	0.01
2	5	0.09	0.03	1–10	0.09	0.02
3	10	0.09	0.03	1–10	0.09	0.03

l represents the distance between two ionic rings; a denotes a ring’s radius.

References

1. Y. Zhang, Y. Han, J. Wu, Y. Wang, J. Li, Q. Shi, X. Xu, and C. S. Hsu, "Comprehensive composition, structure, and size characterization for thiophene compounds in petroleum using ultrahigh-resolution mass spectrometry and trapped ion mobility spectrometry," Analytical Chemistry, vol. 93, no. 12, pp. 5089–5097, 2021. https://doi.org/10.1021/acs.analchem.0c04667

2. D. H. Mast, H. W. Liao, E. V. Romanova, and J. V. Sweedler, "Analysis of peptide stereochemistry in single cells by capillary electrophoresis–trapped ion mobility spectrometry mass spectrometry," Analytical Chemistry, vol. 93, no. 15, pp. 6205–6213, 2021. https://doi.org/10.1021/acs.analchem.1c00445

3. R. E. March, "An introduction to quadrupole ion trap mass spectrometry," Journal of Mass Spectrometry, vol. 32, no. 4, pp. 351–369, 1997. https://doi.org/10.1002/(sici)1096-9888(199704)32:4%3C351::aid-jms512%3E3.0.co;2-y

4. K. H. Dit Fouque, J. Moreno, J. D. Hegemann, S. Zirah, S. Rebuffat, and F. Fernandez-Lima, "Identification of lasso peptide topologies using native nanoelectrospray ionization-trapped ion mobility spectrometry–mass spectrometry," Analytical Chemistry, vol. 90, no. 8, pp. 5139–5146, 2018. https://doi.org/10.1021/acs.analchem.7b05230

5. M. E. Ridgeway, C. Bleiholder, M. Mann, and M. A. Park, "Trends in trapped ion mobility: mass spectrometry instrumentation," TrAC Trends in Analytical Chemistry, vol. 116, pp. 324–331, 2019. https://doi.org/10.1016/j.trac.2019.03.030

6. D. J. Wineland, C. Monroe, W. M. Itano, B. E. King, D. Leibfried, D. M. Meekhof, C. Myatt, and C. Wood, "Experimental primer on the trapped ion quantum computer," Fortschritte der Physik: Progress of Physics, vol. 46, no. 4–5, pp. 363–390, 1998. https://doi.org/10.1002/(SICI)1521-3978(199806)46:4/5%3C363::AID-PROP363%3E3.0.CO;2-4

7. D. J. Wineland, M. Barrett, J. Britton, J. Chiaverini, B. DeMarco, W. M. Itano et al., "Quantum information processing with trapped ions," Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, vol. 361, no. 1808, pp. 1349–1361, 2003. https://doi.org/10.1098/rsta.2003.1205

8. C. D. Bruzewicz, J. Chiaverini, R. McConnell, and J. M. Sage, "Trapped-ion quantum computing: progress and challenges," Applied Physics Reviews, vol. 6, no. 2, article no. 021314, 2019. https://doi.org/10.1063/1.5088164

9. J. M. Pino, J. M. Dreiling, C. Figgatt, J. P. Gaebler, S. A. Moses, M. S. Allman et al., "Demonstration of the trappedion quantum CCD computer architecture," Nature, vol. 592, no. 7853, pp. 209–213, 2021. https://doi.org/10.1038/s41586-021-03318-4

10. R. Weinstock, "On a fallacious proof of Earnshaw’s theorem," American Journal of Physics, vol. 44, no. 4, pp. 392–393, 1976. https://doi.org/10.1119/1.10449

11. L. S. Brown, "Quantum motion in a Paul trap," Physical Review Letters, vol. 66, no. 5, article no. 527, 1991. https://doi.org/10.1103/PhysRevLett.66.527

12. M. Drewsen and A. Broner, "Harmonic linear Paul trap: stability diagram and effective potentials," Physical Review A, vol. 62, no. 4, article no. 045401, 2000. https://doi.org/10.1103/PhysRevA.62.045401

13. C. J. Foot, Atomic Physics. Oxford, UK: Oxford University Press, 2004.

14. W. Paul, "Electromagnetic traps for charged and neutral particles," Reviews of Modern Physics, vol. 62, no. 3, article no. 531, 1990. https://doi.org/10.1103/RevModPhys.62.531

15. L. S. Brown and G. Gabrielse, "Geonium theory: physics of a single electron or ion in a Penning trap," Reviews of Modern Physics, vol. 58, no. 1, article no. 233, 1986. https://doi.org/10.1103/RevModPhys.58.233

16. M. Kretzschmar, "Particle motion in a Penning trap," European Journal of Physics, vol. 12, no. 5, article no. 240, 1991. https://doi.org/10.1088/0143-0807/12/5/010

17. M. D’Onofrio, Y. Xie, A. J. Rasmusson, E. Wolanski, J. Cui, and P. Richerme, "Radial two-dimensional ion crystals in a linear Paul trap," Physical Review Letters, vol. 127, no. 2, article no. 020503, 2021. https://doi.org/10.1103/PhysRevLett.127.020503

18. L. Dania, D. S. Bykov, M. Knoll, P. Mestres, and T. E. Northup, "Optical and electrical feedback cooling of a silica nanoparticle levitated in a Paul trap," Physical Review Research, vol. 3, no. 1, article no. 013018, 2021. https://doi.org/10.1103/PhysRevResearch.3.013018

19. J. Dilling, K. Blaum, M. Brodeur, and S. Eliseev, "Penningtrap mass measurements in atomic and nuclear physics," Annual Review of Nuclear and Particle Science, vol. 68, pp. 45–74, 2018. https://doi.org/10.1146/annurev-nucl-102711-094939

20. M. Niemann, T. Meiners, J. Mielke, M. J. Borchert, J. M. Cornejo, S. Ulmer, and C. Ospelkaus, "Cryogenic 9Be+ Penning trap for precision measurements with (anti-) protons," Measurement Science and Technology, vol. 31, no. 3, article no. 035003, 2019. https://doi.org/10.1088/1361-6501/ab5722

21. J. S. Murray and P. Politzer, "Molecular electrostatic potentials and noncovalent interactions," Wiley Interdisciplinary Reviews: Computational Molecular Science, vol. 7, no. 6, article no. e1326, 2017. https://doi.org/10.1002/wcms.1326

22. P. Politzer and J. S. Murray, "Electrostatics and polarization in σ-and π-hole noncovalent interactions: an overview," ChemPhysChem, vol. 21, no. 7, pp. 579–588, 2020. https://doi.org/10.1002/cphc.201900968

23. M. Schwartz, Principles of Electrodynamics. Newburyport, MA: Denver Publications, 2012.

24. D. J. Griffiths, "Introduction to electrodynamics," American Journal of Physics, vol. 73, no. 6, article no. 574, 2005. https://doi.org/10.1119/1.4766311

25. H. S. Cohl, A. R. P. Rau, J. E. Tohline, D. A. Browne, J. E. Cazes, and E. I. Barnes, "Useful alternative to the multipole expansion of 1/r potentials," Physical Review A, vol. 64, no. 5, article no. 052509, 2001. https://doi.org/10.1103/PhysRevA.64.052509

26. J. D. Jackson and R. F. Fox, "Classical electrodynamics," American Journal of Physics, vol. 67, no. 9, pp. 841–842, 1999. https://doi.org/10.1119/1.19136

27. L. D. Landau and E. M. Lifshits, Mechanics. Oxford, UK: Pergamon Press, 1960.

28. H. Goldstein, Classical Mechanics. San Francisco, CA: Addison-Wesley, 2002.

29. G. B. Arfken and H. J. Weber, Mathematical Methods for Physicists. 4th ed. San Diego, CA: Academic Press, 1995. https://doi.org/10.1016/C2009-1-28537-6

30. J. Em-Udom and N. Pisutha-Arnond, "Investigation of viscoelastic-creep and mechanical-hysteresis behaviors of hydrostatically stressed crystal using the phase field crystal method," Advances in Mathematical Physics, vol. 2020, article no. 2821402, 2020. https://doi.org/10.1155/2020/2821402

31. J. Em-Udom and N. Pisutha-Arnond, "Prediction of mechanical-hysteresis behavior and complex moduli using the phase field crystal method with modified pressure controlled dynamic equation," Materials Research Express, vol. 7, no. 1, article no. 015326, 2020. https://doi.org/10.1088/2053-1591/ab611f

32. F. Verhulst, Nonlinear Differential Equations and Dynamical Systems. Heidelberg, Germany: Springer, 2006.

33. S. H. Strogatz, Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton, FL: CRC Press, 2018.

34. S. Hassani, Mathematical Methods: For Students of Physics and Related Fields. 2nd ed. New York, NY: Springer, 2009.

35. H. Wang, Mathematics for Physicists. Singapore: World Scientific Publishing, 2017.

Biography

Jatupon Em-Udom earned B.Eng. and M.Eng. degrees in mechanical engineering from Chulalongkorn University in 2003 and 2007, respectively, and a D.Eng. degree in industrial engineering from King Mongkut’s Institute of Technology Ladkrabang, Bangkok, Thailand in 2020. He has been a post-doctoral fellow with the National Security and Dual-Use Technology Center, National Science and Technology Development Agency of Thailand. His research interests include the development of computational and numerical models of physics systems, such as material science, electrostatic fields, electromagnetic effects, and the mechatronic system, including robotics.

Biography

Nattapon Jaisumroum obtained a B.Eng. degree in electrical engineering from Mahanakorn University of Technology in 2000 and an M.S. degree in electrical engineering from King Mongkut’s University of Technology North Bangkok in 2012 and a Ph.D. degree in engineering from Thammasat University, Bangkok, Thailand in 2021. He has been a lecturer in the Sustainable Development of Technology Department, Faculty of Science & Technology, Thammasat University. His research interests include the development of electromagnetic fields, AI robotics, automation engineering, electricity, energy technology, IoT, and sustainable for SDGs.