I. Introduction
The finite-difference time-domain (FDTD) method has been popularly employed to analyze the electromagnetic (EM) problems in complex media [1–9]. The superiority of the FDTD method includes simplicity, robustness, and wideband analysis via a single simulation. It is very important to choose an appropriate dispersion model for an accurate EM analysis of media, considering dispersion characteristics. Various dispersion models, such as Drude, Debye, Lorentz, quadratic complex rational function (QCRF), complex conjugate pole residue (CCPR), and modified Lorentz (mLor), have been previously proposed to analyze EM propagation in dispersive media. Among the various dispersion models above, the mLor dispersion model is promising because it can unify the various dispersion models and also the computational efficiency of mLor FDTD simulation is superior to other dispersion-based FDTD simulations [10].
However, when using the conventional FDTD method for accurate EM wave analysis of very thin two-dimensional (2D) materials, enormous computing resources are required because a very small FDTD spatial grid should be used. Recently, the generalized sheet transition condition (GSTC) was successfully employed in FDTD modeling for a single-term Drude dispersion model, and it was reported that GSTC-FDTD can efficiently analyze the EM properties of 2D materials [11]. In this work, we present an efficient FDTD formulation for 2D materials with arbitrary dispersion models. Toward this purpose, we propose a GSTC-FDTD formulation based on a multiterm mLor dispersion model. Numerical examples are employed to show the excellence of the proposed FDTD formulation compared to the conventional FDTD method.
II. Modified Lorentz GSTC-FDTD Formulation
Consider that a 2D dispersive material is located at z = Ω in the xy plane of a rectangular coordinate system. A virtual electric FDTD grid, Ex(Ω−), or a virtual magnetic FDTD grid, Hy(Ω−), is introduced on both sides of z = Ω via the GSTC-FDTD method. The one-dimensional (1D) GSTC-FDTD update equations for Ex and Hy, respectively along the x- and y-directions in consideration of the virtual electric field grid and magnetic field grid, are as follows:
where ɛ0 and μ0 indicate the permittivity and the permeability of the free space, respectively. Note that Δt indicates the FDTD time step size, Δz indicates the FDTD grid size along the z direction, k indicates the space index along the z direction, and the superscript indicates the time index. The virtual electric field, Ex(Ω−), and the virtual magnetic field, Hy(Ω+), can be represented by the GSTC algorithm in the frequency domain (an ejωt time-dependence assumption) [12, 13] as
where
Note that χ represents the frequency-dependent surface susceptibility tensor, ω is the angular frequency, k0 is the propagation constant of free space,
Δ ϕ ξ = ϕ ξ t r - ( ϕ ξ i n c + ϕ ξ r e f ) , ϕ ξ , a v = ( ϕ ξ i n c + ϕ ξ r e f + ϕ ξ t r ) / 2
Substituting (9) and (10) into (1) and (2), respectively, and rearranging them, we get the following GSTC-FDTD update equations for Ex and Hy:
(11)
(12)
Let us consider the electromagnetic properties of 2D dispersive materials in the GSTC-FDTD formulation. Toward this purpose, we apply the mLor dispersion model to the GSTC-FDTD formulation. In this paper, for simplicity, we consider only the electrical polarization current density,
J ˜ e e , q x x ( ω )
where a0,q,a1,q,b0,q,b1,q, and b2,q are the mLor parameters for the q-th term. Using the multiterm mLor dispersion model for electric surface susceptibility,
J ˜ e e x x ( ω )
In the electrical polarization current density for the q-th term, by rearranging (14) and applying IFT, we obtain
By applying FDTD discretization to the above equation, we obtain
(16)
By rearranging (16), we obtain the following FDTD update equation for
J e e , q x x
In the above,
C a , q = 2 b 0 , q Δ t 2 - 8 b 2 , q b 0 , q Δ t 2 + 2 b 1 , q Δ t + 4 b 2 , q , C b , q = b 0 , q Δ t 2 - 2 b 1 , q Δ t + 4 b 2 , q b 0 , q Δ t 2 + 2 b 1 , q Δ t + 4 b 2 , q , C c , p = 2 a 0 , q ɛ 0 Δ t + 4 a 1 , q ɛ 0 b 0 , q Δ t 2 + 2 b 1 , q Δ t + 4 b 2 , q , C d , q = 8 a 1 , q ɛ 0 b 0 , q Δ t 2 + 2 b 1 , q Δ t + 4 b 2 , q , C e , q = 2 a 0 , q ɛ 0 Δ t - 4 a 1 , q ɛ 0 b 0 , q Δ t 2 + 2 b 1 , q Δ t + 4 b 2 , q E x , a v n + 1 = [ E x n + 1 ( k + 1 ) + E x n + 1 ( k ) ] / 2
(18)
It is noted that the FDTD update equation for Hy is the same as the conventional FDTD equation as follows:
In summary, the procedure for the proposed mLor GSTC-FDTD formulation is as follows:
III. Numerical Examples
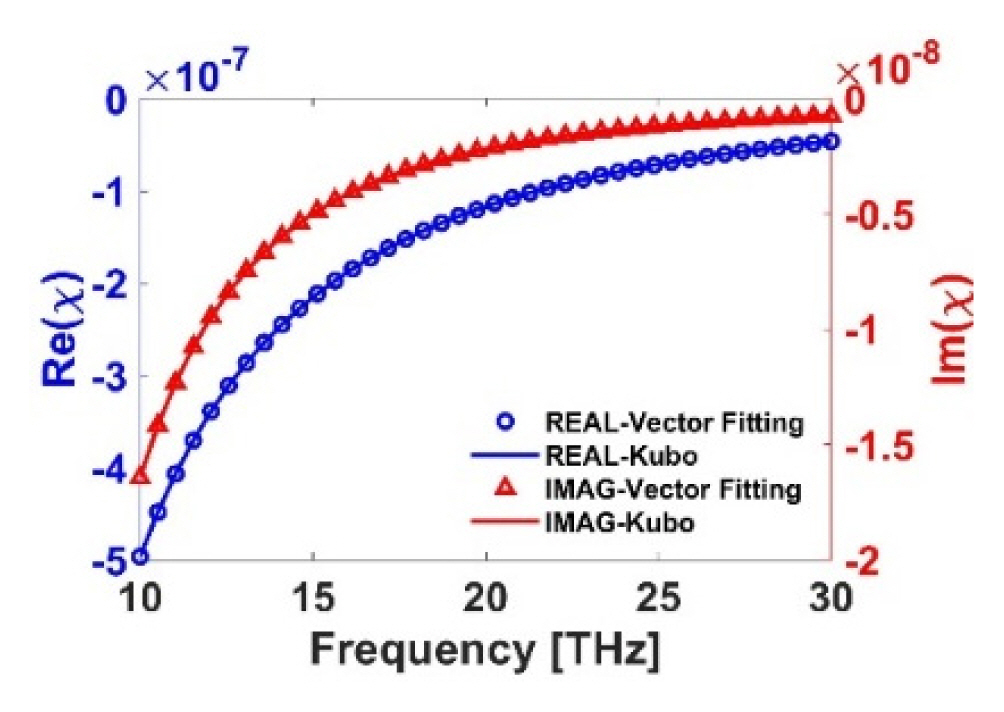
As proof of concept, in this work, we consider a popular 2D material, graphene, at 10–30 THz. Four-term pole-residue pairs are extracted using the vector fitting technique [14] for the surface conductivity of graphene, as described by the Kubo formula [15].
In this work, μc =150 mev, T = 300 K, and Γ=0.5 ps are used for the graphene parameters [16]. As shown in Fig. 1, the surface susceptibility calculated by the vector fitting method is in good agreement with the Kubo formula. Note that both the intraband and interband terms should be considered for the surface conductivity of graphene in the frequency range of interest; thus, a single-term Drude dispersion model-based GSTC-FDTD formulation [11] cannot be employed.
Table 1 indicates the fitted pole-residue pairs obtained by the CCPR vector fitting method. The first and second pole-residue pairs are real-valued, while the others are complex conjugates. The mLor parameters can be obtained by converting the CCPR parameters by
a 0 , q = - 2 R e ( p q r q * )
Next, we analyze the EM properties of graphene using FDTD simulations. In FDTD simulations, the 1D computational domain has a physical length of 1,000 nm along the z-direction, and a graphene sheet is located at the center of the computational domain. The entire FDTD domain includes 10-cell perfectly matched layers [17, 18] on both ends. We employ FDTD grid sizes of 1 nm, 2 nm, and 10 nm, and the corresponding FDTD time step size is set for the Courant-Friedrichs-Levy (CFL) stability condition.
A Gaussian-modulated sinewave with a bandwidth of 10–30 THz band is used for source excitation. Fig. 2 shows the reflection coefficient and the transmission coefficient of the graphene sheet. As shown in Fig. 2, the results of the mLor GSTC-FDTD simulation agree well with the theoretical values, regardless of FDTD grid size. However, the mLor FDTD [19] simulations are not in agreement with theoretical results [20] when the FDTD grid is equal to or larger than 2 nm. The reason is why the conventional mLor FDTD simulation for a large FDTD grid size is difficult to model the inside of a graphene sheet with a very thin thickness. However, the proposed mLor GSTC-FDTD simulation can model a very thin graphene sheet with a zero-thickness model; thus, accurate results can be obtained as long as the FDTD grid is about 15 times smaller than the wavelength of the surrounding material.
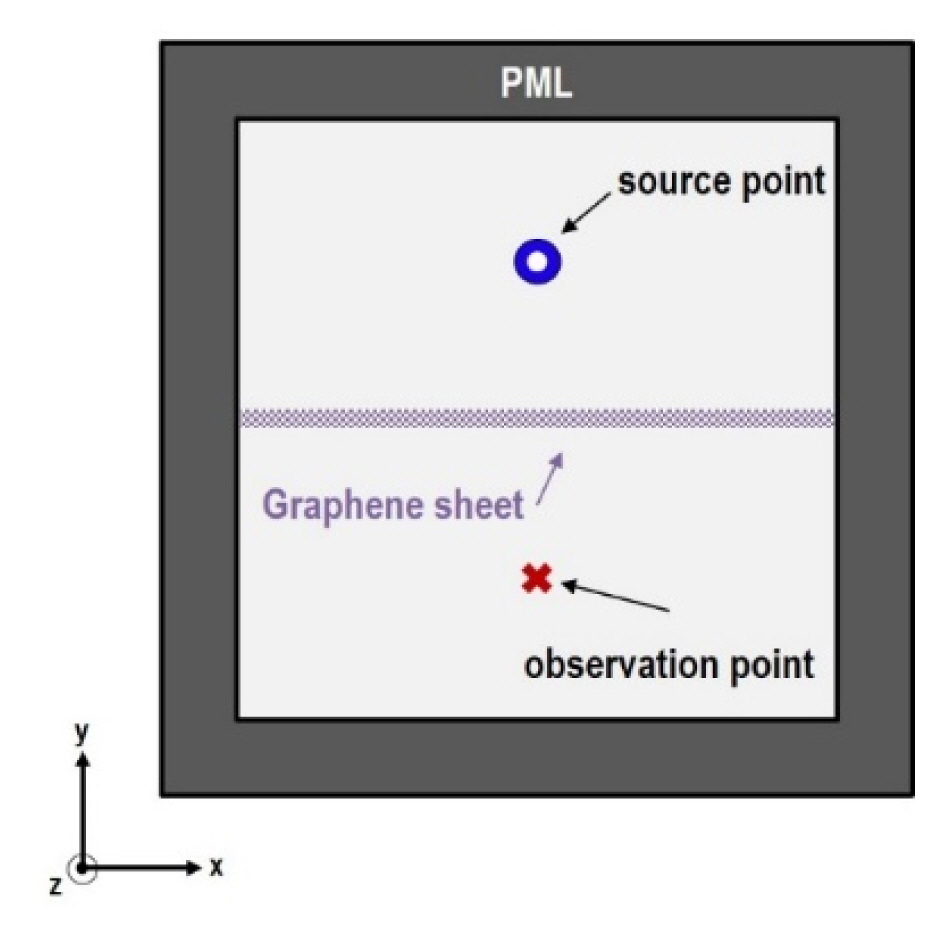
As the next example, we consider a 2D problem for a graphene sheet, and its geometry is depicted in Fig. 3. We employ the same FDTD grid sizes and the time step size as the 1D problem. The physical size of the computational domain is 1,000 nm × 1,000 nm, and 10-cell perfectly matched layers are considered. The z-directed magnetic current source with a bandwidth of 10–30 THz band is excited at 200 nm above the graphene sheet. The observation point is located at 100 nm below the graphene sheet and Hz is observed.
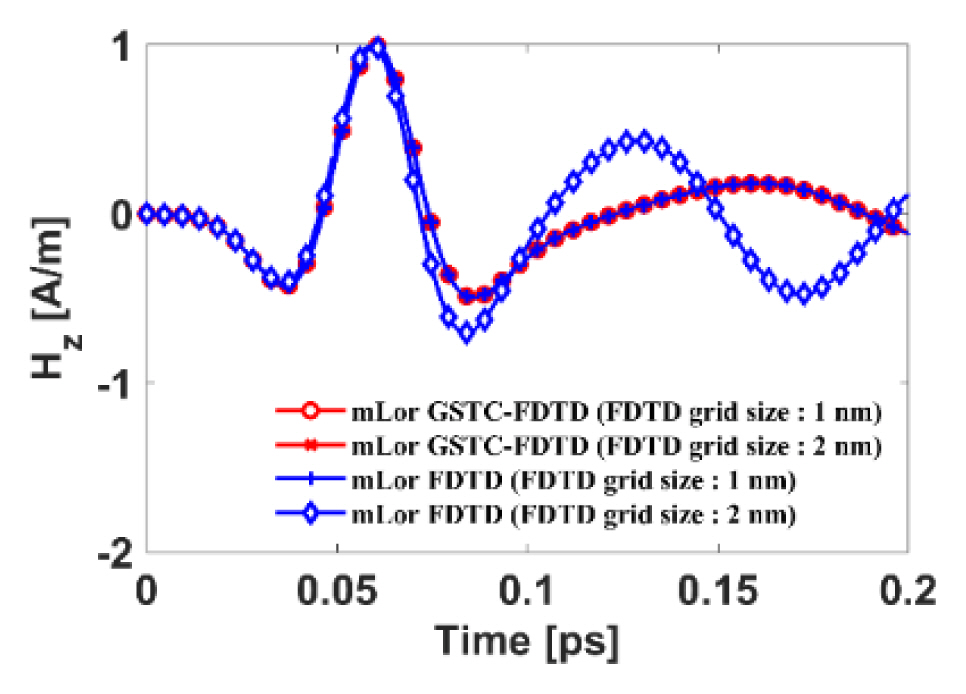
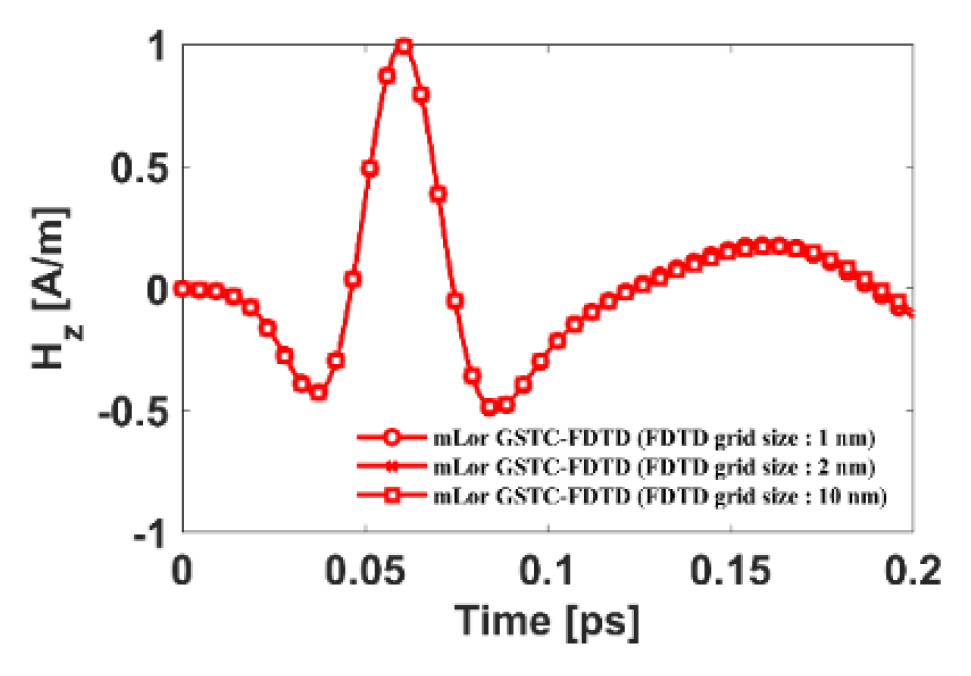
Fig. 4 shows the normalized magnetic fields of the two numerical results when the FDTD grid size is 1 nm and 2 nm. As shown in Fig. 4, the proposed mLor GSTC-FDTD simulation results are consistent with each other and are the same as the conventional mLor FDTD simulation result for the FDTD grid size of 1 nm. However, the accuracy of the mLor FDTD simulation deteriorates when the FDTD grid size is 2 nm, the same as in the 1D problem. Fig. 5 shows the mLor GSTC-FDTD simulation results when the FDTD grid size is 1 nm, 2 nm, and 10 nm. As shown in Fig. 5, it is observed again that the numerical results of the mLor GSTC-FDTD simulations are the same.
Table 2 summarizes the CPU times and memory storage necessary for accurate FDTD simulations: the mLor FDTD simulation with the FDTD grid size of 1 nm and the mLor GSTC-FDTD with the FDTD grid size of 10 nm. As shown in Table 2, the proposed mLor GSTC-FDTD simulation requires significantly less CPU time and memory storage requirements compared to its conventional FDTD counterpart.
IV. Conclusion
In this research work, we propose an efficient and unified GSTC-FDTD algorithm for the EM analysis of 2D dispersive materials. The mLor dispersion model and the GSTC algorithm are employed to derive the proposed FDTD update equations for dispersive 2D materials. It is shown that the surface susceptibility of graphene calculated by the vector fitting method in the THz band agrees with the analytical counterpart. Numerical examples are employed to demonstrate that the proposed mLor GSTC-FDTD formulation can accurately and efficiently analyze the EM characteristic of 2D dispersive media. It is observed that the computational efficiency of the proposed mLor GSTC-FDTD formulation is significantly higher than the conventional mLor FDTD formulation.