Inverse Design of Electromagnetic Metasurfaces Utilizing Infinite and Separate Latent Space Yielded by a Machine Learning-Based Generative Model
Article information
Abstract
This study proposes an inverse design framework for metasurfaces based on a neural network capable of generating infinite and continuous latent representations to fully span the electromagnetic metasurfaces (EMMS) property space. The inverse design of EMMS inherently poses the one-to-many mapping problem, since one set of electromagnetic properties can be provided by many different shapes of scatterers. Previous studies have addressed this issue by introducing machine learning-based generative models and regularization strategies. However, most of these approaches require highly complex operating configurations or external modules for preprocessing datasets. In contrast, this study aimed to construct a more streamlined and end-to-end solver by building a network to process multimodal datasets and then incorporating a classification scheme into the network. The validity of the idea was confirmed by comparing the accuracy of the results predicted by the proposed approach and the outcomes simulated using PSSFSS.
I. Introduction
Electromagnetic metasurfaces (EMMS) are composed of thin two-dimensional arrays of subwavelength-sized metallic unit cells that can manipulate the phase/magnitude response and polarization of electromagnetic waves at specific frequencies [1–4]. Owing to these capabilities, EMMS are used as spatial filters, polarizers, or microwave absorbers in broad applications that require the manipulation of electromagnetic waves or optical frequencies, such as communication systems, energy harvesting, and cloaking [5–10]. These unique and extraordinary functionalities are largely determined by the physical structures and material properties of the metasurfaces, which are judiciously selected or designed. More importantly, the potentially limitless pattern shapes of scatterers can significantly broaden the applicability of EMMS to extremely vast areas. In this context, the accurate geometric design of meta-atoms plays a crucial role in the successful construction of metasurfaces that implement targeted electromagnetic (EM) properties. However, conventional design processes [11, 12] that map unknown design parameters to specific EM properties through numerous iterations of fullwave simulations are painfully time consuming. Furthermore, the process relies heavily on a limited number of designers, with expertise in electromagnetism and intuitive insights derived from extensive experience, who can efficiently narrow down the high-dimensional solution space. In this context, the inverse design technique, which attempts to directly predict equivalent metasurfaces for specific scattering properties, has been attracting considerable attention from many interested researchers, the majority of whom have been encouraged by machine learning (ML)-based frameworks [13–23].
To address the inverse problem, the literature introduced generative ML techniques, such as generative adversarial network (GAN) [24] or variational autoencoder (VAE) [25], that learn potential subspaces able to semantically explain training datasets. Previous studies have developed inverse models comprising multiple sub-networks, such as encoder, decoder, generator, simulator, or predictor. These sub-networks typically conduct regression from the input data domains to the target data domains and are implemented using either a convolutional neural network (CNN) or a multilayer perceptron (MLP) in alignment with a specific training strategy. In [26], a VAE consisting of an encoder and decoder was employed for representation learning in data domains composed of scatterer shapes. It effectively expressed the original data with remarkably reduced latent codes. Notably, the learned latent space serves as a sample space that offers fictitious but plausible data that never existed in the training dataset. In this context, the dimension and distribution of latent variables, which pertain to the hyperparameters predefined by users, play a crucial role in capturing a small set of underlying information from input datasets in a low-dimensional space. Additionally, they contribute to the generation of new data by interpolating the feature spaces extracted from the training datasets. In contrast, while GAN attempts to estimate the probability distribution of target datasets in the same manner as VAE, it does not utilize an explicitly determined distribution for latent space. As a result, it does not involve a regularization scheme, such as the Kullback-Leibler (KL) divergence [27], for controlling the distribution of latent space (detailed in the following section). This neural network focuses on creating artificial but realistic data mimicking training datasets based on the logic devised for deceiving a sub-network, called a discriminator, instead of trying to minimize the reconstruction error relative to the training datasets. Notably, since the release of the original GAN [28], various derivatives have been actively developed to demonstrate the ability to faithfully generate stochastic variations of training samples in wide fields to acquire massive amounts of samples that are semantically similar to existing datasets.
From these brief descriptions of the salient characteristics of the two representative ML-based generative models, it is evident that VAE emerges as a more intriguing candidate for addressing the inverse problem, since the latent spaces of the VAE offer the opportunity to generate the desired output that can be continuously and smoothly controlled by a predefined density function, consequently helping in the interpolation of training datasets. Overall, this work demonstrates the possibility of a small number of discrete training samples to yield infinite and continuous latent space using VAE, using which brand new shapes of meta-atoms corresponding to desired EM properties can be optimally synthesized. Furthermore, an additionally designed network is employed to validate the reliability of the predicted outcomes.
The achievements of the current work, distinct from previously reported studies, lie in its construction of separated latent spaces based on the types of scatterers, which can contribute to a more faithful estimation of target data. Another contribution of this study is its proposed approach for accomplishing end-to-end inverse design without the help of an expensive external simulator. Although the applicability and capability of the proposed approach are limited by its small design configurations, these limitations can be addressed in future research by considering increased degrees-of-freedom for the designs.
The remainder of this paper is organized as follows: Section II presents a brief preliminary study of the concept of VAE and introduces related works on this topic, Section III details the primary concepts of the proposed framework, Section IV describes the experimental setup and analyzes the results, and Section V discusses the significance and limitations of this work, suggests future directions for study, and concludes this article.
II. ML-Based Inverse Design of Metasurfaces
This section outlines the fundamentals of the several ML-based inverse models designed to address the inverse problem in metasurface design. Subsequently, the novelty of the proposed approach is presented, highlighting its distinct perspectives as compared to existing works.
1. VAE for Inverse Design Process
A VAE consists of two sub-networks—an encoder, which typically reduces the dimensionality of input data, and a decoder, which reconstructs the input data from the reduced dimensional variables. An autoencoder (AE) [29] possesses this fundamental architecture, which enables the creation of a significantly reduced-dimensional hidden space between the bottleneck layers of its two sub-networks. The distance between samples in the latent space, constructed through identity mapping (perfectly reconstructing the original input), can capture semantic differences that remain concealed when using Euclidean distance in the original data domain. Notably, while an AE is usually utilized as a tool for feature extraction in classification problems or for dimensionality reduction in effective data compression, the VAE can also serve as a generative model by introducing stochastic variations to latent variables. The detailed structure of this function is illustrated in Fig. 1, where X, X̂, and z denote the input data, the reconstructed data of the input, and latent codes, respectively. The encoder of the first sub-network, denoted by E, is exploited to yield two intermediate variables, μ and σ2, representing the mean and variance of a Gaussian distribution, respectively. Theoretically, latent codes z should be directly sampled using μ and σ2 from the probability density function. However, in the given scenario, computing the derivatives becomes infeasible due to the randomness in the sampling step, which prevents the backpropagation of loss signals to previous layers. To address this problem, VAE employs a reparameterization trick by introducing a noise vector ɛ, randomly sampled from a normal distribution, and adding it to the variance σ2. This concept can be briefly expressed as follows:
where the symbol ⊙ indicates the element-wise product, also known as the Hadamard product. The latent space, consisting of variable z, is shaped by the KL divergence scheme, as stated earlier. Notably, the variables sampled from the latent space can generate new examples (X̂), which are most likely to exist in the original data (X). Furthermore, the weights and biases of the learnable parameters in the neural network are optimized by means of a minimization strategy of the objective function, defined below:
where the total loss of LVAE is a function pertaining to X of the input data, and the parameters of the two sub-networks, E and D, are denoted by φ and θ, respectively. The first term on the right-hand side represents the KL divergence, quantified as the difference between a posterior, fitted by optimizing φ in E, and a predefined prior. The second term serves as a metric to calculate the reconstruction error of X̂, generated by Dθ(z) in relation to the original data X. This metric can take the form of the mean squared error (MSE) or a binary cross-entropy (BCE), depending on whether the target data consist of real values or binary numbers.
The following subsection explores related research on this subject, especially focusing on how the standard VAE structure has been customized to address the inverse design of metasurfaces.
2. Related Work: Motivation of the Study
In [26, 30], the authors demonstrated the reliable reproducibility of the latent space achieved by VAE for new shapes of unit cells, justifying the applicability of their approaches in diverse scenarios. Notably, both works introduced an auxiliary network, termed the predictor, to tackle the one-to-many mapping problem occurring in an inverse design—one set of desired EM properties could be acquired by many different scatterer structures. The predictor is responsible for regularizing the latent variables learned through repetitive identity mapping of the source domain data, which might take the shape of either scatterers or EM properties. In other words, it is due to the effects of the predictor that the latent space can simultaneously represent the key features of two different data domains—scatterers and EM properties—thus, consequently being a vector in latent space that acts like an interpreter to translate the data of one domain into the data in the other domain. The architecture of the predictor can be realized using CNN or MLP.
Nonetheless, the noticeable points of difference between the two prior works are their choice of target and source domains for identity mapping in the VAE and for the regression of the predictor. Fang et al. [30] chose scatterer shapes as the datasets for conducting self-supervised learning in VAE, while EM properties were exploited as the target variables for the predictor model, and the latent variables determined by VAE were the input. The inverse model constructed by this training scheme presents various inverse design strategies working separately according to the meticulously devised criterion established for assessing the relevance of the outcomes. One of the most ideal scenarios for inverse design, assuming no failures, is as follows:
1. Prepare the desired EM properties,
2. Randomly draw initial values from the latent space,
3. Put the variable into the predictor network and obtain the predicted EM properties,
4. Compute the difference between the resulting EM properties and the desired ones by running a particle swarm optimization (PSO) algorithm,
5. Update the latent variables based on the optimization tactic of the PSO,
6. Repeat this process until a preset tolerance or an iteration number is reached.
In contrast to the strategy adopted in [30], the authors in [26] employed the EM properties for learning latent representation, while the pattern shapes of the metasurfaces were utilized as input for the predictor performing the regression to predict latent variables. Interestingly, latent variables learned by VAE serve as label data for the output of the predictor network. The learning rule for this setup can be expressed as follows:
where θ and K denote a set of parameters of the predictor model and the dimension of the vectors, respectively, while 〈 ·, ·〉 indicates the Euclidean distance of the two vectors. This framework estimates a new metasurface design for a set of desired EM properties by jointly operating the optimization process of the inverse problem and the forward design process, taking advantage of the latent presentation that concurrently retains the common nature of both domains involved.
The two exemplified frameworks have been proven to satisfy diverse inverse design requests, maintaining high accuracy in a wide range of applications. Moreover, they offer valuable insights into the successful adoption of the ML-based inverse design approach for the synthesis of metasurfaces. However, despite their remarkable achievements, the previous works are characterized by some arguable limitations, such as their need for vast amounts of training datasets, the usage of a dedicated external simulator, and the high complexity of operation involved in achieving satisfactory inverse design. To address these challenges, the current study focuses on developing a more streamlined end-to-end design approach that is both generally and readily applicable without the need for assistance from an external simulator or for considering complex options in the operational process.
3. The State-of-the-Art Proposed Method
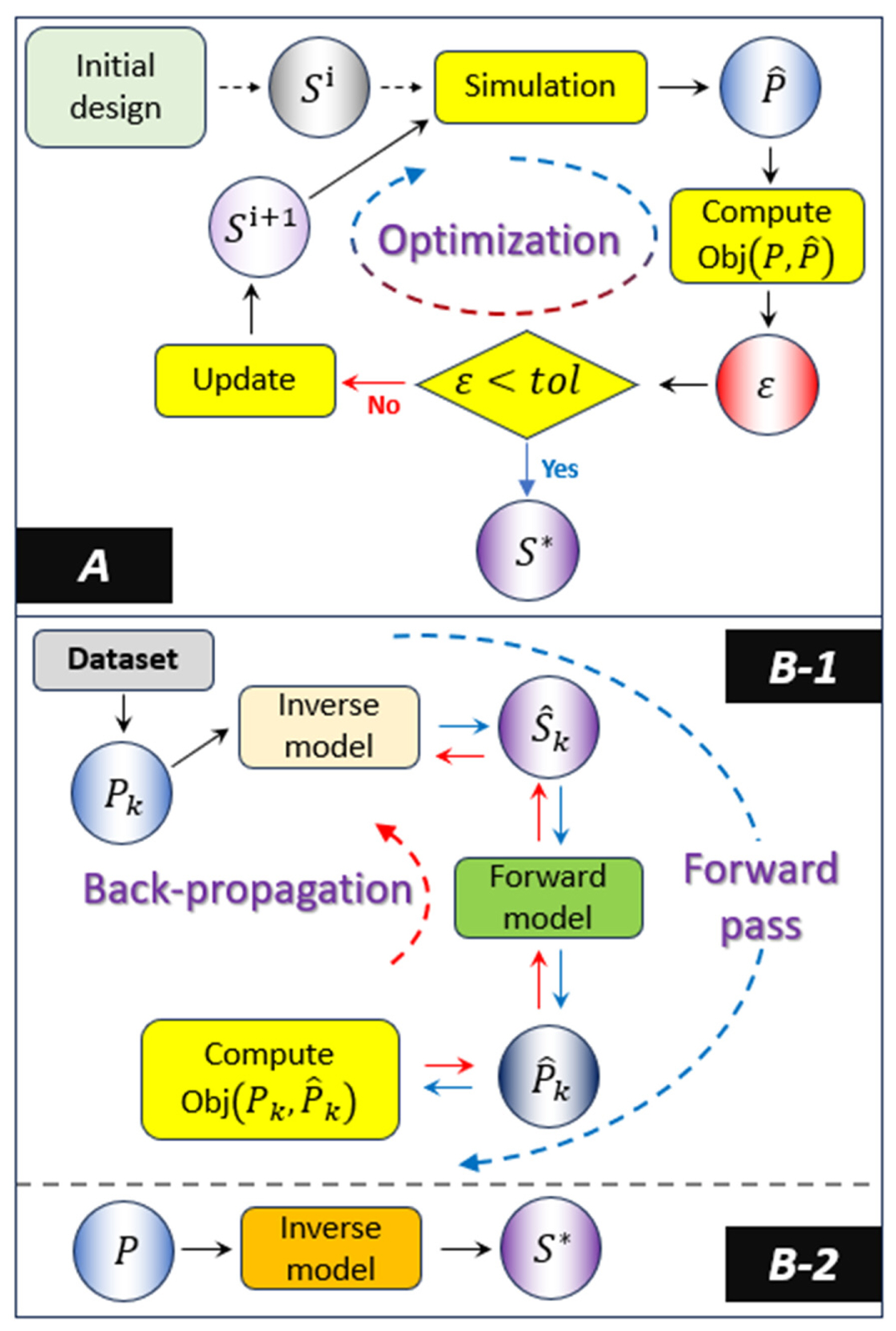
One of the significant advantages of ML-based inverse design methods relative to the conventional metasurface design process is that it does not need to conduct a brute force search by repeating full-wave simulations until the globally optimal solution is reached. However, to attain the benefits mentioned above in the design stage, data-driven approaches cost commensurate efforts—adequate data preparation, appropriate network design, and a robust validation process—in the model construction stage. The pros and cons of both concerned frameworks can be observed in Fig. 2, where block A visualizes the conventional design process and blocks B-1 and B-2 show the training phase and inference phase of an ML-based inverse design method, respectively. The symbols S and P represent the digital data corresponding to scatterer shapes and EM properties. It is evident that although the scheme in A does not require the preparation of a huge amount of datasets, it has to undergo many cycles of simulation at every design step. On the contrary, ML frameworks are able to markedly expedite the design process, as demonstrated in B-2, provided reliable neural networks are built in the B-1 learning phase. Nevertheless, the workflow of the inverse design depicted in B-2 may be considered ideal or extremely simplified, given the high degree-of-freedom exhibited by EMMS behavior, which varies with the design configuration. Moreover, the topology of the design space does not allow for the prediction of a unique solution. As a result, previous works were compelled to assume complex situations and set extra plans to address exceptional cases, due to which these frameworks require either an external simulator or the intervention of a human user. Inspired by the basic ideas enshrined in these existing works, the current study aims to develop a fully automated end-to-end ML-based inverse design method from scratch. To achieve this goal, additional useful information related to the geometry of EMMS, such as their types and dimension parameters, was employed. Furthermore, the architecture of the neural network was designed to reflect the roles pertaining to the additional information. Moreover, this work built separate latent spaces according to the types of EMMS to possibly predict equivalent EMMS shapes more precisely, owing to the reduction of ambiguity among the latent variables. The details are described in the next section.
III. VAE Constructing Multiple Latent Spaces
The notations for the symbols used to denote the variables and networks in this paper are provided in Table A1 of Appendix. In addition, the network structures of the VAE employed in this study for the inverse design are detailed in Table A2.
1. Data Preparation and Computing Configuration
The success of a data-driven approach is significantly influenced by the size of the training dataset and its relevance to the problem that users are facing, since weights in neural networks are fitted by interacting with features extracted from the dataset. To optimize the weights of a neural network, supervised-learning models utilize the loss signals yielded in the course of mapping the input data to the specified target data—a process referred to as function approximation. Therefore, to allow the function to faithfully relate two different domains, the pairs of input and output data should be informative and straightforward. Based on the above factors, the basic idea for synthesizing the training dataset used in this study was inspired by [26]. Furthermore, for the sake of accomplishing a more favorable function approximation, two additional data types—the class of the data and a set of numbers characterizing the geometry of the scatterer—were employed alongside the scatterer shapes and EM properties. These additional data not only provide increased information but can also be used to validate the results predicted by the proposed approach.
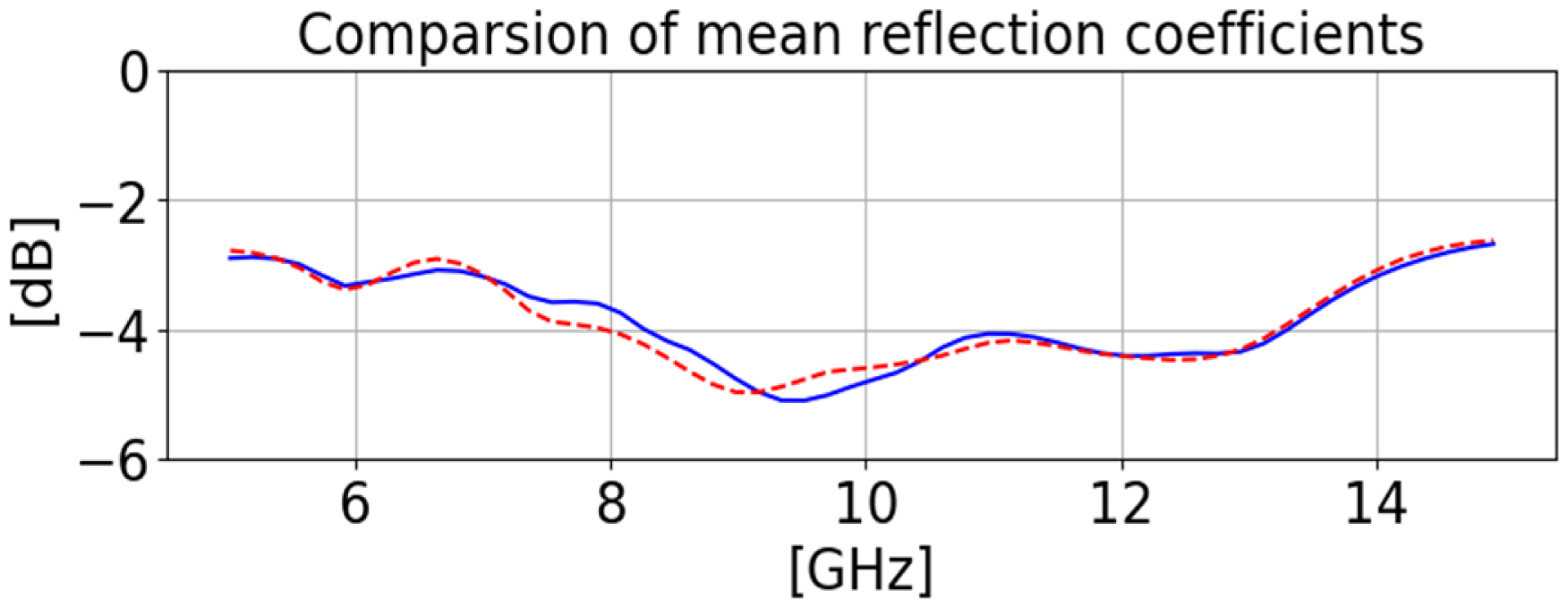
Meanwhile, the synthetic datasets were produced by PSS-FSS—a free and open-source code written in Julia programming language that was developed to design and simulate polarization selective surfaces (PSSs) and frequency selective surfaces (FSSs). Notably, to synthesize certain types of metasurfaces, PSSFSS requires several parameters to define the concerned shapes and materials. In this study, the additional data were used as the input arguments, based on which a comparison of the shapes of the scatterers acquired from the proposed method and from the PSSFSS can be conducted. Fig. 3 depicts the relationship among the four individual datasets, where C and D, corresponding to the additional dataset, are the 6-dimensional vectors specifying the geometry of shapes and categorical variables of one-hot encoding differentiating four classes of scatterer shapes, respectively. The denotations of S and P are the same as in the definition provided in Section II. In terms of data type, S is a 52×52 matrix consisting of elements with 1 representing a metallic area or 0 otherwise, while P is a vector having the length of 56. As stated earlier, while an inverse model aims to predict a corresponding S in terms of a desired P, the proposed approach seeks improvement in prediction accuracy by adding C and D to the canonical inverse process. Furthermore, the synthetic datasets were created by increasing each dimension of D(d1,,,d6) at uniform intervals with respect to four categories C(c1,,,c4) of surface shapes, i.e., Jerusalem cross (JC) patch, loaded cross (LC) patch, JC slot, and LC slot. Notably, the patches and slots were distinguished by identifying whether or not their shapes were composed of metallic material. The values for S and P obtained by the mean of PSSFSS are displayed in Fig. 4, where P considers only the reflection coefficients of EMMS.
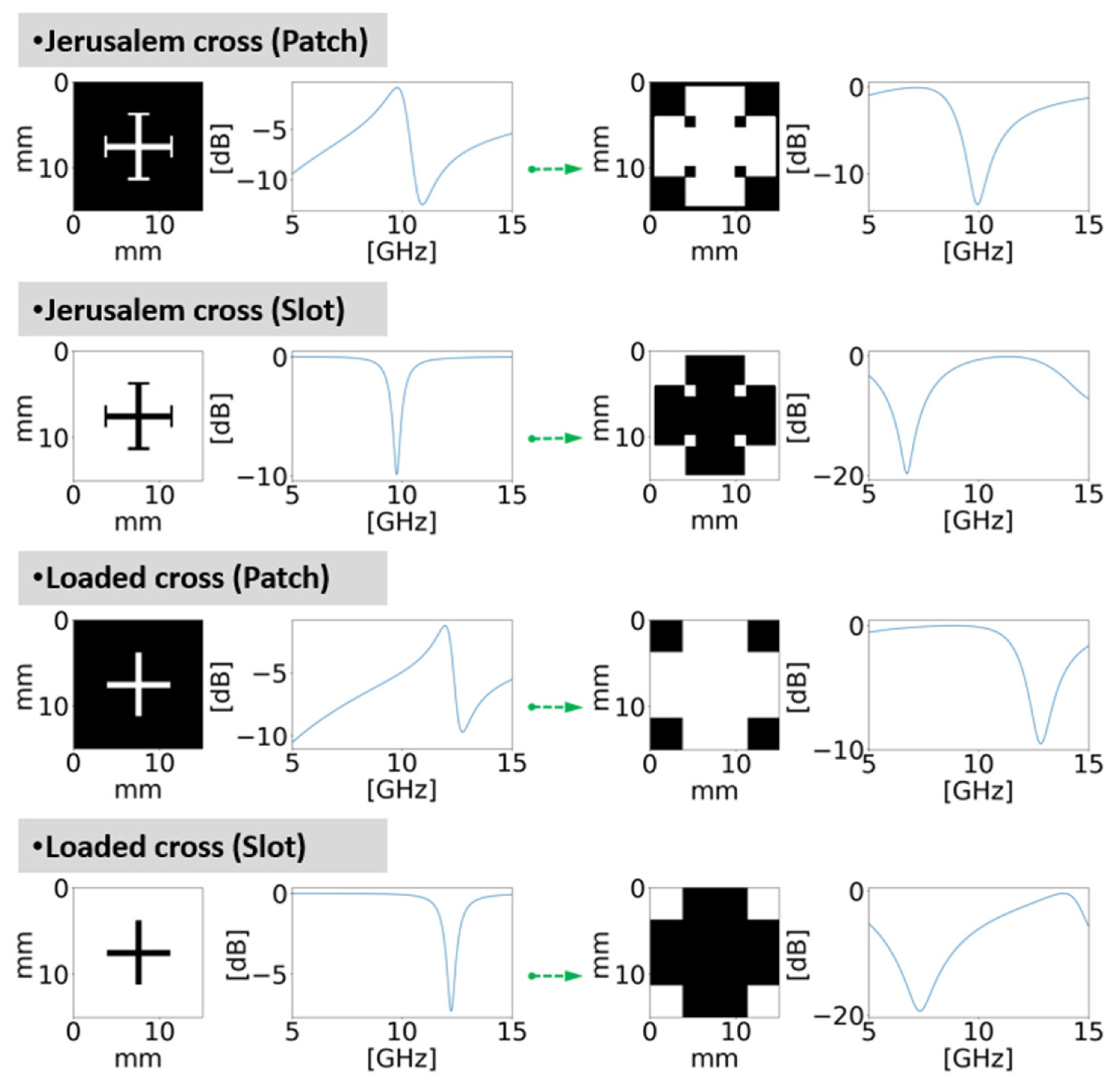
Four types of scatterer shapes generated by slightly changing the dimensions at a constant increment. The graphs display the reflection coefficients relative to the corresponding scatterer shapes in dB scale.
In addition, the parameters for the substrate material on which the meta-atom was placed had the same specifications as all PSSFSS simulations, with permittivity, loss tangent, and thickness of 4.4, 0.02, and 1.5 mm, respectively. The total number of datasets generated was 2,000, which was further divided at a ratio of 4 to 1 for training and testing whether each type of scatterer was evenly distributed, respectively.
2. Proposed Network
The framework proposed in this study follows a cascade structure in which the sub-networks—encoder (En), generator (Ge), and decoder (De)—are sequentially connected, as exhibited in Fig. 5. The most significant difference of this framework from the standard VAE illustrated in Fig. 1 is the generator (Ge) positioned between the latent variables z and the decoder (De), which plays a pivotal role in converting simple identity mapping from P to P’ into a joint learning neural network comprised of the inverse and forward models. Notably, during the training phase, the latent space learns the salient features shared by both the EM properties (P) and the design parameters of the metasurfaces (C and D). The learnt representation can continuously and infinitely span the feature space owing to the promising capability of VAE learning, although the current study used a discrete and small amount of training dataset, as stated in the previous subsection. Consequently, after terminating the training phase, z and the generator (Ge) were detached from the whole network and employed in an inverse design method. In this context, it should be noted that the generator (Ge*) yielding S’ contributed only to reliably constructing the latent representation z. The output S’ was not utilized in the following networks, since C and D were adopted as parameters determining the shapes of the scatterers and not S. Fig. 3 justifies this strategy. In fact, it was expected that the loss signal measuring the discrepancy between the estimated S’ and the true S will have an effect on regulating the latent space because S possesses the equivalent visual information for the geometry defined by C and D. Similarly, the auxiliary output S’’ of the decoder (De) predicting P plays the same role of imposing a constraint. Regarding the input and output datasets of the decoder (De), interestingly, it was observed that the network (De) carried out identical functions as the simulator PSSFSS, as depicted in Figure 3. Moreover, this study intended to enhance the fidelity of the generator (Ge) by evaluating the outcomes of the inverse design during the training phase. To achieve this, the decoder (De) was devised to learn the functions of the PSSFSS producing the shapes S for scatterers with respect to the given C and D and then predict the EM properties P. Therefore, the updated rule of weights in the entire network can be expressed as follows:

Architecture of the neural network devised in this work. Encoder (En) estimates, latent variables z, input data P, and z are fed into the generator (Ge). Its outputs, C’ and D’, are exploited for predicting P.
where LTotal indicates the weighted sum of the losses calculated by all involved loss functions with respect to the total number of data U, Θ denotes all learnable weights in the entire network,
 is a generic term representing all kinds of training datasets, while α and β are the hyperparameters tuned by the user. Furthermore, in the second row of Eq. (4)LKL is equal to the first term on the right-hand side in Eq. (2), while LRE constitutes three loss functions of the network—Ge, Ge*, and De—as follows:
is a generic term representing all kinds of training datasets, while α and β are the hyperparameters tuned by the user. Furthermore, in the second row of Eq. (4)LKL is equal to the first term on the right-hand side in Eq. (2), while LRE constitutes three loss functions of the network—Ge, Ge*, and De—as follows:
where LG* represents the cross-entropy loss obtained on computing the loss of estimates and the ground truth, while LG and LD are the loss functions obtained on computing both the cross-entropy and the mean squared. Notably, the types of loss functions were determined according to the data formats defined in the previous subsection.
3. Separately Distributed Latent Representations according to Specific Scatterer Types
As mentioned before, the dimension parameters of the datasets were synthesized based on four preset primitive patterns: JC (patch), JC (slot), LC (patch), and LC (slot). As a result, the frequency responses of each type of scatterer changed gradually, corresponding to alterations in the dimension parameters. However, the crucial characteristics, i.e., band pass, band stop, and bandwidth of the frequency response, were dominated by the type of primitive pattern. In this regard, identifying the type of scatterers prior to predicting their shapes based on a desired EM property could help enhance prediction accuracy. Along these lines, the authors of [21] proposed a classification for scatterer topologies by conducting principal component analysis (PCA) using a support vector machine (SVM), which represents a great achievement in the development of the inverse design method. Nonetheless, while this advanced approach carried out the classification using external modules, this study attempted to realize an end-to-end inverse design model by developing a neural network incorporating the classification process. The core idea was to utilize the separately distributed latent spaces illustrated in Fig. 6, constructed during the training phase, and operate them at four different KL divergence terms relative to each class, using the following equation:
where N implies that the Gaussian distribution is fitted by μl,c and
 symbolizes an indicator function whose output is 1 in the case of c = i, otherwise 0.
symbolizes an indicator function whose output is 1 in the case of c = i, otherwise 0.
IV. Experiments and Results
This section details the experimental setup and validates the results of the proposed approach based on three aspects.
1. Experiment Configuration
All simulations were conducted on a PC equipped with 32 GB RAM and an Intel Core i7-12700F CPU at 2.10 GHz. A total of 2,000 samples (500 samples per class across four classes) were synthesized, in accordance with the process described earlier. The samples were then divided into 1,600 training samples and 400 test samples, maintaining proportional representation across classes. The synthetic unit cells had a periodicity of 15 mm, and were postulated to activate at 10 GHz of the center frequency. In the training phase, the datasets were grouped into batches of 32 samples, using which the learnable parameters of the networks were updated for 1,000 epochs. Moreover, for evaluation, the metaatoms considered in the proposed inverse design method were simulated using PSSFSS, and the corresponding EM properties were estimated and then compared to the desired EM properties to establish the ground truth of the experiment. To measure prediction accuracy, this study employed the mean absolute error (MAE) of the computing differences between the two EM properties at each frequency point, which can be formulated as:
where P and P̂ are the desired and predicted EM properties, respectively, and i denotes one frequency point in 56 (N) points.
2. Reconstruction Accuracy of Test Datasets
The reconstruction accuracy of the proposed network was investigated using the test datasets. Fig. 7 describes the network pipeline for implementing identity mapping to the EM properties. In this test, the latent space was formed only by the estimated mean values without variances, indicating that the inference should be a deterministic process. As stated earlier, since S’’ was treated as just a dummy variable in the inference phase, the performance in this test was evaluated by calculating the MAE between P and P’. In Fig. 8, the reconstructed data, represented by red dotted lines, are compared to the reflection coefficients of the true samples, plotted using blue lines. A visual assessment of the figure shows consistency between the recovered data and the input samples. Furthermore, Fig. 9 compares the means of the 400 samples at every frequency point of the true samples (blue line) and the estimated results (red line). The MAE calculated for all frequency points was estimated to be 0.57. From the numerical results and visual assessment in Figs. 8 and 9, it is observed that the identity mapping process for the EM properties, as depicted in Fig. 7, exhibits satisfactory reconstruction accuracy, implying that the individual sub-networks had faithfully learned the relationships among the input-output data pairs involved in learning whole networks. The following subsection examines the prediction accuracy of the inverse design for scatterer shapes.
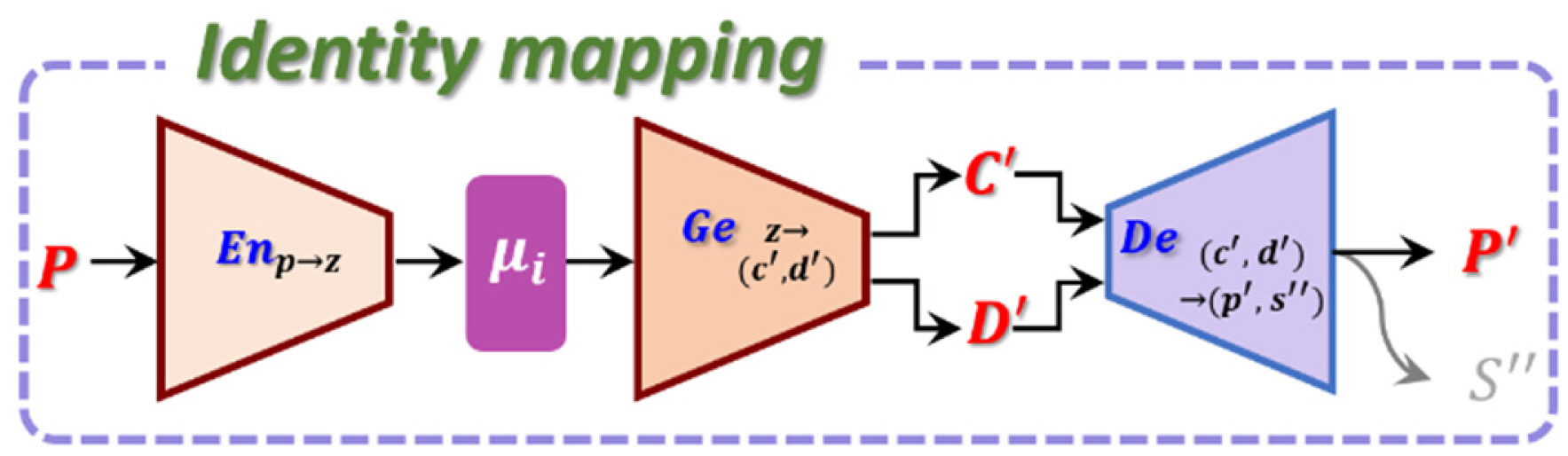
Schematic diagram showing the network pipeline for implementing identity mapping on the EM properties in the test datasets.
3. Evaluation of the Scatterers Reconstructed from Randomly Chosen Latent Variables
To confirm whether the latent variables continuously and smoothly spanned the sample space (Z) during the training phase while using a small amount of discrete training datasets, samples (zi’s) from the latent space were randomly drawn and fed into the PSSFSS and the decoder (De) through the generator (Ge), as shown in Fig. 10. The C’ and D’, estimated by the generator (Ge) using input zi, fully contained the geometric information necessary for synthesizing a metasurface using PSSFSS. As mentioned earlier, PSSFSS predicts P after producing S using inputs C and D. Hence, if the result of MAE(P,P’) is meaningfully tiny, it indicates that the latent space Z is able to accurately represent the infinite EM properties created following the rule by which the training datasets are synthesized. More specifically, assuming that the desired EM property is P̂(= P), P’ decoded from both C’ and D’ must be comparable to P̂ due to the small amount of error of MAE, while
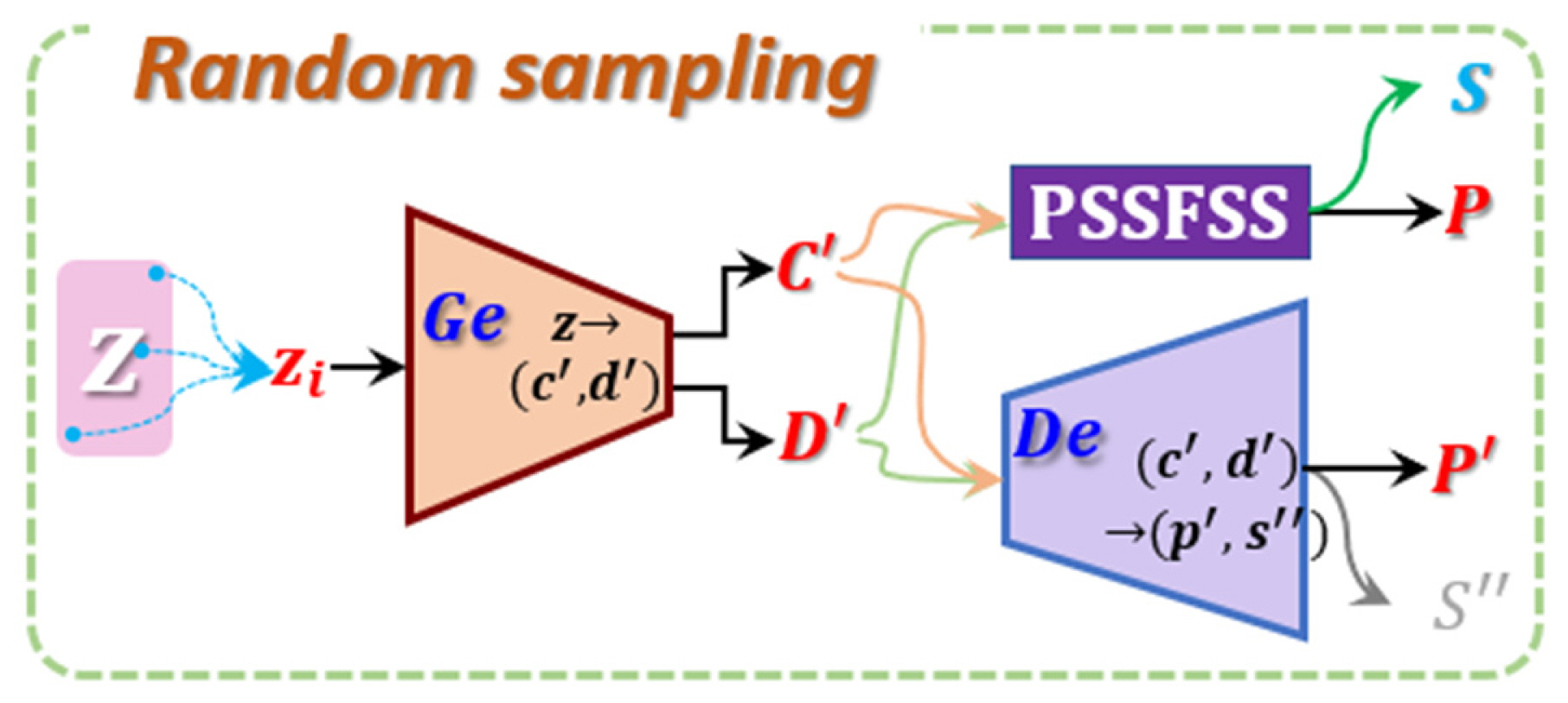
Randomly sampled variables (zi’s) pass the generator (Ge), which estimates the class and dimension, after which the outputs are fed into both the PSSFSS and the decoder (De).
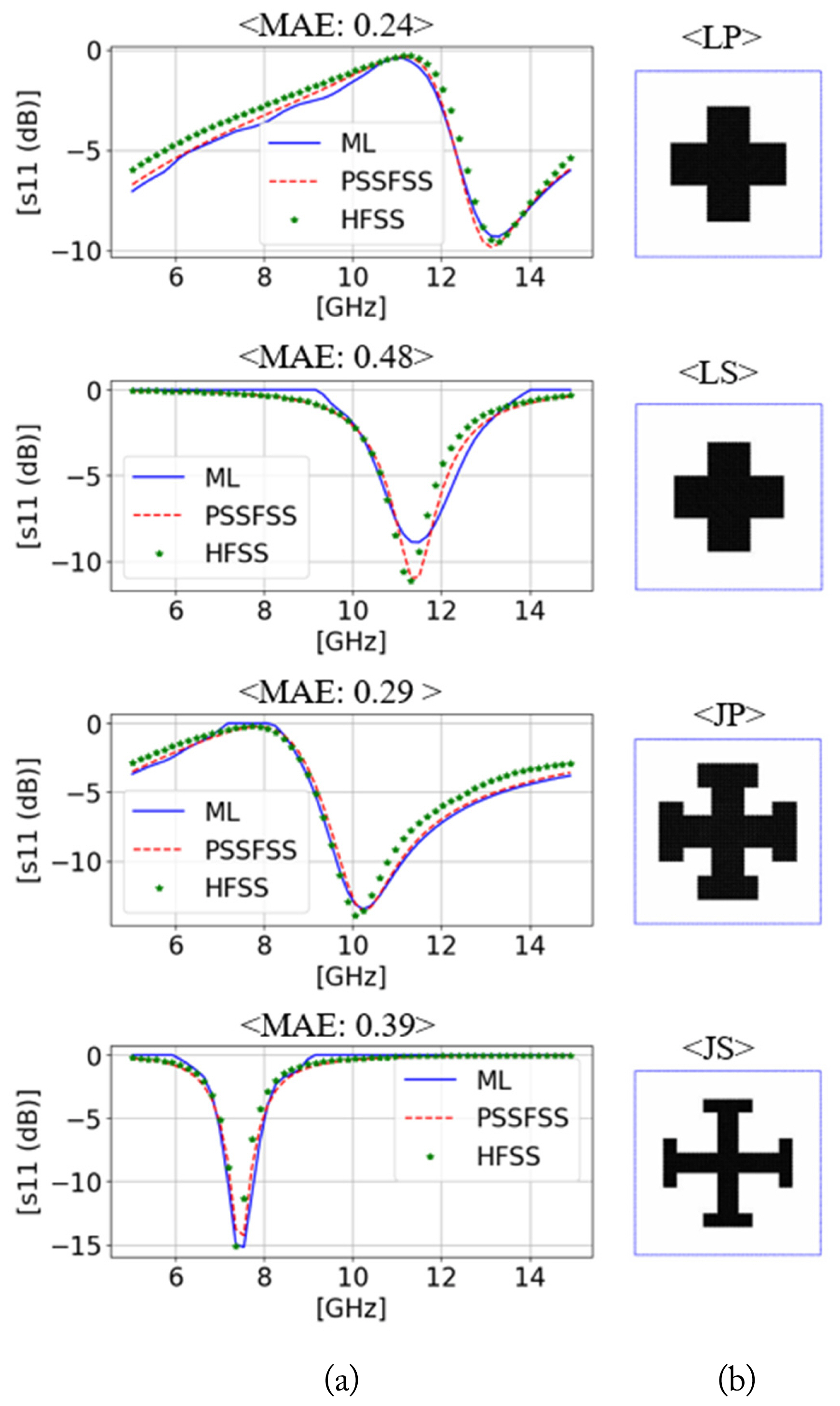
Results obtained on considering separately distributed latent spaces. The blue lines in column (a) are equivalent to the desired EM property found in the latent space Z, which corresponds to P’. Column (b) shows the inversely designed scatterer relative to P’ and yields the red dotted lines in (a) after PSSFSS simulation. In column (a), the green colored symbol “*” represents the results acquired from the HFSS simulation. The abbreviations on the images in column (b) indicate the types of scatters, as defined in Fig. 4.
4. Efficacy of Separately Distributed Latent Space
Finally, the impact of separately distributed latent spaces was investigated by comparing two cases—one with and one without the associated scheme. The test configurations were equal to the setup described in Sections IV-2 and IV-3. In the absence of the scheme, the reconstruction error (MAE) relative to the 400 test samples was 0.78, which was greater than the result acquired using separately distributed latent spaces by approximately 0.2. This implies that the model without the scheme demonstrated inferior estimation performance compared to the proposed method. In Fig. 12, the results obtained using the inverse design model with a single-distribution latent space are compared to those of PSSFSS and HFSS. The prediction error (MAE) of the variables sampled from the latent space is observed to be higher than the values computed with regard to the proposed approach in Fig. 11. Figs 13 and 14 clearly explain the consequences—the latent variables in Fig. 13 exhibit a single Gaussian distribution, while the variables in Fig. 14 show multiple peaks, similar to the Gaussian mixture model. Notably, this study intended to impose this characteristic of distribution on the latent space by taking advantage of Eq. (6) so that variables belonging to a certain class of scatterers could be sampled in terms of a unique mean value for the class. Using this strategy, variations in the EM properties for each class were clustered on a space independent from other classes, as illustrated in Fig. 6, making the process of searching relevant variables in the latent space more efficient and reliable. Nevertheless, in contrast to the expected outcome, the distributions exhibited in Fig. 14 do not characterize the perfect four Gaussian mixture model, with the distribution of Z[12] seemingly failing to learn the mixture distribution As mentioned before, only 2,000 samples were analyzed in this study, which were again split into 500 samples for each class. It is evident that the quantity of datasets used is inadequate for fully learning the intended distribution during the training phase. However, increasing the number of training datasets is likely to address this problem. The following section highlights the significance and contribution of the current study while also noting the limitations of the current work and directions for future research.

Results obtained on using latent space with single distribution. The blue lines in column (a) are equivalent to the desired EM property found in the latent space Z, which corresponds to P’. Column (b) shows the inversely designed scatterer relative to P’ and yields the red dotted lines in (a) after PSSFSS simulation. In column (a), the green colored symbol “*” represents the results acquired from the HFSS simulation. The abbreviations on the images in column (b) indicate the types of scatters, as defined in Fig. 4.
V. Discussion and Conclusion
In this study, latent variables produced by self-supervised learning in VAE successfully created a sample space capable of effectively expressing semantic representations that are typically entangled in the original data domain [33]. Furthermore, the latent space is smoothly and continuously spanned by the related variables owing to the KL divergence term that helps measure similarity losses between latent space distribution and the standard Gaussian function (zero mean and unit variance). As a result, the latent representation is able to infinitely yield new samples that do not exist in the original dataset but can potentially be found in the data domain.
In this context, previous works [26, 29] developed their own novel frameworks for the inverse design of metasurfaces, adopting VAE as a generative model and devising regularization manners to simultaneously extract and link features drawn from both the shape and scattering properties of an EMMS. Inspired by the achievements of these works, this study proposes a state-of-the-art methodology for streamlining and automating the structures proposed by these existing works by introducing a neural network architecture to process multimodal datasets and creating separately distributed latent space. The proposed network was constructed using the standard VAE, which was modified to deal with heterogeneous data formats and to regularize the latent space. The most noticeable difference between the proposed network and the existing ones is the generator network situated between the bottle neck layer and the decoder, which played a critical role in the formation of the inverse model and forward models. After completing the model training, the generator successfully predicted the shape of the scatterers using the input of latent variables. The output of the sub-network was then fed into the decoder to evaluate the predicted outcomes. In this context, the decoder functions as a simulator—validating the outcomes of the inverse model— similar to the operating mechanism of the PSSFSS. Consequently, the entire network was able to operate as an end-to-end model without relying on an external simulator.
Notably, the existing works [18, 21] introduced an extra step classifying the topologies of metasurfaces before employing an inverse design network to enhance learning performance. Consequently, these approaches necessitated the use of supplementary classification methods, such as PCA or SVM, alongside the inverse model. However, unlike previous works, the current study attempted to build a streamlined framework by integrating the scheme for carrying out the classification function into the neural network while also devising separately distributed latent space by modifying the KL divergence term to enable multiple-distribution learning. This novel idea made the operation of the entire framework simpler while also enhancing the prediction accuracy, as demonstrated in Section IV-4.
Nonetheless, it must be acknowledged that the applicability of the proposed approach is limited by the few types of scatterers considered in the training datasets and the extremely simple rules considered while synthesizing the datasets. It is well known that the number of parameters defining the geometric shapes and material properties of metasurfaces is far greater than those used in this study for generating the synthetic data for the simulation. Since design parameters encapsulate the physics governing the interaction between the scatterer and EM waves, it is imperative for a robust and widely applicable inverse design method to take the form of an ML model trained on an extensive dataset covering a diverse range of parameters and capable of accommodating all possible environmental conditions. However, data-driven approaches inevitably face challenges due to the lack of relevant datasets. Thus, instead of the exhaustive collection of necessary datasets, alternatives such as simple data augmentation tricks, transfer learning techniques, and generative models have been developed in the literature to circumvent this intrinsic problem [34]. Among these techniques, VAE is one of the most preferable methods for reproducing realistic datasets. Several variation models customized from the basic structure of the VAE have reported promising outcomes and exhibited great potential for use in the EMMS inverse design method.
In future studies, latent space learning in VAE should play a more crucial role in efficiently representing broad and complex design spaces by accounting for multilayer surfaces, surface thickness, various scatterer shapes, and other indispensable design parameters. In addition, the researchers plan to introduce more diverse multimodal datasets and design a more sophisticated network pipeline for processing heterogeneous datasets to achieve broader applications.
Acknowledgments
This work was supported in part by the Basic Science Research Program (Grant No. 2020R1I1A3057142), in part by the Priority Research Center Program through the National Research Foundation (Grant No. 2019R1A6A1A03032988), and in part by the National University Development Project of the Ministry of Education in 2023.
Appendices
References
Biography

Jong-Hoon Kim, https://orcid.org/0000-0001-9584-8917 received his master’s degree in biomedical engineering from the University of Bristol, Bristol, U.K., in 2016, and his Ph.D. degree in information and telecommunication from the University of Toulouse, Toulouse, France. From 2020 to 2022, he was a research professor at the Medical Convergence Center of Gachon Medicine College, Incheon, South Korea, where he was involved in the development of AI algorithms for the diagnosis and detection of lesions. In September 2022, he joined the Smart Natural Space Research Center of Kongju National University Cheonan, South Korea, as a research professor. His current research interests include developing new algorithms based on deep learning for detecting and recognizing objects from radar sensor images.

Ic-Pyo Hong, https://orcid.org/0000-0003-1875-5420 received his B.S., M.S., and Ph.D. degrees in electronics engineering from Yonsei University, Seoul, South Korea, in 1994, 1996, and 2000, respectively. From 2000 to 2003, he worked in the Information and Communication Division of Samsung Electronics Company, Suwon, South Korea, where he was a senior engineer involved in CDMA mobile research. Since 2003, he has been working in the Department of Information and Communication Engineering, Kongju National University, Cheonan, South Korea, where he is currently a professor. In 2006 and 2012, he was a visiting scholar at Texas A&M University, College Station, TX, USA, and Syracuse University, Syracuse, NY, USA, respectively. His research interests include intelligent reflecting surfaces, numerical techniques in electromagnetics, and periodic electromagnetic structures.