|
 |
- Search
| J. Electromagn. Eng. Sci > Volume 19(2); 2019 > Article |
|
Abstract
This paper presents a design methodology for wideband single-layered microwave absorbers with arbitrary absorption at the design center frequency using reactive Salisbury screens. The bandwidth of the absorber increases when the flatness of the reflection response at the design center frequency is maximized. Based on this observation, closed-form design formulas for wideband absorbers are derived. As they are scalable to any design frequency, wideband reactive screens can be systematically realized using two-dimensional periodic crossed-dipole structures patterned on a resistive sheet. Based on this method, a single-layered absorber with a 90% bandwidth improved to 124% of the design center frequency is presented. For the purpose of physical demonstration, an absorber with a design center frequency of 10 GHz is designed and fabricated using a silver nanowire resistive film with a surface resistance of 30 ╬®/square. The measured absorption shows a good agreement with both the calculation and the electromagnetic simulation.
A number of studies have developed thin and broadband absorbers that can be utilized for stealth applications and in the laboratory environment. Recent advancements in metamaterial research have opened up the possibility for metamaterial absorbers [1ŌĆō3]. However, the reported bandwidth of a metamaterial absorber remains far narrower than that of conventional Salisbury absorbers.
Salisbury absorbers are some of the most representative microwave absorbers. The simplest design of Salisbury absorbers has a resistive sheet of 377 ╬®/square placed at a distance of a quarter wavelength from a metallic plane [4, 5]. The bandwidth of the Salisbury screen is essentially limited by the frequency dependence of the sandwiched layer. A primitive way to enhance the bandwidth in a Salisbury screen is simply by using more resistive sheets spaced at the same distance (╬╗/4) apart [6]. These original structures, consisting of purely resistive sheets, a dielectric slab, and a ground plane, are referred to as Jaumann absorbers. A systematic design method of Jaumann absorbers to enhance the bandwidth at the cost of a lowered absorption rate was investigated in [7].
Another popular method to widen the bandwidth is to introduce frequency-selective or reactive surfaces, the effects of which are usually modeled by simple equivalent circuits. This type of structure is usually called a circuit analog absorber [8ŌĆō18]. Circuit analog absorbers were also actively studied using equivalent circuits and optimizations usually combined with multiple-layer [8, 9] multiple-resonance [10ŌĆō12], or mixed [18] techniques, resulting in a significant bandwidth extension [12] up to 128% based on 90% absorption criteria. Some features of these developments are as follows.
A multi-layered structure with loaded chip resistors was proposed with an enhanced 99% absorption bandwidth of about 40 % [9]. A thin and broadband radar absorber using a resistive treble-square frequency selective surface consisting of three square loops was investigated in [10]. Its relative absorption bandwidth was 92.2% at the frequency range of 10.7ŌĆō29 GHz based on a 90% absorption rate. A triple-band planar absorber with a high-impedance surface was proposed with a theoretical derivation of a matching condition requiring varied resistance as a function of frequency [11]. The reported 90% absorption bandwidth is roughly 85% of the center frequency of 10 GHz, but it requires a mixture of different unit structures having different surface resistances per square. Using resistive trumpet-shaped structures coated on an FR-4 substrate, the metamaterial- inspired absorber for a wideband operation was proposed at the X-band [13]. Its 90% absorption bandwidth was 66.7% at 10.95 GHz. Clearly, by exploiting a large design space of multi-layers and element patterns, the incident angle of absorption, and the bandwidth can be maximized [8].
However, multi-layer structures may not be preferred in some environments because of the limitations of the thickness and the difficulties in fabrication. Therefore, many efforts are still being made to enhance the bandwidth assuming a single-layer design [12, 14ŌĆō17]. In [14], simple design equations for a wideband dipole-type absorber with complete absorption at a specific center frequency were presented, and a design example of a chip-resistor-loaded absorber was demonstrated. The chip-resistor-loaded absorber was later reported in [15, 19] as well. By employing discrete components, the thickness of the absorber can be shorter than a quarter wavelength while maintaining a relatively wide bandwidth. However, the issue of soldering many discrete components onto the circuit boards remains a drawback of this approach.
Without requiring discrete components and using a resistive silver nanowire (AgNW) film, a wideband X-band absorber employing a cross-shaped structure was presented in [16]. Its reported 90% absorption bandwidth with complete absorption at the design frequency of 10 GHz was about 80%. In [17], a thin resistive and capacitive absorber, which was composed of resistive rectangular structures using an AgNW film, was analyzed and evaluated at 3 GHz. It had a wideband absorption characteristic despite its relatively thin layer (a 90% absorption bandwidth of 76% with a layer thickness of only ╬╗/8 at 3 GHz).
This work determines a systematic method to widen the bandwidth of single-layered, circuit analog absorbers without soldering discrete components. In most cases, whether one uses multi-layer structures or circuit analog absorbers, a trade-off exists between the bandwidth and the absorption at the center frequency. In other words, at the expense of a lowered absorption rate, the bandwidth can increase. Although this sounds intuitively correct and has been demonstrated for Jaumann absorbers [7], the design guideline for single-layered circuit analog absorbers to balance between the bandwidth and the absorption rate has not been studied yet.
In this paper, we present simple, closed-form solutions for the design of single-layered wideband microwave absorbers with an arbitrary absorption rate at any design center frequency Žē
0. In Section II, the design equations are derived to maximize the flatness of reflection based on an equivalent circuit. Section III presents an easy guideline to finalize the dimensions of the used dipole structure without complicated optimization processes. In Section IV, a wideband microwave absorber at 10 GHz is designed and fabricated using the AgNW resistive film. The theoretical bandwidth of the presented absorber is compared with the measured one. The conclusion is given in Section V.
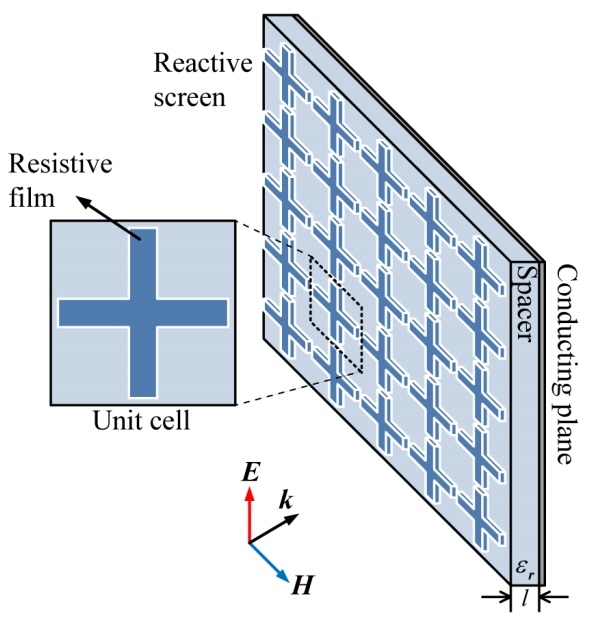
Fig. 1 shows the geometry of a typical microwave absorber using a reactive screen placed above a conducting plane [16, 17, 20]. The length of the spacer l is usually a quarter wavelength [4]. To realize a reactive screen, this work chooses a dipole-type structure. Specifically, a crossed-dipole pattern is chosen to make the absorption characteristics almost insensitive to the polarizations of incident electromagnetic waves, as will be seen in Section IV. The terminal impedance of the reactive screen can then be modelled as a lumped-series RLC resonator, as shown in Fig. 2. To optimize the pattern to have wideband absorption, we first analytically find the representative circuit values that should result in the maximum flatness of the reflection and wide bandwidth in this section. Based on the RLC values obtained from this section, the exact dimension of the pattern structure will be determined through electromagnetic (EM) simulations in Section III.
Fig. 2 shows the equivalent circuit composed of a series resonant circuit representing the reactive screen in the shunt branch and a quarter-wavelength transmission line that is terminated short. In Fig. 2, ╬Ę
0 (=377 ╬®) and ╬Ę
1 are the intrinsic impedances of free space and the spacer, respectively, and Z
0 is the impedance of the resonant circuit consisting of R
0, L
0, and C
0. With a quarter-wavelength spacer l, the electrical length ╬▓l is ŽĆ/2 at the design center frequency Žē
0. L
0 and C
0 are chosen to resonate at the design center frequency Žē
0 in this work.
The input admittance Y
in
at the front of the screen is
where
Žē 0 L 0 = L 0 / C 0
and
The idea of a traditional, purely resistive Salisbury screen is to use Z
0 = ╬Ę
0 = 377 ╬®, and thus match Y
in
(Žē) = 1/╬Ę
0 at the design center frequency Žē = Žē
0. This results in perfect absorption A(Žē
0) = A
0 = 1 at the center frequency, but the bandwidth is relatively narrow.
[7] suggests that the bandwidth can be increased further by introducing a slight mismatch at the center frequency. To quantify this effect, we introduce a match factor m given by
The absorption A
0 at the center frequency now deviates from unity as
For a specifically desired absorption A
0, the match factor m can either be
or
When the required absorption A
0 is unity, we have m
1 = m
2 = 1. However, when a slight mismatch is introduced, we have two options to determine R
0; m
1 < 1 and m
2 > 1.
L
0 and C
0 can be determined to enhance the bandwidth. Reminiscent of how the Butterworth filter has a maximum flat response [21], the bandwidth can be widened by enforcing
for as large an n as possible. Intuitively, if (8) is satisfied for every non-negative integer n, ╬ō is simply zero for an infinite bandwidth. In this work, we have only one independent energy storage element L
0. Once L
0 is determined, C
0 is determined accordingly to resonate with L
0 at the design center frequency Žē
0. With one independent energy storage element, the number of derivatives that can be set to zero in (8) is at most one in general. The condition of
d | ╬ō ( Žē ) | 2 d Žē | Žē = Žē 0 = 0
Moreover, if (9) is satisfied, as |╬ō(Žē)| must be close to zero in any practical absorber design, the second derivative in (8) will automatically be largely satisfied (refer to the Appendix for the derivation). This assures the design to have the maximum flatness of the response with a limited number of independent energy storage elements.
Certainly, the maximum flatness of the reflection at the design center frequency does not necessarily imply maximum bandwidth for arbitrary criteria, such as 99% or 90%. Intuitively, the maximum flatness condition is more similar to the maximum bandwidth condition for wideband absorption, such as 99 % bandwidth, than that to low ones. Nevertheless, regardless of specific bandwidth criteria, this is a good starting point before further optimization. Therefore, for wideband absorption, we first look for the values of L
0 and C
0 that yield maximum flatness, satisfying (9).
Eq. (9) implies that the derivative of both the input conductance G
in
and the input susceptance B
in
should be zero at Žē = Žē
0. From the expression in (1), the derivative of the input conductance G
in
is zero at Žē = Žē
0. Therefore, the requirements for L
0 and C
0 are obtained from the condition
d B i n ( Žē ) d Žē | Žē = Žē 0 = 0
The derivative of B
in
is given by
Equating (10) to zero at Žē = Žē
0 yields L
0 and C
0 as
and
the values of which are determined according to a desired match factor m.
To investigate which match factor among m
1 and m
2 is a better choice, the circuit simulation of B
in
in Fig. 2 is run, and the results are compared.
When A
0 = 0.9 for example, the match factor can either be m
1 = 0.5195 or m
2 = 1.925. For each case, we have an (R
0, Žē
0
L
0) of (196 ╬®, 80 ╬®) and (725.2 ╬®, 1,096.4 ╬®), respectively. Fig. 3 shows the susceptances of the reactive screen B
0, short-terminated quarter-wavelength transmission line B
1, and their sum B
in
for these two cases. Clearly, for both cases, the susceptance and its slope are zero at the design center frequency, as expected.
Conversely, the choice of m
1 in Fig. 3(a) leads to a wider resonant bandwidth than the choice of m
2 in Fig. 3(b). The reason is that the two zero-derivatives of B
0 are farther apart with m
1 than with m
2. For example, in Fig. 3, the distance between the two zero-derivatives of B
0 is about 1.5Žē
0 (= 1.9Žē
0 ŌłÆ 0.4Žē
0) for m
1, which is much greater than 0.45Žē
0 (= 1.3Žē
0 ŌłÆ 0.85Žē
0) for m
2. From (10), it is straightforward to show that this holds generally true for any choice of absorption A
0; i.e., the zero-derivatives of B
0 are split farther apart for smaller match factors. The wide resonant bandwidth of B
in
naturally broadens the absorption bandwidth. Therefore, in this work, the smaller match factor m
1 of (6) is chosen to determine R
0, L
0, and C
0 in an effort to enhance the absorption bandwidth.
We now evaluate the effect of the maximum flatness design on the absorption bandwidth. Fig. 4(a)ŌĆō(b) show the input impedance and absorption as a function of the normalized frequency obtained from the Agilent ADS circuit simulation in Fig. 2. The results of the purely resistive Salisbury screen and those of the proposed reactive Salisbury screens with A
0 = 1 and 0.9 are compared. For simplicity, the relative permittivity of the spacer layer is assumed to be unity. The used circuit components (R
0, Žē
0
L
0) of the resistive Salisbury screen, the reactive one with A
0 = 1, and the reactive one with A
0 = 0.9 are (377 ╬®, 0 ╬®), (377 ╬®, 296 ╬®), and (196 ╬®, 80 ╬®), respectively.
In Fig. 4(a), the reactance of the reactive absorbers is zero over a wide bandwidth region near the design center frequency. This property, which the purely resistive Salisbury screen does not possess, endows the absorber with a much wider bandwidth, as shown in Fig. 4(b). Furthermore, a wider flatness both in the resistance and the reactance near the design frequency is observed when sacrificing absorption at the center frequency from A
0 = 1 to A
0 = 0.9, as shown in Fig. 4(a). As a result, when A
0 = 0.9, the 90% absorption bandwidth reaches up to 119% from 0.35Žē
0 to 1.54Žē
0 (Fig. 4(b)).
If necessary, the adjustments for L
0 and C
0 can be made to further enhance the bandwidth according to specific bandwidth criteria. For example, let us assume that we are interested in maximizing the 90% absorption bandwidth. In Fig. 4(b), the maximum flatness design of A
0 = 0.9 suffers asymmetry around the design center frequency Žē
0. This scenario is better visualized using the Smith chart in Fig. 4(c). The reflection coefficient ╬ō of the maximum flatness design quickly moves to the short impedance above the design center frequency. This results in the absorption bandwidth being considerably narrow in the upper range, Žē
0ŌĆō1.54Žē
0, compared with 0.35Žē
0ŌĆōŽē
0 in the lower range.
An effective way to increase the upper bandwidth is to slightly increase the inductive reactance Žē
0
L
0, creating an additional resonant frequency beyond the design center frequency, as shown in the solid curve in Fig. 4(c). The appearance of an additional resonant frequency is not a coincidence. The maximum flatness design places multiple roots of the resonance at the design center frequency Žē
0 because
B i n ( Žē 0 ) = d d Žē B i n ( Žē ) | Žē = Žē 0 = 0 Žē 0 = 1 / L 0 C 0
Let us summarize the method of obtaining the required circuit components representing the reactive screen. If a specific A
0 is desired at Žē
0, the match factor m
1 < 1 is obtained using (6). Then R
0, L
0, and C
0 are first determined to maximize the flatness of the reflection at the design center frequency following (4), (11), and (12). The maximum flatness essentially widens the bandwidth of the absorption. To increase the bandwidth specifically for certain criteria, L
0 and C
0 can be tuned to maximize the bandwidth through circuit simulation while maintaining
Žē 0 = 1 / L 0 C 0
The design procedures explained in Section II are scalable to any frequency in general. In this work, we build an absorber around the center frequency of 10 GHz.
We physically realize the circuit parameters obtained in Section II with the crossed-dipole structure. In Fig. 6(a), a is the side length of the absorber square unit, w and h are the width and height of the crossed-dipole made of a resistive film, respectively, R
s
is the resistance per square of the film material, and g is the gap distance.
The terminal impedance on the resistive film is a function of the structure dimension. Clearly, the series circuit components R
0, L
0, and C
0 of the unit cell are monotonous functions of R
s
h/w, h/w, and w/g, respectively. Therefore, finding a dimension to synthesize the required circuit components requires only a few iterations of electromagnetic simulations. In other words, by separating the work of optimization and realization each done by the circuit and electromagnetic simulations, the design process of the structure is less expensive in terms of computation than other optimization approaches, which heavily rely on electromagnetic simulations [13, 19, 20].
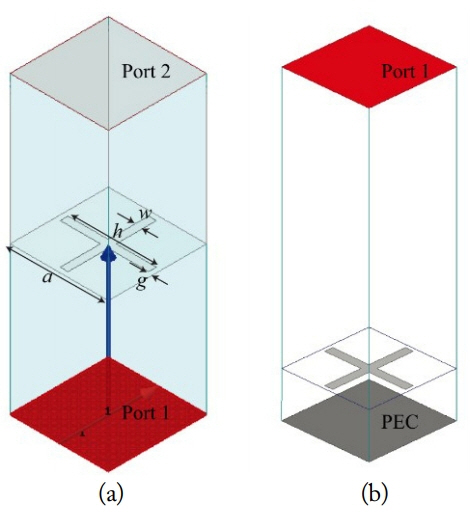
To evaluate the terminal impedance, a two-port simulation is run in Ansys HFSS with de-embedding of the effect of finite distances between the ports and the film, as shown in Fig. 6(a). Through this simulation, the dimensions of the unit structure that realize the required circuits values in Table 1 are found and tabulated in the same table.
The simulated absorption using HFSS is also straightforward, as shown in Fig. 6(b). A perfect electric conductor is placed at a quarter-wavelength distance behind the pattern. For example, when an air medium is used as a spacer, the absorption of the crossed-dipole structures in Table 1 is simulated in HFSS and compared with those of the corresponding circuits in Fig. 7. As the terminal impedance is well synthesized by the pattern structure (although not included in this work), the absorption of the maximum flatness designs from HFSS successfully reproduces the circuit behaviors.
Additionally, a comparison between the absorber proposed here and those reported in the literatures is presented in Table 2. Our design methodology based on the maximum flatness of the equivalent circuit design is mathematically straightforward and requires neither many iterative electromagnetic simulations nor the soldering of external components. Nevertheless, it provides quality performance in terms of the bandwidth compared with other published works.
For the purpose of demonstration, the crossed-dipole absorber with the required absorption of A
0 = 1 at the design center frequency of 10 GHz is fabricated and measured.
The AgNW film with 30 ╬®/square is used for a resistive sheet. AgNWs are chosen for fabrication because their sheet resistance can be easily controlled by adjusting the concentration of the AgNW solution [23]. Fig. 8 shows the geometry of the unit cell for the fabricated absorber. Owing to the difficulty of applying and laser-cutting the film directly on to a Styrofoam spacer with ╔ø
r
= 1.03, we first attached the film on an acrylic layer with ╔ø
r
= 2.56, which was later mounted on the Styrofoam layer. The acrylic layer with a thickness l
1 of 1.5 mm was used. The thickness of the Styrofoam l
2 was determined to be 4 mm to ensure a zero susceptance of Y
1 at 10 GHz. Based on the same condition, the effective permittivity ╔ø
eff
and the intrinsic impedance ╬Ę
1 of an effective single-layer spacer were 1.86 and 276.5 ╬®, respectively.
With m = 1, ╬Ę
0 = 377 ╬®, and ╬Ę
1 = 276.5 ╬®, the circuit values for the maximum flatness were (R
0, L
0, C
0) = (377 ╬®, 6.42 nH, 39.5 fF). The fine adjustments of L
0 and C
0 for further bandwidth enhancement were omitted in this fabrication example. After all, the dimensions of the unit structure to realize the above circuit values were determined through electromagnetic simulations and are summarized in Table 3.
The input impedance Z
in
of the structure in Table 3 was first simulated using HFSS in Fig. 9(a) and then compared with the input impedance of the circuits in Fig. 2 with (R
0, L
0, C
0) = (377 ╬®, 6.42 nH, 39.5 fF) for the maximum flatness. The crossed-dipole structure realized the impedances for the maximum flatness across a wide frequency range. Therefore, the absorption of the crossed-dipole structure was also in good agreement with that of the circuit in Fig. 9(b), showing the wide bandwidth. The EM-simulated 99% and 90% absorption bandwidths were about 42.7% and 78.1%, respectively.
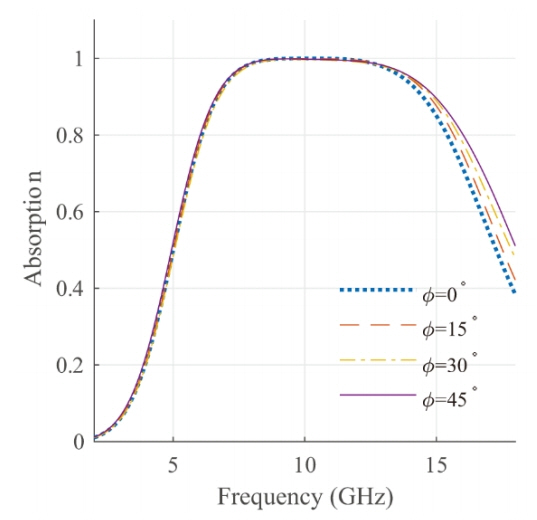
We also considered a normal incidence case with different polarization angles Žå. Fig. 10 shows the electromagnetically simulated absorptions depending on the polarization angles of the normally incident electric fields from 0┬░ to 45┬░. The polarization angle exhibited negligible effects on the absorption due to the employed crossed-dipole structure. For the degradation effects with oblique TE and TM incidence cases, we can apply similar techniques given in [8], but these are not included in this work.
Fig. 11(a) shows the photograph of the fabricated absorber, which was made of the AgNW resistive film, acryl, Styrofoam, and conducting plane. The absorber consisted of 25 ├Ś 17 units, and the overall size was 270.5 mm ├Ś 183.9 mm ├Ś 4.5 mm. The experimental setup is illustrated in Fig. 11(b). The absorption was measured by the horn antenna of Model 3117 (1ŌĆō18 GHz) produced by ETS Lindgren Inc.
Fig. 12 shows the circuit simulation, the EM simulation, and the measurement of the absorption of the proposed screen with a design center frequency of 10 GHz. The measured absorption was obtained by estimating |S
11|2 on the absorber plane based on the reflection coefficient measured by the horn antenna. In the measurement, only the reflection on the absorber plane was considered, not the horn antenna itself. To calibrate the self-reflection of the horn antenna, the horn antenna in free space is used as the match load in the calibration process instead of the typical 50 ╬® load. In addition, the reflection coefficient in front of the reversed absorber with the same size as the absorber is used as the reference to compensate for the energy leakage through the space. A more detailed measurement method using a single antenna can be referenced in [13]. For example, the 90% absorption bandwidths of each one are 75.7%, 78.1%, and 66.4%, respectively. The difference between the simulation and the measurement could be attributed to the non-uniformity of the resistivity in the AgNW film and the limited size of the absorber in the measurement.
Based on the requirements of a maximum flat reflection at a design center frequency, a simple closed-form design solution of a reactive Salisbury screen has been derived. Having maximum flatness widens the bandwidth. For example, for the desired absorptions of 100%, 99%, and 90% at a design center frequency, the 90% bandwidths can be widened to 89%, 105%, and 119%, respectively, from 74% for a traditional Salisbury screen. Furthermore, to maximize the bandwidth with specific criteria, further numerical optimization can be made by tuning the circuit parameters, starting from the maximum flatness condition.
For fabrication and measurement, an absorber with a design center frequency of 10 GHz was designed and fabricated using the AgNW resistive film with a surface resistance of 30 ╬®/square. The measured absorption showed a good agreement with the simulation results, validating the effectiveness of the proposed design procedures.
Acknowledgments
This work was supported by the Institute for Information & Communications Technology Promotion (IITP) grant funded by the Korea government (MSIT) (No. IITP-2018-2016-0-00291, Information Technology Research Center).
Fig.┬Ā3
Choice of match factor. Susceptances of the reactive screen B
0, short-terminated quarter-wavelength transmission line B
1, and their sum B
in
= B
0 + B
1 when A
0 = 0.9 as a function of normalized frequency for the cases of (a) m
1 = 0.5195 and (b) m
2 = 1.925.
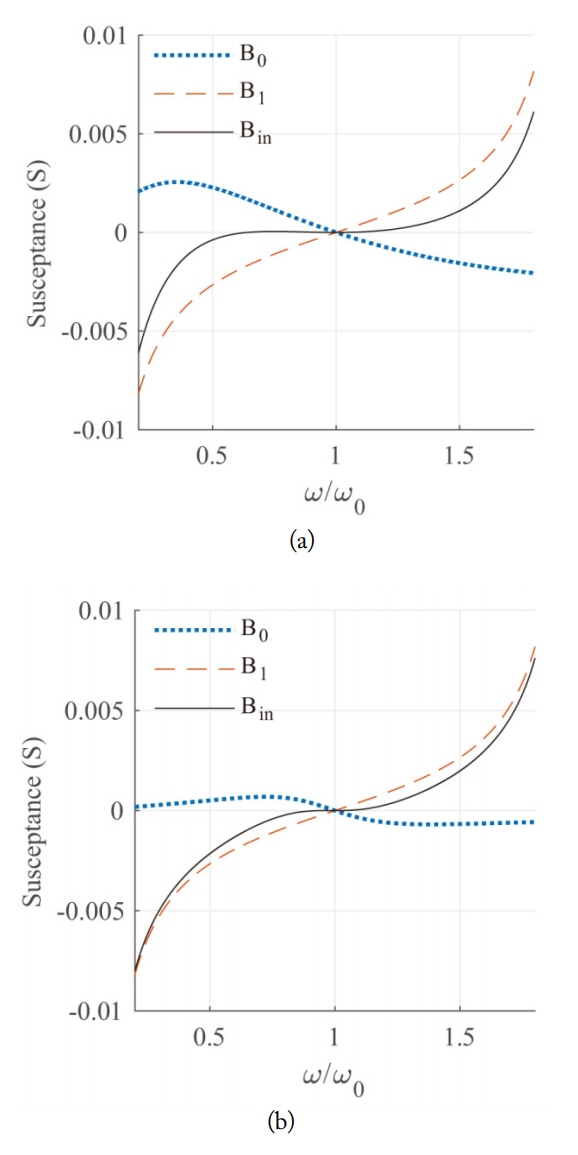
Fig.┬Ā4
(a) Input impedances and (b) absorption of the air-spaced absorber as a function of normalized frequency. The (R
0, Žē
0
L
0) for each absorber are as follows: resistive Salisbury (377 ╬®, 0 ╬®), maximum flatness with A
0 = 1: (377 ╬®, 296 ╬®), maximum flatness with A
0 = 0.9 (196 ╬®, 80 ╬®), and final adjustment for 90% criteria (196 ╬®, 120 ╬®). (c) The Smith chart showing the reflection coefficients of each design. All of the traces rotate clockwise with the frequency. The markers on the traces represent the frequencies of 0.6Žē
0, Žē
0, and 1.4Žē
0 in order.

Fig.┬Ā5
Absorption bandwidth with varying inductive reactance Žē
0
L
0. The 90% bandwidth is 119%, 123%, 124%, and 123% when Žē
0
L
0 is 80 ╬®, 100 ╬®, 120 ╬®, and 140 ╬®, respectively.
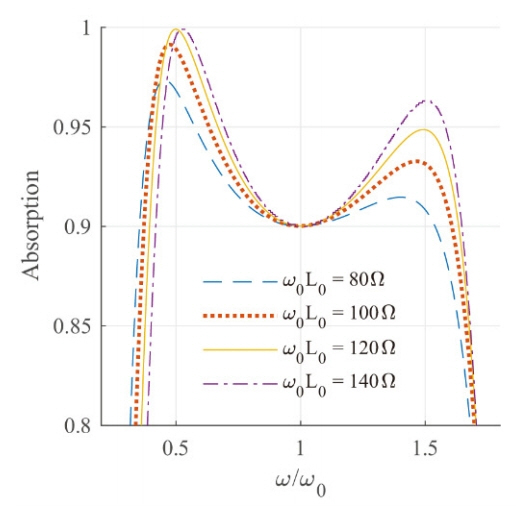
Fig.┬Ā7
Absorption of air-spaced maximum flatness design: circuit (dashed line) and electromagnetic (solid line) simulations.
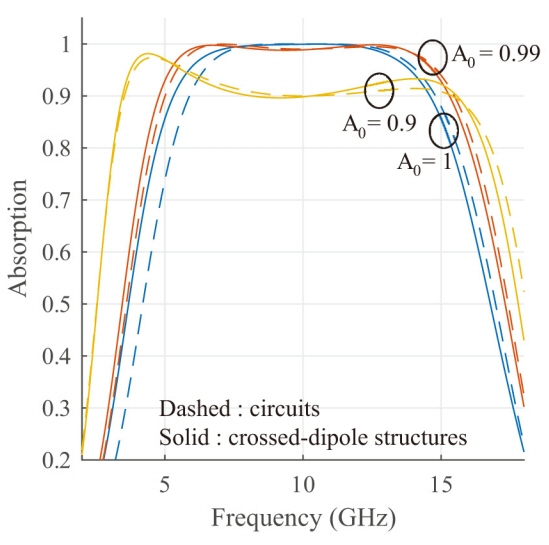
Fig.┬Ā8
Geometry of a unit structure for the fabricated absorber employing a crossed-dipole structure.
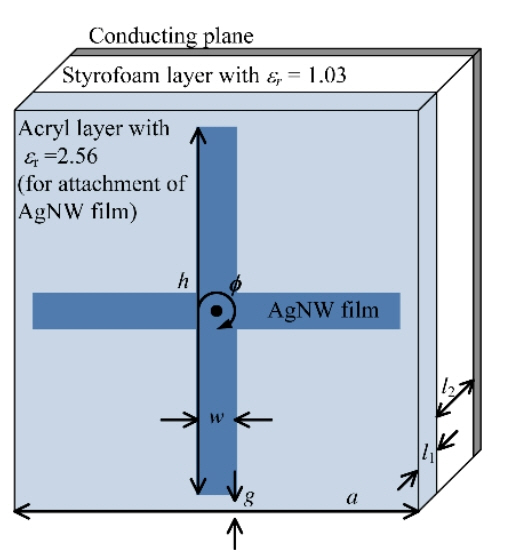
Fig.┬Ā9
(a) Input impedance and (b) absorption of a unit of the reactive screen employing a crossed-dipole structure when A
0 = 1 (solid lines). They synthesize the circuits with a maximum flatness impedance (R
0, L
0, C
0) = (377 ╬®, 6.42 nH, 39.5 fF) (dashed lines).

Fig.┬Ā11
Photograph of (a) the fabricated proposed reactive screen realized on an acrylic layer and (b) the experimental setup. The inset of (a) shows the closed view of the crossed-dipole structure.

Table┬Ā1
Circuit parameters and their 90% absorption bandwidths from circuit simulation
Table┬Ā2
Bandwidth and thickness comparison of the reported single- layer absorber structures
| Ref. | Bandwidth (%) | Thickness (╬╗ 0) | Unit cell |
|---|---|---|---|
| [12] | 98.4 | 0.25 | Resistive square patch |
| [22] | 81.7 | 0.13 | Hexagonal with resistors |
| [15] | 70.7 | 0.12 | Crossed-dipole with resistors |
| [16] | 80 | 0.25 | Crossed-shaped resistive film |
| [17] | 76 | 0.125 | Square-shaped resistive film |
| [20] | 117 | 0.2 | Hexagonal with film surface |
| [19] | 105 | 0.128 | Dipole antenna with resistors |
| This work | 124 | 0.25 | Crossed-dipole resistive film |
References
1. H Li, LH Yuan, B Zhou, XP Shen, Q Cheng, and TJ Cui, "Ultrathin multiband gigahertz metamaterial absorbers," Journal of Applied Physics, vol. 110, article no. 014909, 2011.

2. J Lee, M Yoo, and S Lim, "A study of ultra-thin single layer frequency selective surface microwave absorbers with three different bandwidths using double resonance," IEEE Transactions on Antennas and Propagation, vol. 63, no. 1, pp. 221ŌĆō230, 2015.

3. F Costa, S Genovesi, A Monorchio, and G Manara, "A circuit-based model for the interpretation of perfect metamaterial absorbers," IEEE Transactions on Antennas and Propagation, vol. 61, no. 3, pp. 1201ŌĆō1209, 2013.

4. WW Salisbury, "Absorbent body for electromagnetic waves," US Patent, 2599944A. June 10 1952.
5. RL Fante and MT McCormack, "Reflection properties of the Salisbury screen," IEEE Transactions on Antennas and Propagation, vol. 36, no. 10, pp. 1443ŌĆō1454, 1988.

6. BA Munk, Frequency Selective Surfaces, Theory and Design. New York, NY: Wiley, 2000.
7. B Chambers, "Optimum design of a Salisbury screen radar absorber," Electronics Letters, vol. 30, no. 16, pp. 1353ŌĆō1354, 1994.

8. BA Munk, P Munk, and J Pryor, "On designing Jaumann and circuit analog absorbers (CA Absorbers) for oblique angle of incidence," IEEE Transactions on Antennas and Propagation, vol. 55, no. 1, pp. 186ŌĆō193, 2007.

9. AP Sohrab and Z Atlasbaf, "A circuit analog absorber with optimum thickness and response in X-band," IEEE Antennas and Wireless Propagation Letters, vol. 12, pp. 276ŌĆō279, 2013.

10. M Li, S Xiao, YY Bai, and BZ Wang, "An ultrathin and broadband radar absorber using resistive FSS," IEEE Antennas and Wireless Propagation Letters, vol. 11, pp. 748ŌĆō751, 2012.

11. GR Zhang, PH Zhou, HB Zhang, LB Zhang, JL Xie, and LJ Deng, "Analysis and design of triple-band high-impedance surface absorber with periodic diversified impedance," Journal of Applied Physics, vol. 114, article no. 164103, 2013.

12. Y Shang, Z Shen, and S Xiao, "On the design of single-layer circuit analog absorber using double-square-loop array," IEEE Transactions on Antennas and Propagation, vol. 61, no. 12, pp. 6022ŌĆō6029, 2013.

13. BK Kim and B Lee, "Wideband absorber at X-band adopting trumpet-shaped structures," Electronics Letters, vol. 50, no. 25, pp. 1957ŌĆō1959, 2014.

14. G Kim and B Lee, "Design of wideband absorbers using RLC screen," Electronics Letters, vol. 51, no. 11, pp. 834ŌĆō836, 2015.

15. D Kundu, A Mohan, and A Chakrabarty, "Single-layer wideband microwave absorber using array of crossed dipoles," IEEE Antennas and Wireless Propagation Letters, vol. 15, pp. 1589ŌĆō1592, 2016.

16. J Lee and B Lee, "Wideband absorber using silver nanowire resistive film," Electronics Letters, vol. 52, no. 8, pp. 631ŌĆō633, 2016.

17. J Lee and B Lee, "Design of thin RC absorbers using a silver nanowire resistive screen,ŌĆØ," Journal of Electromagnetic Engineering and Science, vol. 16, no. 2, pp. 106ŌĆō111, 2016.

18. Y Han, W Che, C Christopoulos, Y Xiong, and Y Chang, "A fast and efficient design method for circuit analog absorbers consisting of resistive square-l op arrays," IEEE Transactions on Electromagnetic Compatibility, vol. 58, no. 3, pp. 747ŌĆō757, 2016.

19. XQ Lin, P Mei, PC Zhang, ZZD Chen, and Y Fan, "Development of a resistor-loaded ultrawideband absorber with antenna reciprocity," IEEE Transactions on Antennas and Propagation, vol. 64, no. 11, pp. 4910ŌĆō4913, 2016.

20. J Chen, Z Hu, GD Wang, X Huang, S Wang, X Hu, and M Liu, "High-impedance surface-based broadband absorber with interference theory," IEEE Transactions on Antennas and Propagation, vol. 63, no. 10, pp. 4367ŌĆō4374, 2015.

21. TH Lee, Planar Microwave Engineering: A Practical Guide to Theory, Measurement, and Circuits. Cambridge: Cambridge University Press, 2004.
Appendices
Appendix
For the maximum flatness of |╬ō(Žē)|2 at Žē = Žē
0, we require
and
where ╬ō(Žē
0) = G
╬ō(Žē
0) + jB
╬ō(Žē
0), and the parameter Žē
0 is omitted for simplicity of the expression. Note that if we have both ╬ō(Žē
0) = 0 and ╬ōŌĆ▓(Žē
0) = 0, then (A1) and (A2) are satisfied.
To satisfy ╬ōŌĆ▓(Žē
0) = 0, from (2), we have
Therefore, the choice of L
0 and C
0 to make
d Y i n ( Žē ) d Žē = 0
Biography
Gunyoung Kim received his B.S. degree in radio communication engineering from Kyung Hee University, Yongin, Korea, in 2010 and his M.S. degree in electronics and radio engineering from Kyung Hee University in 2012. He is currently working toward his Ph.D. degree in electronics and radio engineering at the same university. His fields of research include microwave antennas, passive devices, wireless power transmission, and metamaterials.

Biography
Sanghoek Kim received his B.S. degree with a double major in electrical engineering and mathematics from Seoul National University, Seoul, Korea, in 2007, and his M.S. and Ph.D. degrees in electrical engineering from Stanford University, CA, USA, in 2013. His research focuses on the applications of radio-frequency technology and electromagnetics theory in wireless power transfer, communications, and signal integrity in high-speed channels. After graduation, he worked at Qualcomm Inc., as a signal/power integrity engineer and in SiBeam Inc., as an mmWave system engineer. Currently, he is an assistant professor in the Department of Electronics and Radio Engineering at Kyung Hee University.

Biography
Bomson Lee received his B.S. degree in electrical engineering from Seoul National University, Seoul, Korea, in 1982. From 1982 to 1988, he worked at Hyundai Engineering Company Ltd., Seoul, Korea. He received his M.S. and Ph.D. degrees in electrical engineering from the University of Nebraska, Lincoln, NE, USA, in 1991 and 1995, respectively. In 1995, he joined the faculty at Kyung Hee University, where he is currently a professor in the Department of Electronics and Radio Engineering. From 2007 to 2008, he was the chair of the technical group for microwave and radio wave propagation in the Korea Institute of Electromagnetic Engineering & Science (KIEES). In 2010, he was the editor-in-chief of the Journal of the Korean Institute of Electromagnetic Engineering and Science. From 2015 to 2016, he served as a vice chairman in KIEES. In 2017, he was an executive vice chairman in KIEES. Since 2018, he has been the president of KIEES. He was the president of KIEES in 2018. His research activities include microwave antennas, RF identification tags, microwave passive devices, wireless power transfer, and metamaterials.

- TOOLS